그래프 (Graph)

BrokenFinger98·2024년 8월 23일

Graph Problem Solving

Problem Solving

목록 보기

15/29

그래프

그래프는 아이템(사물 또는 추상적 개념)들과 이들 사이의 연결 관계를 표현한다.
정점(Vertex) : 그래프의 구성요소르 하나의 연결점
간선(Edge) : 두 정점을 연결하는 선
차수(Degree) : 정점에 연결된 간선의 수
그래프는 정점(Vertex)들의 집합과 이들을 연결하는 간선(Edge)들의 집합으로 구성된 자료 구조
V: 정점의 개수, E: 그래프에 포함된 간선의 개수
V개의 정점을 가지는 무방향 그래프는 최대 V(V-1)/2 간선이 가능
예) 5개의 정점이 있는 무방향 그래프의 최대 간선 수는 10(=>54/2)개이다.
선형 자료구조나 트리 자료구조로 표현하기 어려운 N : N 관계를 가지는 원소들을 표현하기에 용이하다.

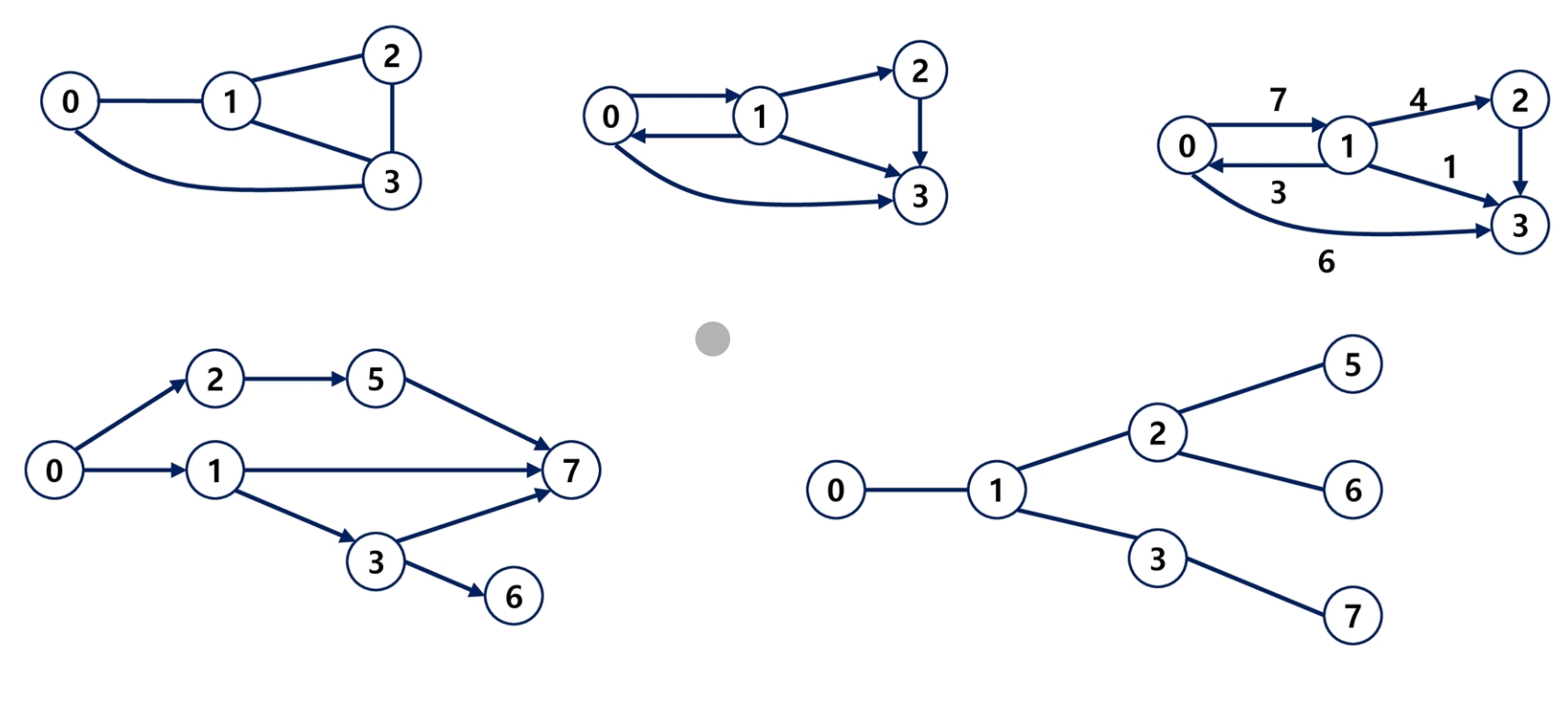
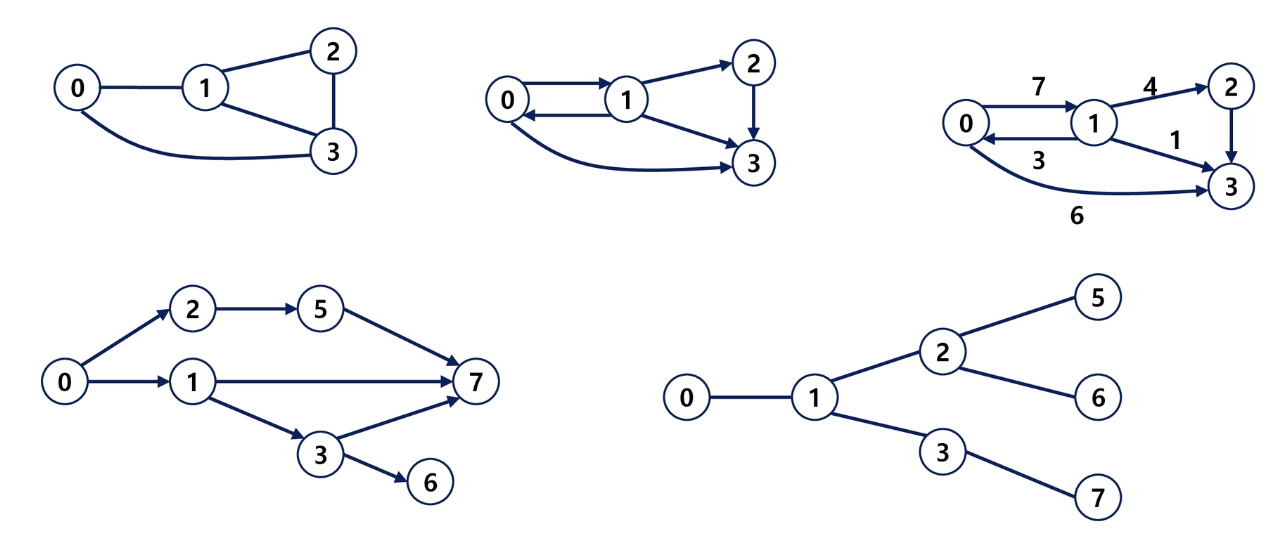
그래프 유형

무방향 그래프(Undirected Graph)
방향 그래프(Directed Graph)
가중치 그래프(Weighted Graph)
사이클이 없는 방향 그래프(DAG, Directed Acyclic Graph)

완전 그래프
정점들에 대해 가능한 모든 간선들을 가진 그래프
부분 그래프
원래 그래프에서 일부의 정점이나 간선을 제외한 그래프
트리도 그래프이다
- 각 노드는 최대 하나의 부모 노드가 존재할 수 있다.
- 각 노드는 자식 노드가 없거나 하나 이상이 존재할 수 있다.
- 두 노드 사이에는 유일한 경로가 존재한다.

인접 정점

인접(Adjacency)

두 개의 정점에 간선이 존재(연결됨)하면 서로 인접해 있다고 한다.
완전 그래프에 속한 임의의 두 정점들은 서로 인접해 있다.

그래프 경로

경로(Path)란 어떤 정점 A에서 시작하여 다른 정점 B로 끝나는 순회를 두 정점 사이를 잇는 간선들을 순서대로 나열한 것
- 같은 정점을 거치지 않은 간선들의 sequence
- 어떤 정점에서 다른 정점으로 가는 경로는 여러가지일 수 있다.
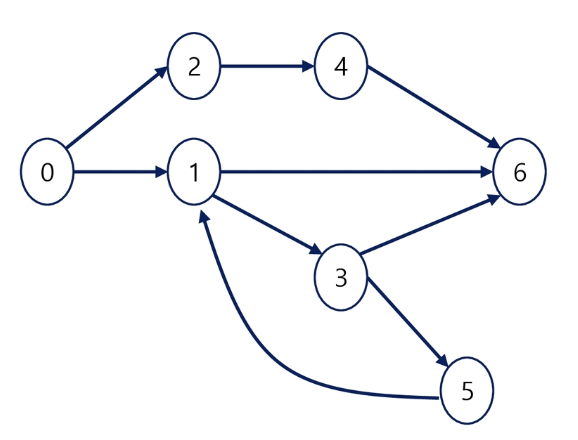
- 0 - 6의 경로 예시
  - 정점들: 0 - 2 - 4 - 6
  - 간선들: (0, 2), (2, 4), (4, 6)

싸이클(Cycle)

경로의 시작 정점과 끝 정점이 같음
시작한 정점에서 끝나는 경로
1 - 3 - 5 -1

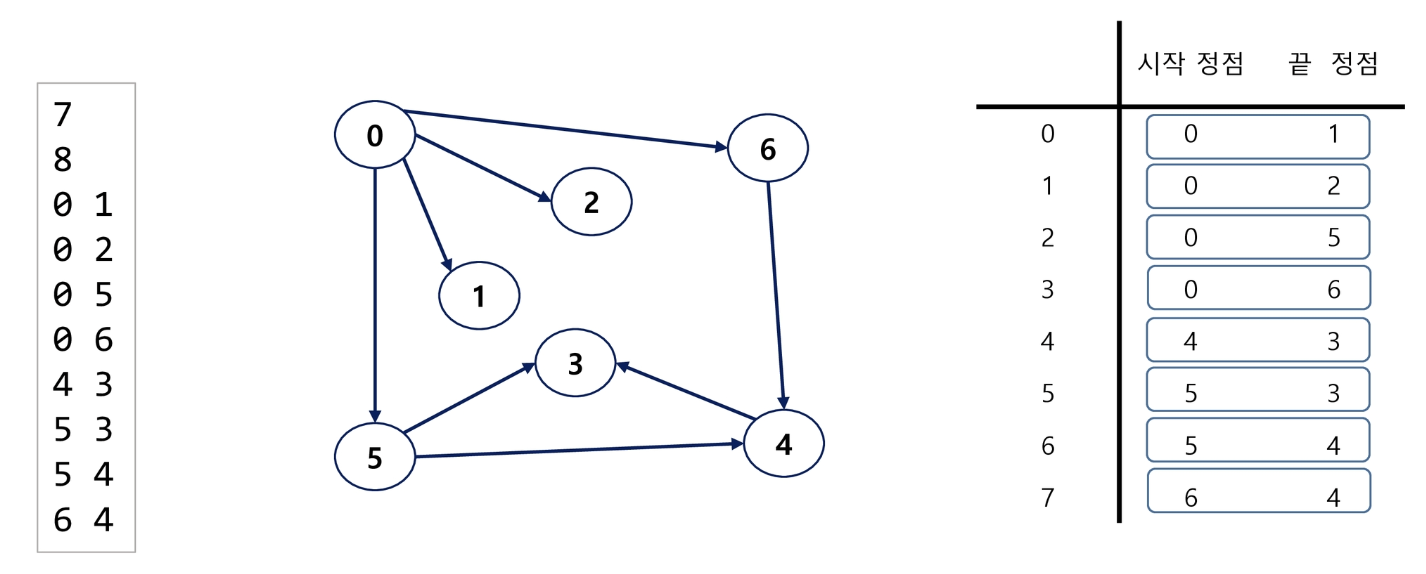
그래프 표현

간선의 정보를 저장하는 방식, 메모리나 성능을 고려해서 결정
인접 행렬(Adjacent matrix)
- V x V 크기의 2차원 배열을 이용해서 간선 정보를 저장
- 배열의 배열
인접 리스트(Adjacent List)
- 각 정점마다 다른 정점으로 나가는 간선의 정보를 저장
간선 리스트(Edge List)
- 간선(시작 정점, 끝 정점)의 정보를 객체로 표현하여 리스트에 저장

인접 행렬

두 정점을 연결하는 간선의 유무를 행렬로 표현
- V x V 정방 행렬
- 행 번호와 열 번호는 그래프의 정점에 대응
- 두 정점이 인접되어 있으면 1, 그렇지 않으면 0으로 표현
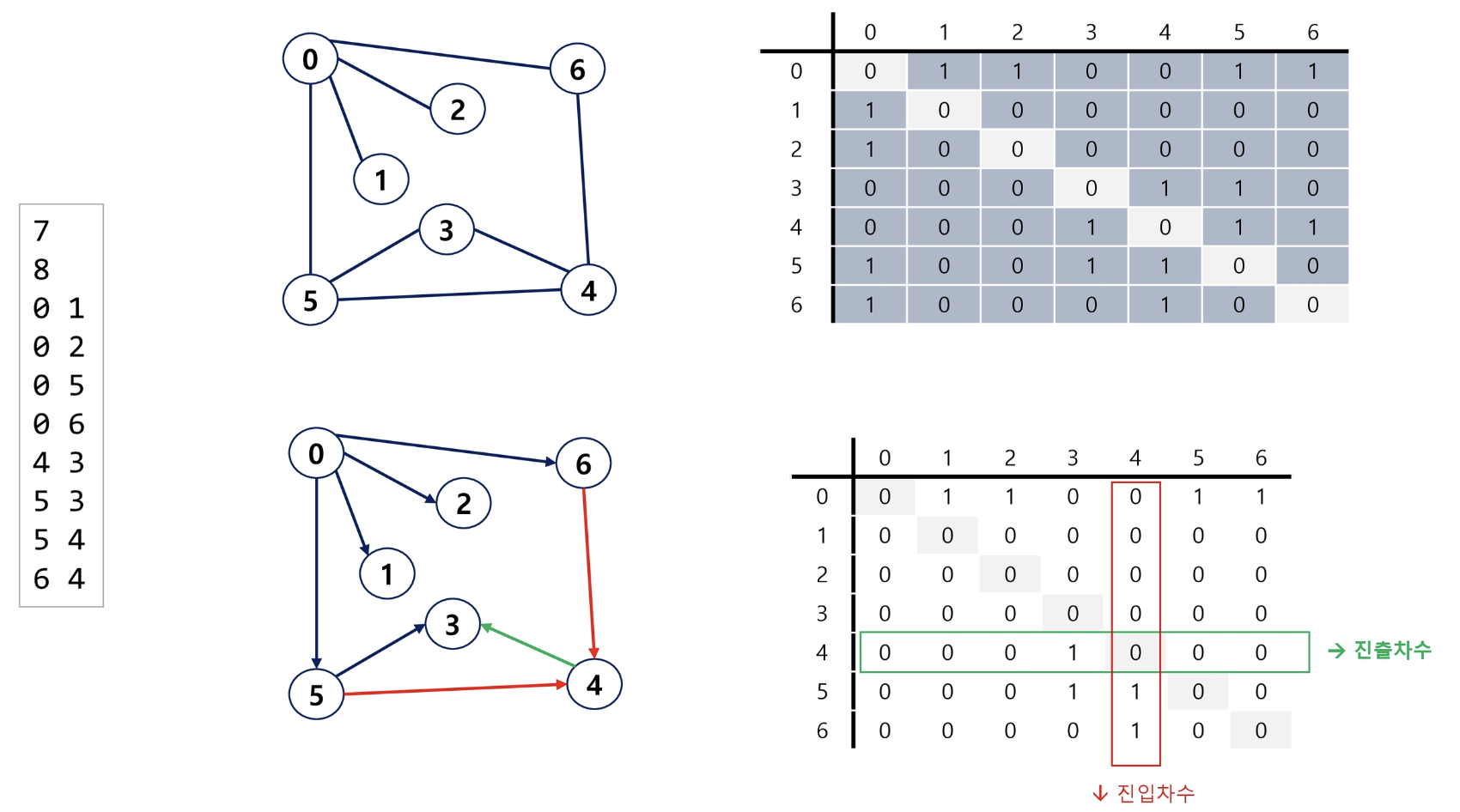
무방향 그래프
- i번째 행의 합 = i번째 열의 합 = Vi의 차수
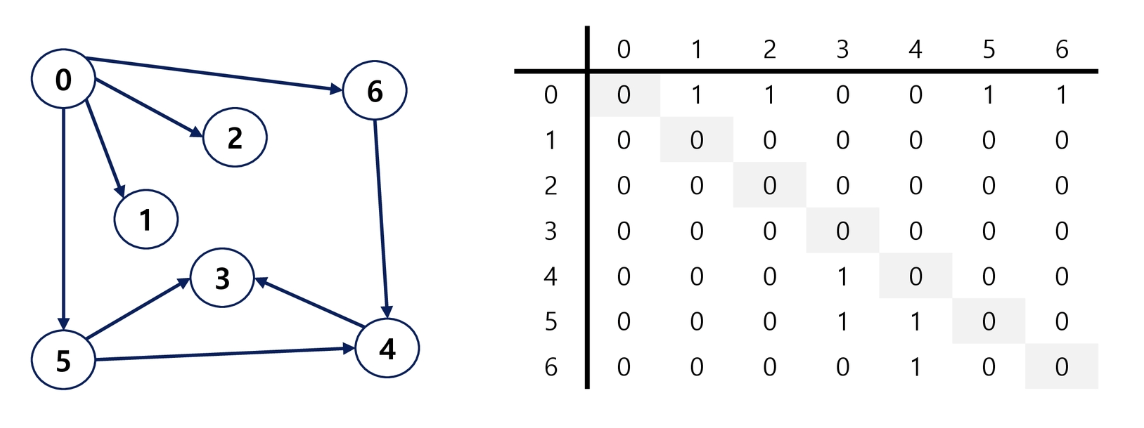
방향 그래프
- 행 i의 합 = Vi의 진출 차수
- 열 i의 합 = Vi의 진입 차수

인접 행렬의 단점은?
희소 그래프(Sparse Graph) VS 밀집 그래프(Dense Graph)

import java.util.Arrays;
import java.util.Scanner;

public class AdjMatrixTest {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int V = sc.nextInt();       // 정점 개수
        int E = sc.nextInt();       // 간선 개수

        // 무방향 그래프
        int[][] adjMatrix = new int[V][V]; // 기본 초기화값 0 : 인접하지 않은 상태
        for (int i = 0; i < E; i++) {
            int from = sc.nextInt();
            int to = sc.nextInt();
            adjMatrix[to][from] = adjMatrix[from][to] = 1;
        }
        for (int[] adj : adjMatrix) {
            System.out.println(Arrays.toString(adj));
        }
    }
}
/*
입력
7
8
0 1
0 2
0 5
0 6
4 3
5 3
5 4
6 4
 */
/*
출력
[0, 1, 1, 0, 0, 1, 1]
[1, 0, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 1, 1, 0]
[0, 0, 0, 1, 0, 1, 1]
[1, 0, 0, 1, 1, 0, 0]
[1, 0, 0, 0, 1, 0, 0]
 */

인접 리스트

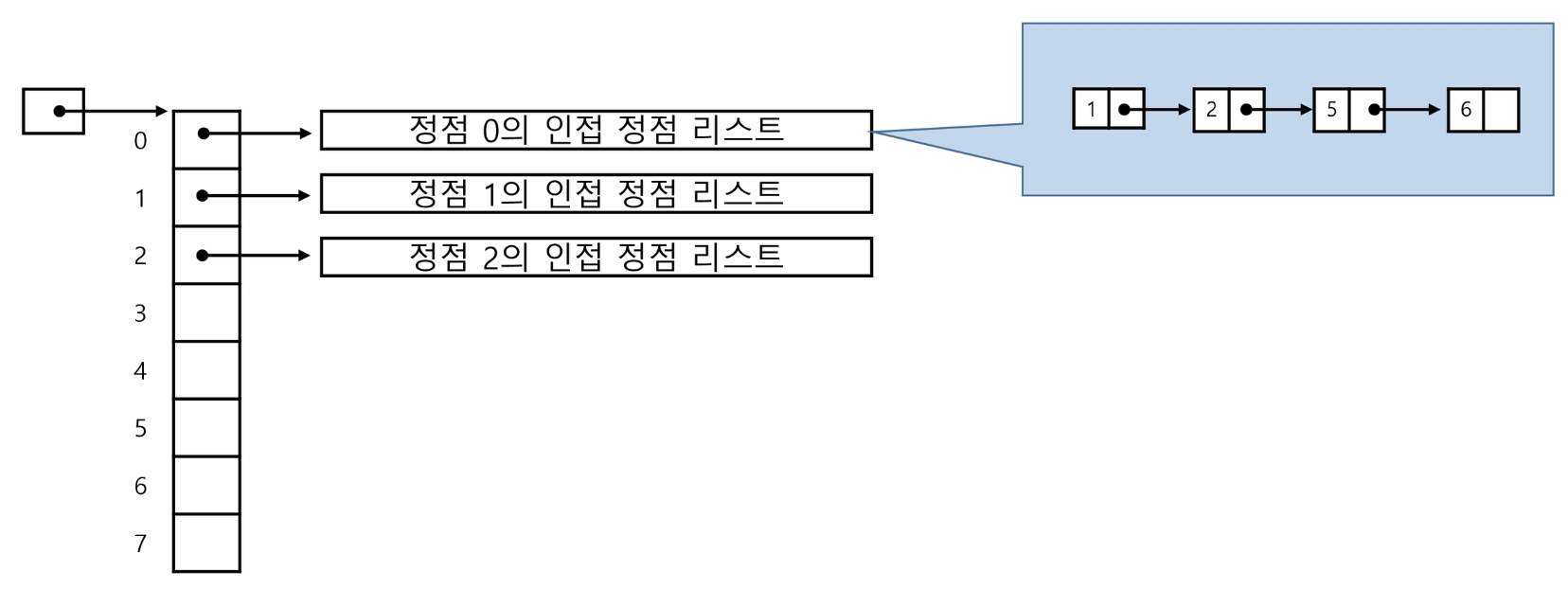
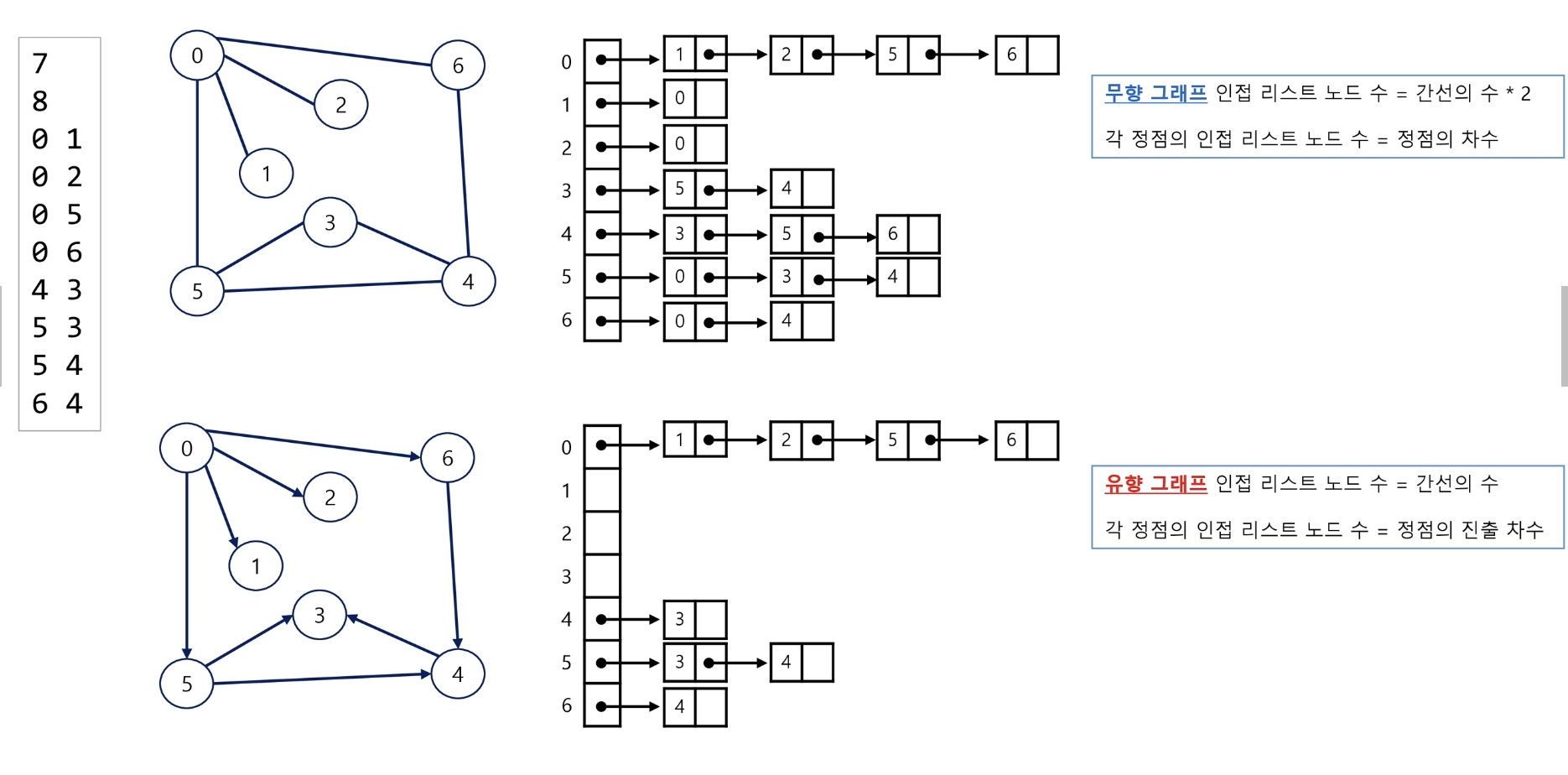
각 정점에 대한 인접 정점들을 순차적으로 표현
하나의 정점에 대한 인접 정점들을 각각 노드로 하는 연결 리스트로 저장

import java.util.ArrayList;
import java.util.Scanner;

public class AdjListTest2 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int V = sc.nextInt();       // 정점 개수
        int E = sc.nextInt();       // 간선 개수

        ArrayList<Integer>[] adjList = new ArrayList[V];   // 각 노드의 리스트
        for (int i = 0; i < V; i++) {
            adjList[i] = new ArrayList<>();
        }

        for (int i = 0; i < E; i++) {
            int from = sc.nextInt();
            int to = sc.nextInt();
            adjList[from].add(to);
            adjList[to].add(from);
        }

        for (int i = 0; i < V; i++) {
            System.out.println(adjList[i]);
        }
    }
}
/*
입력
7
8
0 1
0 2
0 5
0 6
4 3
5 3
5 4
6 4
 */
/*
출력
[1, 2, 5, 6]
[0]
[0]
[4, 5]
[3, 5, 6]
[0, 3, 4]
[0, 4]
 */