백트레킹 (Backtracking)

백트래킹(Backtracking)

• 퇴각 검색
• 모든 조합을 시도해서 문제의 해를 찾는다.
• 해를 얻을 때까지 모든 가능성을 시도한다.
• 모든 가능성은 하나의 트리처럼 구성할 수 있으며, 가지(선택지) 중에 해결책이 있다.
• 여러 가지(선택지)들이 존재하는 상황에서 하나의 가지를 선택한다.
• 선택이 이루어지면 새로운 선택지들의 집합이 생성된다.
• 이런 선택을 반복하면서 최종 상태에 도달한다.
• 보통 재귀 함수로 구현된다.

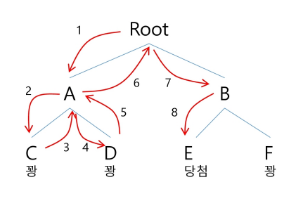
당첨 리프 노드 찾기

• 루트에서 갈 수 있는 노드를 선택한다.
• 꽝 노드까지 도달하면 최근의 선택으로 되돌아와서 다시 시작한다.
• 더 이상의 선택지가 없다면 이전의 선택지로 돌아가서 다른 선택을 한다.
• 루트까지 돌아갔을 경우 더 이상 선택지가 없다면 찾는 답이 없다.
  

8-Queens 문제

• 퀸 8개를 크기 8의 체스판 안에 서로를 공격할 수 없도록 배치하는 모든 경우를 구하는 문제
• 후보 해의 수:
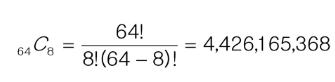
• 실제 해의 수: 이 중에서 실제 해는 92개뿐
• 즉, 44억 개가 넘는 후보 해의 수 속에서 92개를 최대한 효율적으로 찾아내는 것이 관건
• 4-Queens 문제로 축소하고 같은 행에 퀸을 두지 않는 방법으로 제한을 두어 생각해 보자
• 모든 경우의 수: 4x4x4x4 = 256
  
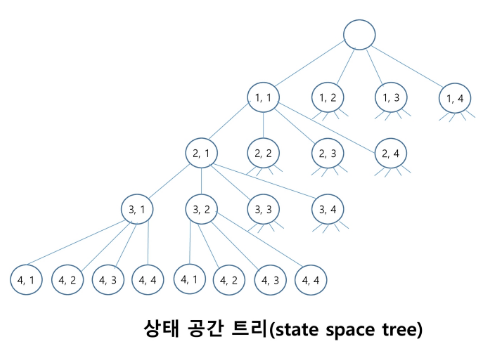
• 루트(root0) 노드에서 리프(leaf) 노드까지의 경로는 해답후보(candidate solution)가 되는데, 완전 탐색을 하여 그 해답후보 중에서 해답을 찾을 수 있다.
• 그러나 이 방법을 사용하면 해답이 될 가능성이 전혀 없는 노드의 후손 노드(descendant)들도 모두 검색해야 하므로 비효율적이다.
• 모든 후보를 검사? NO!
• 백트래킹 기법
  - 어떤 노드의 유망성을 점검한 후에 유망(promising)하지 않다고 결정되면 그 노드의 부모로 되돌아가(backtracking) 다음 자식 노드로 간다.
  • 유망(promising)하다.
    • 어떤 노드를 방문하였을 때 그 노드를 포함한 경로가 해답이 될 수 있으면 유망하다고 한다.
  • 가지치기(pruning)
    • 유망하지 않은 노드가 포함되는 경로는 더 이상 고려하지 않는다.

백트래킹을 이용한 알고리즘 절차

1. 상태 공간 트리의 깊이 우선 탐색을 실시한다.
2. 각 노드가 유망한지를 점검한다.
3. 만일 그 노드가 유망하지 않으면, 그 노드의 부모 노드로 돌아가서 다른 노드로의 검색을 계속한다.

일반 백트래킹 알고리즘

backtrack(node v)
	IF promising(v) == false then return;
    IF there is a solution at v
    	write the solution
    ELSE
    	FOR each child u of v
        	backtrack(u)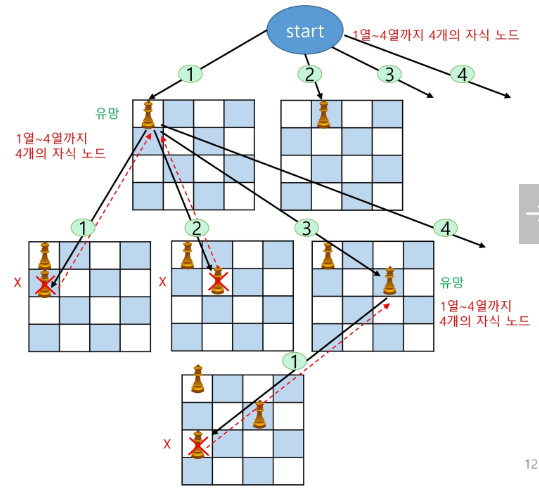

NQueen

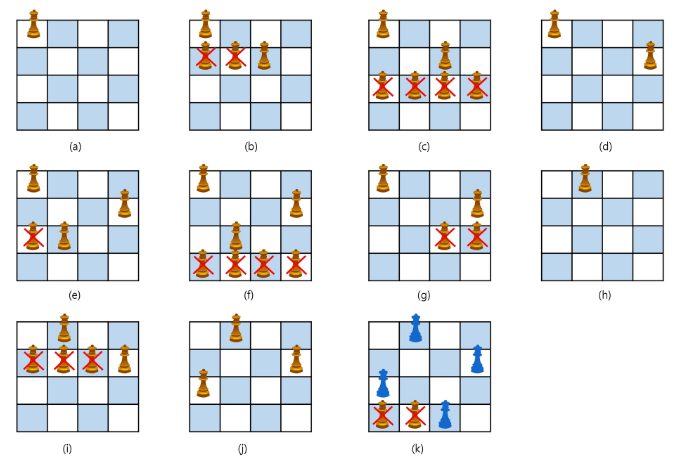
백트래킹과 완전 탐색(DFS)과의 차이

• 어떤 노드에서 출발하는 경로가 해결책으로 이어질 것 같지 않으면 더 이상 그 경로를 따라가지 않음으로써 시도의 횟수를 줄임.(Pruning 가지치기)
• 완전 탐색이 모든 경로를 추적하는데 비해 백트레킹은 불필요한 경로를 조기에 차단한다.
• 완전 탐색을 가하기에는 경우의 수가 너무나 많다.
  (예를 들어, N! 가지의 경우의 수를 가진 문제에 대해 완전 탐색을 가하면 당연히 처리 불가능한 문제)
• 백트래킹 알고리즘을 적용하면 일반적으로 경우의 수가 줄어들지만 이 역시 최악의 경우에는 여전히 지수함수 시간(Exponential Time)을 요하므로 처리 불가능할 수 있다.
• 상태 공간 트리(가능한 첫번째 해를 만날 때까지의 경우로 가정)
• 같은 행에 퀸을 두지 않는 방식의 깊이 우선 탐색 (155 노드 탐색) VS 백트래킹 (27 노드 탐색)
  
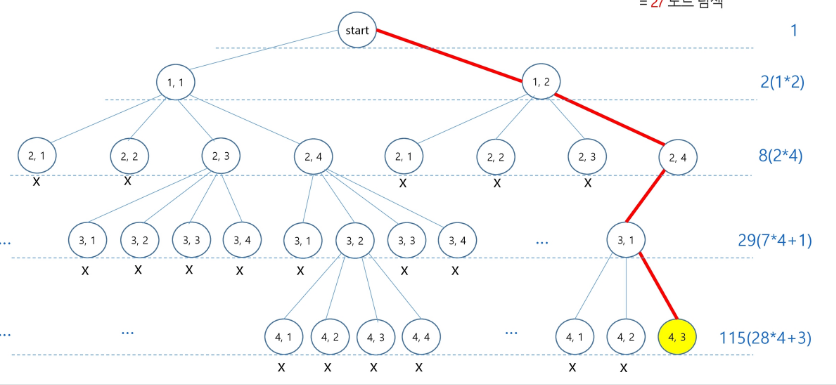
• 백트래킹은 모든 가능한 경우의 수 중에서 특정한 조건을 만족하는 경우만 살펴보는 것
• 답이 될 만한지 판단하고 그렇지 않으면 그 부분까지 탐색하는 것을 하지 않고 가지치기 하는 것
• 주로 문제 풀이에서는 DFS로 모든 경우의 수를 탐색하는 과정에서, 조건으로 답이 절대로 될 수 없는 상황을 정의하여 체크하고, 그러한 상황일 경우에는 탐색을 중지시킨 뒤 그 이전으로 돌아가서 다시 다른 경우를 탐색하게끔 구현할 수 있다.