1. 벡터

Bryant·2025년 10월 21일
0

선형대수

목록 보기
1/3

선형대수(linear algebra)의 가장 기본이 되는 개념은 벡터(vector)다.

벡터에 대해 이해하는 관점은 여러 가지가 있으며, 크게 세 가지 시각으로 나눌 수 있다.

🔹 (1) 물리학적 관점 (Physics perspective)

  • 벡터는 공간 속의 화살표(arrow in space)로 생각한다.
  • 벡터를 정의하는 두 가지 요소는:
    • 길이(length)
    • 방향(direction)
  • 화살표가 어디에 놓여 있는지는 중요하지 않다. 길이와 방향이 같다면 같은 벡터로 본다.
  • 2차원 공간에 사는 벡터는 2차원 벡터(2D vector), 우리가 사는 3차원 공간에 존재하는 벡터는 3차원 벡터(3D vector)다.

🔹 (2) 컴퓨터 과학적 관점 (Computer science perspective)

  • 벡터는 순서가 있는 숫자의 리스트(ordered list of numbers)다. 예를 들어, 집값을 분석할 때 두 가지 속성만 고려한다고 하자:
    • 집의 면적(square footage)
    • 가격(price)
  • 하나의 집을 (면적, 가격)의 쌍으로 표현할 수 있다. 즉, (x₁, x₂) 형태의 2차원 벡터로 나타낸다.
  • 여기서 순서(order)가 매우 중요하다. (100, 200)과 (200, 100)은 전혀 다른 벡터다.
  • 이 관점에서 “벡터”란 사실상 숫자 리스트(list of numbers)를 의미한다. 리스트의 길이가 벡터의 차원(dimension)을 결정한다.

🔹 (3) 수학적 관점 (Mathematical perspective)

  • 수학자는 위 두 관점을 일반화(generalize)하려 한다.
  • 즉, 벡터는 다음 두 연산이 정의될 수 있는 모든 대상을 말한다:
    • 벡터 덧셈(vector addition)
    • 스칼라 곱(scalar multiplication)
  • 이 정의는 추상적이지만, 선형대수 전반에 걸쳐 매우 중요한 기초가 된다. (이 강의에서는 먼저 구체적 관점으로 이해하고, 마지막에 추상적 정의로 돌아올 예정이다.)

2. 좌표계와 벡터의 표현

선형대수에서는 벡터의 시각적 이해가 중요하다.

우리는 벡터를 좌표계(coordinate system) 속의 화살표(arrow)로 생각한다.

이때 벡터의 꼬리(tail)는 항상 원점(origin)에 고정되어 있다.

🔸 2차원 벡터 (2D vector)

  • x축(x-axis): 수평(horizontal) 방향
  • y축(y-axis): 수직(vertical) 방향
  • 원점(origin)은 두 축이 만나는 지점이며, 모든 벡터의 기준점이다.

벡터의 좌표 (x, y)는 원점에서 벡터의 끝(tip)까지의 이동을 나타낸다.

좌표 구성요소의미
첫 번째 수 xx축을 따라 이동한 거리 (양수면 오른쪽, 음수면 왼쪽)
두 번째 수 yy축과 평행한 방향으로 이동한 거리 (양수면 위쪽, 음수면 아래쪽)

표기 방식:

v⃗=[xy]\vec{v} = \begin{bmatrix} x \\ y \end{bmatrix}

이 표기법은 점(point)과 구분하기 위한 관례다.

🔸 3차원 벡터 (3D vector)

  • 세 번째 축인 z축(z-axis)을 추가한다. 이는 x축과 y축 모두에 수직(perpendicular)이다.
  • 하나의 벡터는 세 개의 수로 표현된다:
v⃗=[xyz]\vec{v} = \begin{bmatrix} x \\ y \\ z \end{bmatrix}
  • 각 성분은 다음을 의미한다:
    • x: x축 방향으로의 이동
    • y: y축 방향으로의 이동
    • z: z축 방향으로의 이동

3. 벡터의 덧셈 (Vector addition)

벡터의 덧셈은 두 이동(movement)을 연속적으로 수행하는 것과 같다.

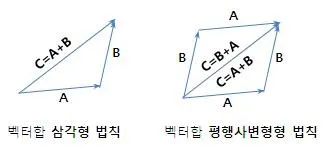
🔸 기하적 정의 (Geometric definition)

  1. 첫 번째 벡터의 끝(tip)에 두 번째 벡터의 꼬리(tail)를 붙인다.
  2. 첫 번째 벡터의 꼬리에서 두 번째 벡터의 끝까지 그은 새로운 화살표가 합벡터(sum vector)다.

이는 “tip-to-tail method”라고 부른다.

💡 직관적 의미:

첫 번째 벡터만큼 이동하고, 그 다음 두 번째 벡터만큼 이동하는 전체 효과는 두 벡터의 합과 동일하다.

🔸 수치적 정의 (Numeric definition)

예를 들어,

a⃗=[12],b⃗=[3−1]\vec{a} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}, \quad \vec{b} = \begin{bmatrix} 3 \\ -1 \end{bmatrix}

이라면,

a⃗+b⃗=[1+32+(−1)]=[41]\vec{a}+\vec{b}= \begin{bmatrix} 1 +3\\ 2 + (-1) \end{bmatrix} = \begin{bmatrix} 4\\ 1 \end{bmatrix}

즉, 각 성분(component)을 서로 더한다:

(a1,a2,...,an)+(b1,b2,...,bn)=(a1+b1,a2+b2,...,an+bn)(a_1,a_2,...,a_n) + (b_1,b_2,...,b_n) = (a_1+b_1, a_2+b_2,...,a_n+b_n)

4. 스칼라 곱 (Scalar multiplication)

🔸 정의

스칼라 곱은 벡터를 늘이거나(stretch), 줄이거나(squish), 뒤집는(flip) 연산이다.

  • 스칼라(scalar): 벡터에 곱해지는 숫자(number)
  • 스칼라가 하는 일: 벡터의 길이(scale)를 조정한다.
스칼라 값변화
2길이가 2배로 늘어남
1/3길이가 1/3로 줄어듦
-1.8방향이 반대로 뒤집히고, 길이가 1.8배로 늘어남

🔸 수치적 정의

c⋅[xy]=[c⋅xc⋅y]c \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} c \cdot x \\ c \cdot y \end{bmatrix}

즉, 스칼라 곱은 각 성분을 스칼라 값으로 곱한다.

5. 두 관점의 연결 (Connecting the two views)

  • 기하적 관점(geometric view): 벡터를 화살표로 본다.
  • 수치적 관점(numeric view): 벡터를 숫자 리스트로 본다.

선형대수의 핵심은 이 두 관점을 자유롭게 오가는 능력이다.

이는 데이터 분석가, 물리학자, 컴퓨터 그래픽스 프로그래머 모두에게 중요한 사고방식이다.

예를 들어:

  • 데이터 분석가는 숫자들의 집합을 시각적으로 해석할 수 있고,
  • 그래픽 프로그래머는 공간 상의 물체를 숫자로 표현해 연산할 수 있다.

6. 핵심 요약 (Summary)

개념설명
벡터(Vector)방향과 크기를 가진 수학적 객체
벡터의 표현2D에서는 (x, y), 3D에서는 (x, y, z)
벡터 덧셈(Vector addition)각 성분을 더하거나, 두 이동을 연속으로 수행
스칼라 곱(Scalar multiplication)벡터의 길이를 조정하거나 방향을 반전
스칼라(Scalar)벡터를 스케일링하는 숫자
핵심 관점화살표(기하적) ↔ 숫자 리스트(수치적) 간의 변환 능력
profile
Bryant
Data analysis, statistics
다음 포스트

선형결합(Linear Combinations), 스팬(Span), and 기저 벡터(Basis Vector)

0개의 댓글