선형결합(Linear Combinations), 스팬(Span), and 기저 벡터(Basis Vector)

1️⃣ 좌표와 기저 벡터 (Coordinate & Basis)

• 단위벡터(unit vector): 크기가 1인 벡터
  • $\hat{i} = (1,0)$ → 2차원 공간 기준
  • $\hat{j} = (0,1)$
• 2차원 벡터 (3,−2)는 두 개의 스칼라(3, -2)로 표현됨.
  • 3은 x축 방향 단위벡터 $\hat{i}$를 3배로 늘린 것
  • 2는 y축 방향 단위벡터 $\hat{j}$를 뒤집고 2배로 늘린 것
• 결국 (3,−2)는 $3\hat{i}+(-2)\hat{j}$ 로 나타낼 수 있다. 👉 즉, 좌표는 "각 기저 벡터를 얼마나 스케일링했는가"를 나타냄.
  

---

2️⃣ 기저 (Basis)

• 표준기저(standard basis): 단위벡터로 이루어진 집합
  • $standard~basis =(\hat{i},\hat{j}) = {(1,0),(0,1)}$
• 하지만, 임의의 두 벡터를 기저로 사용할 수도 있음.
  • 단, 그 두 벡터가 서로 다른 방향을 가질 때만 유효.
• 기저를 바꾸면, 같은 벡터라도 좌표값이 달라짐.

  → 좌표는 "기저 벡터의 선택"에 따라 달라지는 상대적인 값이다.

---

3️⃣ 선형결합 (Linear Combination)

• 벡터를 스칼라로 스케일링하고 더한 것을 말함. $a\vec{v_1} + b\vec{v_2}$
• “Linear”라는 말은, 한 스칼라만 바꿀 때 벡터의 끝점이 직선(line) 을 그리기 때문.

---

4️⃣ 스팬 (Span)

• 주어진 벡터 집합으로 만들 수 있는 모든 선형결합의 집합.
• 예시:
  • 2D 공간에서 두 벡터가 같은 선 위에 있지 않다면 → 모든 2D 벡터를 생성 가능 (즉, 평면 전체가 스팬)
  • 두 벡터가 같은 선상에 있다면 → 그 선 위의 벡터들만 생성 가능
• 요약:

  span(v1, v2) = { a*v1 + b*v2 | a, b ∈ ℝ }

---

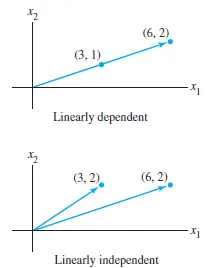
5️⃣ 선형독립 vs 선형종속 (Linear Independence / Dependence)

• 여러 벡터 중 하나가 다른 벡터들의 선형결합으로 표현될 수 있으면 → 선형종속(linearly dependent)
• 그렇지 않고, 각 벡터가 새로운 방향(차원)을 추가하면 → 선형독립(linearly independent)

예시:

• 위 세 벡터를 선형결합(각 벡터의 스칼라곱)했을 때, 각 벡터가 각자 다른 차원을 추가한다. 따라서, 위는 선형 독립(Linearly independent)

---

6️⃣ 기저의 수학적 정의

Basis = 선형독립인 벡터들이면서, 그 벡터들이 전체 공간을 스팬하는 집합

• 예:
  • 2D 공간의 표준기저 → $\{ \hat{i}, \hat{j} \}$
  • 3D 공간의 표준기저 → $\{ \hat{i}, \hat{j}, \hat{k} \}$
• 각각이 새로운 방향을 제공하고, 전체 공간의 모든 벡터를 표현할 수 있음.

---

💡 시각적 직관 요약

상황	결과 (Span)	비고
1개의 2D 벡터	선(Line)	1차원
2개의 2D 벡터 (같은 방향)	선(Line)	1차원 (종속)
2개의 2D 벡터 (다른 방향)	평면(Plane)	2차원 (독립)
3개의 3D 벡터 (모두 독립)	공간(Space)	3차원

---