Linear Transformation & Matrices

Bryant·2025년 10월 27일
0

선형대수

목록 보기
3/3

1. 선형변환(Linear Transformation)이란?

🔹 개념

  • 변환(Transformation): 입력으로 벡터를 받아 다른 벡터를 출력하는 함수(function).
T(v⃗)=w⃗T(\vec{v}) = \vec{w}

의 형태로, 벡터 v를 벡터 w로 이동시키는(Transform) 함수다.

🔹 시각적 이해 (Geometric Interpretation)

벡터를 “화살표”가 아닌 “화살표의 끝점(point)”으로 보면, 변환이란 공간상의 모든 점이 새로운 위치로 이동하는 과정으로 볼 수 있다.

  • 모든 벡터(=점)가 새로운 좌표로 이동한다.
  • 변환 전체를 보면, 공간이 움직이거나 찌그러지는(squishing/morphing) 듯한 효과가 생긴다.

2. 선형변환(Linear Transformation)의 조건

선형대수에서는 아무 변환이나 다루지 않는다. 특정한 두 가지 성질을 만족해야 선형(linear)이라고 부른다.

조건설명
① 직선 보존(Line preservation)직선(line)은 곡선(curve)으로 변하지 않는다.
② 원점 보존(Origin fixed)원점(origin)은 이동하지 않는다.

즉, 격자(grid)를 변형하더라도 격자선이 평행(parallel)하고 균일하게 간격이 유지(evenly spaced)되어야 한다.

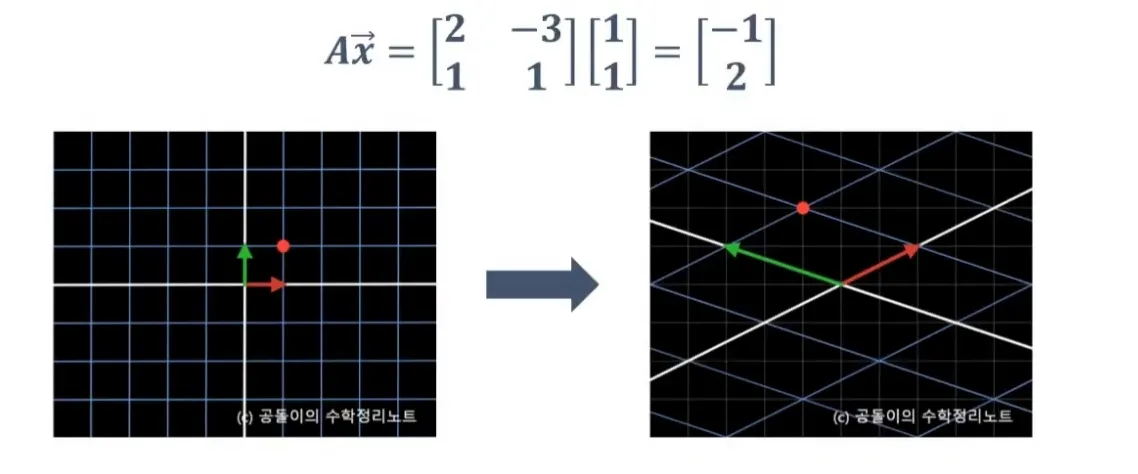
3. 변환을 숫자로 표현하기

🔹 기본 벡터(Basis vectors)

2차원 공간에서 모든 벡터는 두 개의 기저벡터(basis vectors)

i^=[10],j^=[01]\hat{i} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \quad \hat{j} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}

의 선형결합(linear combination)으로 표현된다.

예:

v⃗=−1i^+2j^\vec{v}=-1\hat{i}+2\hat{j}

🔹 핵심 아이디어

선형변환에서는 i-hat과 j-hat이 각각 어디로 가는지만 알면,

모든 벡터의 이동 결과를 예측할 수 있다.

즉,

T(v⃗)=−1∗T(i^)+2∗T(j^)T(\vec{v}) = -1*T(\hat{i}) + 2 *T(\hat{j})

4. 예시

예시 1️⃣

변환 후:

i^→(1,−2)j^→(3,0)\hat{i} → (1, -2) \\ \hat{j} → (3, 0)

그렇다면,

v⃗=−1i^+2j^\vec{v} = -1\hat{i} +2\hat{j}

은 다음으로 이동한다:

T(v⃗)=−1(1,2)+2(3,0)=(5,2)T(\vec{v}) = -1(1,2) +2(3,0) = (5,2)

이제 변환 전체를 보지 않아도, i^,j^\hat{i}, \hat{j}의 이동만으로 모든 벡터의 결과를 구할 수 있다!

5. 행렬(Matrix)과의 관계

이제 행렬(matrix)은 선형변환을 기록하는 방식으로 이해할 수 있다.

🔹 행렬의 구성

2D 변환의 경우,

Matrix=[abcd]\text{Matrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}
  • 첫 번째 열(column): i^\hat{i}가 이동한 좌표
  • 두 번째 열(column): j^\hat{j}가 이동한 좌표

즉,

[abcd]=[T(i^)    T(j^)]\begin{bmatrix} a & b \\ c & d \end{bmatrix} = \left[ T(\hat{i}) \;\; T(\hat{j}) \right]

🔹 행렬-벡터 곱(Matrix-Vector Multiplication)

[abcd][xy][ax+bycx+dy]\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix}

이는 곧,

xT(i^)+yT(j^)xT(\hat{i}) + yT(\hat{j})

와 같다.

즉, 벡터를 스케일링(scaling)하고 더하는 연산 = 선형변환의 계산 방식이다.

6. 대표적인 선형변환 예시

image.png

7. 선형종속(Linear Dependence)과 공간의 압축

T(i)T(i^)T(T(i^)T(\hat{i})T(

만약 T(i^)와T)j^)T(\hat{i})와 T)\hat{j})가 선형종속(linearly dependent)이라면 (즉, 하나가 다른 하나의 스칼라배라면) 모든 2차원 공간이 한 직선(line) 위로 눌려버린다. 이걸 “2차원 → 1차원으로 압축(squish)”한다고 표현한다.

8. 요약 (Summary)

개념설명
선형변환(Linear Transformation)공간을 움직이는 함수로, 직선 유지 & 원점 고정
기저벡터(Basis vectors)공간의 방향을 정의하는 기본 벡터들
행렬(Matrix)각 기저벡터가 이동한 좌표를 열(column)로 기록한 것
행렬-벡터 곱(Matrix-vector multiplication)선형변환을 수치적으로 계산하는 방법
선형종속(Linear dependence)한 벡터가 다른 벡터의 배수일 때. 공간이 압축됨
profile
Bryant
Data analysis, statistics
이전 포스트

선형결합(Linear Combinations), 스팬(Span), and 기저 벡터(Basis Vector)

0개의 댓글