삼각비
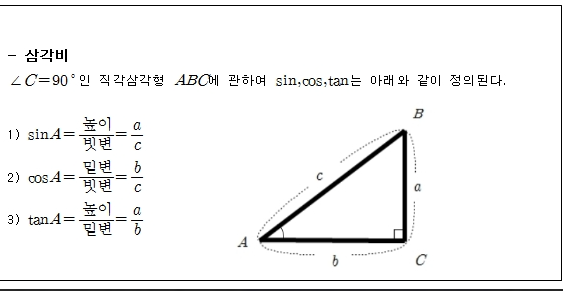
삼각비는 직각삼각형에서 각 변의 비율을 나타낸 것이다.
sinθ=빗변높이
cosθ=높이밑변
tanθ=밑변높이
단위원으로 확장하기
90도가 넘어가면 삼각형을 그리지 못하는데, 이 때 단위원 (반지름 1인 원)을 사용해 모든 각도에서 삼각함수를 정의할 수 있다.
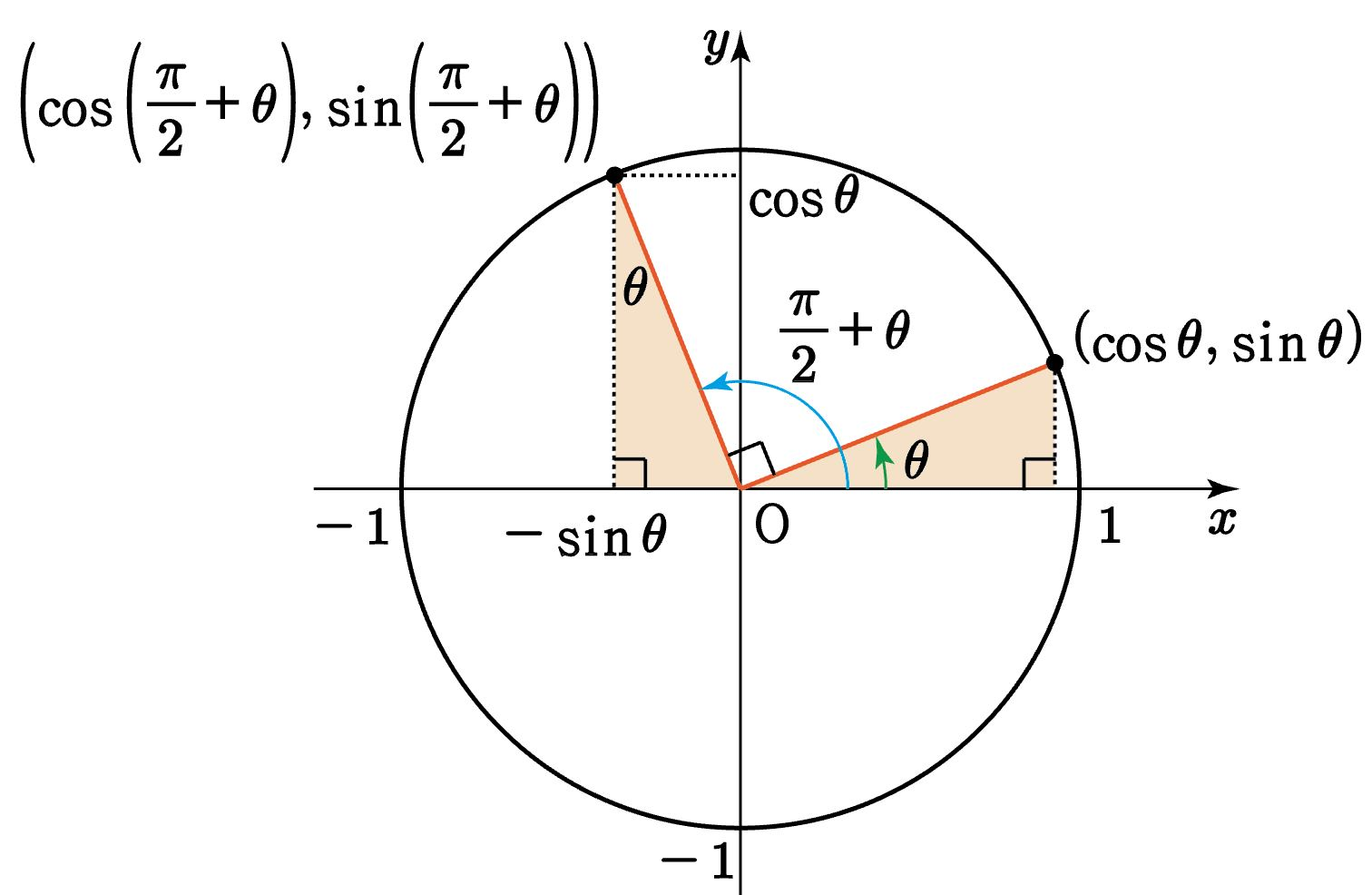
sinθ=ry
cosθ=rx
tanθ=xy
삼각함수의 제곱공식
sin2x+cos2x=1
증명
P(X,Y)에서 x2+y2=r2의 양변을나누면(rx)2+(ry)2=1rx=sinx, ry=cosx
주기함수
각도 theata를 일반적인 f(x) = y 형태로 표시하면 주기성을 지니는 주기함수가 된다.
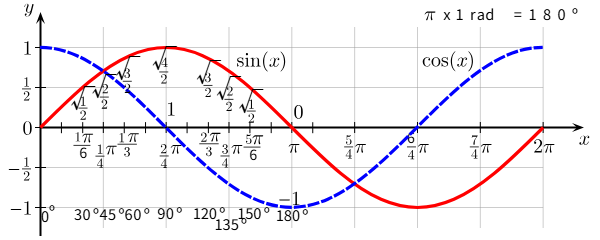
sinx=sin(x+2nπ)cosx=cos(x+2nπ)
위가 성립하므로 sin함수와 cos 함수는 주기가 2pi인 주기함수이다.
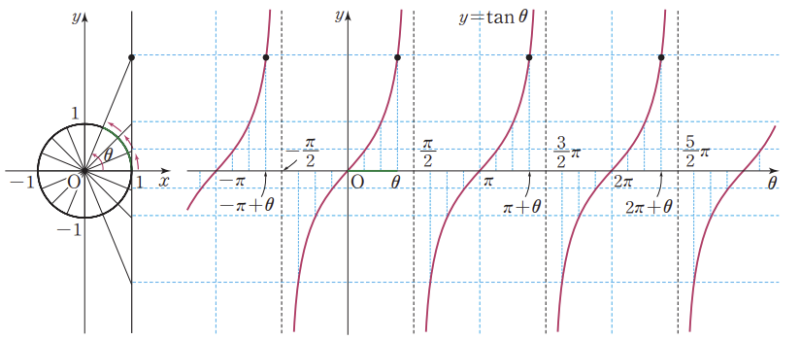
tan 함수는 pi의 주기를 가지는 주기함수이다.
주기함수는 다음과 같은 성질을 가진다.
sin(−x)=−sinx, cos(−x)=cosxsin(x+2π)=cosx, cos(x+2π)=−cosxsin(x+π)=−sinx, cos(x+π)=−cosx
일반적인 주기함수에서 주기는 2pi/w, 주파수는 w, 진폭은 |A|, 위상각은 phi
y=Asin(ws+ϕ) 



