문제 풀이
1. 백준 2206 - 벽 부수고 이동하기
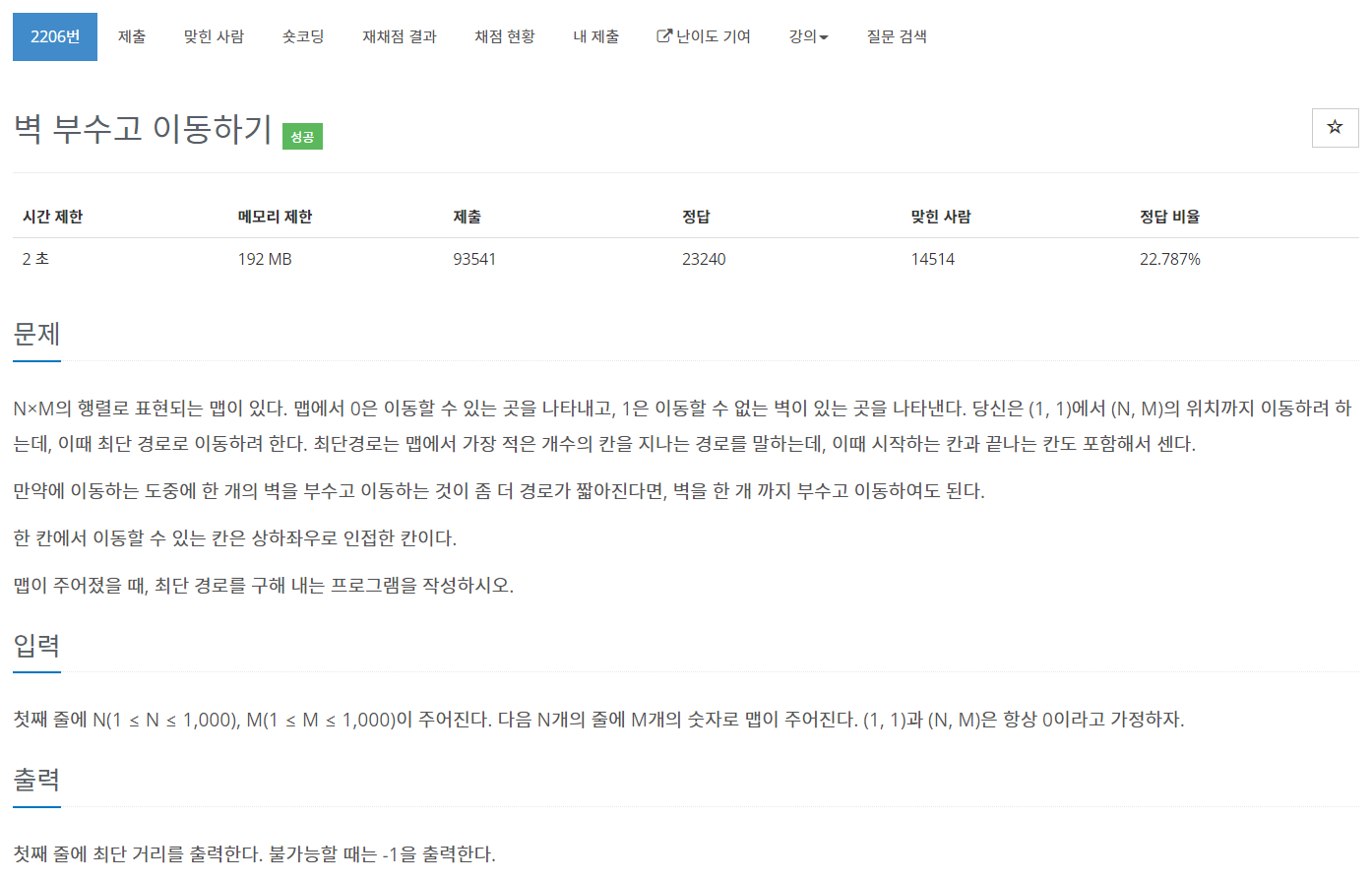
정말 간단해 보이지만 그래도 탐색 문제의 응용된 형태라는 느낌이 드는 문제였다. 기존의 최소경로 탐색 문제에서 달라진 점은, 지나가지 못하던 벽에 대한 조건이 하나 추가된 것이다.
처음 접근했던 방법은 노드 클래스에 벽을 부쉈는 지 여부를 저장하는 멤버 하나를 추가하는 방법이었다. 기존과 똑같이 구현하지만 벽을 최대 한 번 부수도록 제한만 한 것이다. 하지만 이렇게 했을 때 생기는 문제가 있었다. 이미 벽을 넘어간 노드가 이동한 좌표에는 벽을 넘어간 적 없는 노드들도 갈 수 없게 되는 것이다.
예를 들어서 벽을 넘어 지나간 노드가 다른 노드들보다 먼저 이동해 뒷쪽의 노드들을 모두 visited로 바꿔버리고나서 벽을 마주쳐 탐색을 끝내버렸다. 뒤늦게 온 벽을 부순 적 없는 노드들은 visited가 되어버린 좌표들을 밟지 못하고 탐색이 종료되어버린다. 다시 말해, 이 경우엔 탐색의 경우의 수를 모두 afford하지 못한다. 따라서 벽을 넘은 경우와 벽을 넘지 않은 경우의 visited를 따로 정의할 필요가 있다.
그래서 나는 visited를 3차원 배열로 선언했다.
package BFS;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
public class BOJ2206 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] a = br.readLine().split(" ");
int n = Integer.parseInt(a[0]);
int m = Integer.parseInt(a[1]);
if (n == 1 && m == 1) {
System.out.println(1);
return;
}
int[] dx = {1, 0, -1, 0};
int[] dy = {0, 1, 0, -1};
int[][] board = new int[n][m];
int[][][] visited = new int[2][n][m];//visited[0]이 안깼을때, [1]이 이미 깼을 때
for (int i = 0; i < 2; i++) {
for (int j = 0; j < n; j++) {
Arrays.fill(visited[i][j], -1);
}
}
Queue<Pair4> queue = new LinkedList<>();
for (int i = 0; i < n; i++) {
String[] b = br.readLine().split("");
for (int j = 0; j < m; j++) {
board[i][j] = Integer.parseInt(b[j]);
}
}
queue.offer(new Pair4(0, 0));
visited[0][0][0] = 1;
while (!queue.isEmpty()) {
Pair4 tmp = queue.poll();
int brokenVar = tmp.getBroken() ? 1 : 0;
for (int i = 0; i < 4; i++) {
int nx = tmp.getX() + dx[i];
int ny = tmp.getY() + dy[i];
if (nx == n-1 && ny == m-1) {
System.out.println(visited[brokenVar][tmp.getX()][tmp.getY()] + 1);
return;
}
if (nx < 0 || nx > n-1 || ny < 0 || ny > m-1 || visited[brokenVar][nx][ny] != -1) continue;
if (board[nx][ny] == 1) {
if (tmp.getBroken()) continue;
queue.offer(new Pair4(nx, ny, true));
visited[1][nx][ny] = visited[brokenVar][tmp.getX()][tmp.getY()] + 1;
continue;
}
queue.offer(new Pair4(nx, ny, tmp.getBroken()));
visited[brokenVar][nx][ny] = visited[brokenVar][tmp.getX()][tmp.getY()] + 1;
}
}
System.out.println(-1);
}
private static void showvisited(int[][] visited) {
System.out.println("--------visited-------");
for (int i = 0; i < visited.length; i++) {
System.out.println(Arrays.toString(visited[i]));
}
}
}Pair4는 좌표에 더해 broken이라는 boolean 변수를 갖고 있는 클래스다.
2. 백준 2573 - 빙산
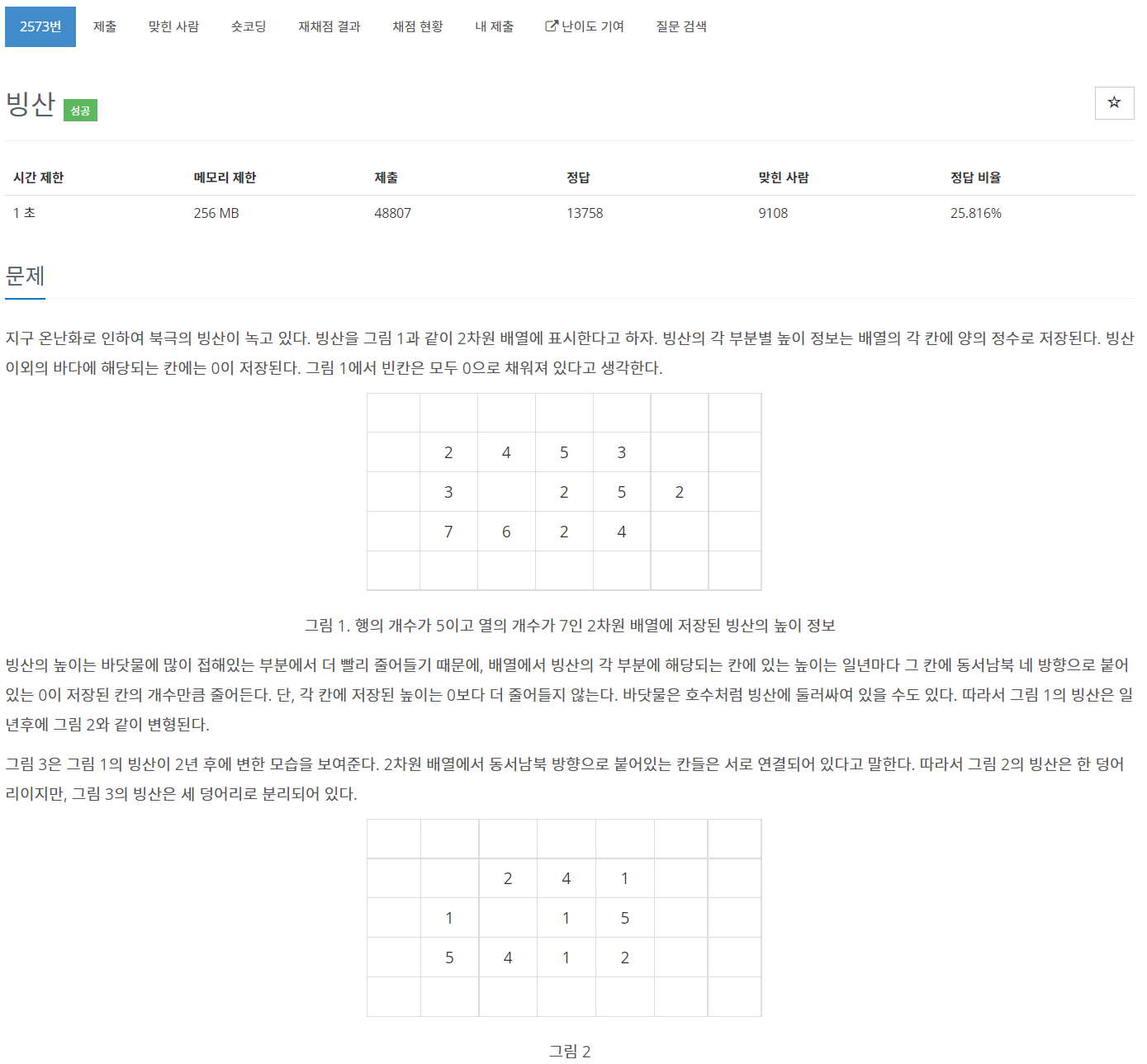
빙산을 녹이는 과정과 땅의 개수를 세는 과정 모두 땅(0이 아닌 부분)을 탐색하는 bfs를 통해 구현할 수 있다. 땅을 녹여 board에 반영한 뒤, 땅의 개수를 세서 나뉘였는지를 파악한다. 이 과정을 반복한다.
빙산의 높이가 최대 10이기 때문에 열 번의 반복 후에도 나오지 않는다면 0을 출력한다.
package BFS;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
//녹이기, bfs로 덩어리 갯수 세기 반복
public class BOJ2573 {
static int n;
static int m;
static int[][] board;
static int[] dx = {1, 0, -1, 0};
static int[] dy = {0, 1, 0, -1};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int years = 0;
String[] a = br.readLine().split(" ");
n = Integer.parseInt(a[0]);
m = Integer.parseInt(a[1]);
board = new int[n][m];
for (int i = 0; i < n; i++) {
String[] b = br.readLine().split(" ");
for (int j = 0; j < m; j++) {
board[i][j] = Integer.parseInt(b[j]);
}
}
while (true) {
melt();
showBoard();
int icebergs = bfs();
years++;
if (icebergs == 0) {
System.out.println(0);
return;
} else if (icebergs >= 2) {
System.out.println(years);
return;
}
}
}
private static int bfs() {
int result = 0;
Queue<Pair> queue = new LinkedList<>();
boolean[][] visited = new boolean[n][m];
for (int i = 1; i < n - 1; i++) {
for (int j = 1; j < m - 1; j++) {
if (board[i][j] <= 0 || visited[i][j]) {
continue;
}
queue.offer(new Pair(i, j));
while (!queue.isEmpty()) {
Pair tmp = queue.poll();
for (int k = 0; k < 4; k++) {
int nx = tmp.getX() + dx[k];
int ny = tmp.getY() + dy[k];
if (nx < 1 || ny < 1 || nx > n - 2 || ny > m - 2) continue;
if (visited[nx][ny] || board[nx][ny] <= 0) continue;
queue.offer(new Pair(nx, ny));
visited[nx][ny] = true;
}
}
result++;
}
}
return result;
}
private static void melt() {
int[][] newThang = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] > 0) {
int cnt = 0;
for (int k = 0; k < 4; k++) {
int nx = i + dx[k];
int ny = j + dy[k];
if (nx < 0 || nx > n - 1 || ny < 0 || ny > m - 1 || board[nx][ny] > 0) continue;
cnt++;
}
newThang[i][j] = board[i][j] - cnt;
}
else newThang[i][j] = 0;
}
}
board = newThang;
}
private static void showBoard() {
for (int i = 0; i < n; i++) {
System.out.println(Arrays.toString(board[i]));
}
System.out.println("------------------");
}
}
이 문제에서 내가 간과했던 점은 melt() 메서드 구현에서 발견했다. 모든 노드들의 수를 줄이는 계산을 탐색 중에 바로 반영했는데, 이렇게 되면 다른 노드 주변의 0의 개수가 영향받을 수 있다. 그래서 newThang이라는 2차원 배열에만 저장한 뒤 탐색이 끝나고 나서야 변수 board에 저장해줬다.
3. 백준 2146 - 다리 만들기
우선 BFS로 섬의 개수와 가장자리의 인덱스를 얻는 것은 필요한 과정인 것 같았는데, 다리를 구하는 방법에서 시간복잡도가 많이 잡아먹을 것 같아 고민이 많았다.
- 모든 가장자리들로부터 다른 섬까지로의 BFS로 최솟값 구하기
- 가장자리의 위치를 섬 별로 따로 저장해 서로에 대해 모두 비교해 최솟값 구하기
첫 번째 방법은 대충 생각해봤을 때 모든 가장자리에 대해서 BFS를 돌려야 하므로 최대 O(N^4)까지 나올 것 같아 우선 건너뛰었다. 물론 후자도 모든 가장자리에 대해서 비교해야하기 때문에 별반 차이가 없을 것 같았다. 그런데 어쨌든 간에 N이 100이어서 별로 상관 없을 것 같아 우선 두 번째 방법으로 풀었다.
package BFS;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class BOJ2146 {
static int[][] board;
static int n;
static int[] dx = {1, 0, -1, 0};
static int[] dy = {0, 1, 0, -1};
static boolean[][] visited;
static List<List> list;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
board = new int[n][n];
visited = new boolean[n][n];
for (int i = 0; i < n; i++) {
String[] a = br.readLine().split(" ");
for (int j = 0; j < n; j++) {
board[i][j] = Integer.parseInt(a[j]);
}
}
bfs();
for (List x : list) {
System.out.println(x);
}
int minDistance = Integer.MAX_VALUE;
for (int i = 0; i < list.size()-1; i++) {
List<Pair> list1 = list.get(i);
for (int j = i+1; j < list.size(); j++) {
List<Pair> list2 = list.get(j);
for (Pair pair1 : list1) {
for (Pair pair2 : list2) {
int distance = Math.abs(pair1.getX() - pair2.getX()) + Math.abs(pair1.getY() - pair2.getY()) - 1;
if (distance < minDistance) minDistance = distance;
}
}
}
}
System.out.println(minDistance);
}
private static void bfs() {
list = new ArrayList<>();
Queue<Pair> queue = new LinkedList<>();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 0 || visited[i][j]) continue;
queue.offer(new Pair(i, j));
visited[i][j] = true;
List<Pair> tmpList = new ArrayList<>();
while (!queue.isEmpty()){
Pair tmp = queue.poll();
boolean appended = false;
for (int k = 0; k < 4; k++) {
int nx = tmp.getX() + dx[k];
int ny = tmp.getY() + dy[k];
if (nx < 0 || ny < 0 || nx > n-1 || ny > n-1 || visited[nx][ny]) continue;
if (board[nx][ny] == 0) {
if (appended) continue;
appended = true;
tmpList.add(tmp);
continue;
}
queue.offer(new Pair(nx, ny));
visited[nx][ny] = true;
}
}
list.add(tmpList);
}
}
}
}
List<List>를 선언해서 섬마다 가장자리의 index를 저장했다. 그리고서 모든 섬에 대해서 모든 가장자리들을 비교해 최솟값을 구했다. 놀랍게도 시간초과는 뜨지 않았다.
4. 백준 13549 - 숨바꼭질 2
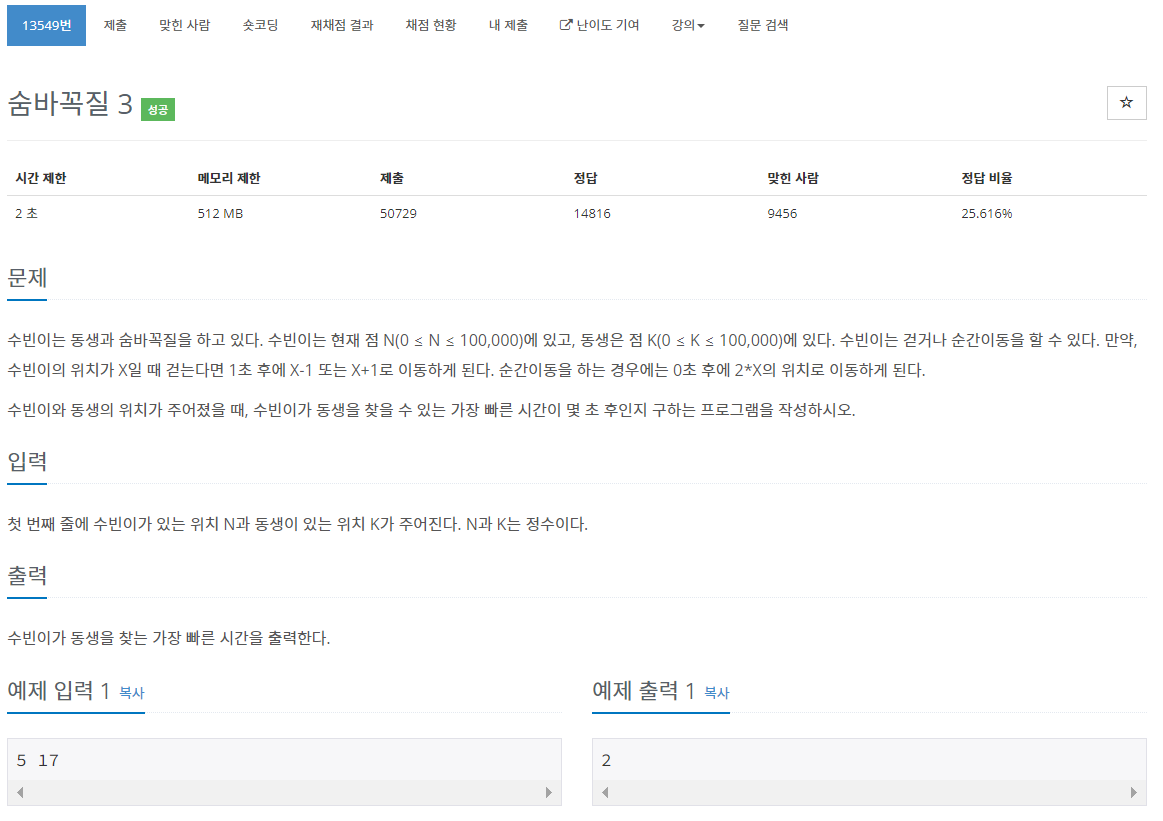지난 포스팅에서 기본 문제였던 숨바꼭질의 응용 문제다. 2*X 이동의 이동 시간을 없애 계층을 이용하는 데 제한을 줬다. 그래서 나는 수빈이의 위치를 저장하는 객체에 이동 횟수를 저장하는 멤버를 추가해 순간이동을 하는 경우를 따로 관리할 수 있도록 했다.
이동 횟수가 많지만 계층이 높아은 최솟값이 배제되는 경우 (예를 들어, 2*x 이동을 많이 사용해서, 시간 상에서는 유리하지만 bfs에서의 계층은 낮아 더욱 비효율적으로 동생을 찾는 경우가 채택되는 경우)는 고려하지 않아도 된다. 왜냐하면 당연하게도 모든 경우에서 2*x 이동을 사용하는 경우가 계층이 더 낮을 것이기 때문이다. (혹은 같은 계층이거나)
package BFS;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
class Subin {
int location;
int seconds;
public Subin(int location, int seconds) {
this.location = location;
this.seconds = seconds;
}
}
public class BOJ13549 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] a = br.readLine().split(" ");
int n = Integer.parseInt(a[0]);
int k = Integer.parseInt(a[1]);
if (n == k) {
System.out.println(0);
return;
}
boolean[] visited = new boolean[100001];
Queue<Subin> queue = new LinkedList<>();
queue.offer(new Subin(n, 0));
visited[n] = true;
while (!queue.isEmpty()) {
Subin tmp = queue.poll();
System.out.println(queue.size());
if (tmp.location*2 <= 100000 && !visited[tmp.location*2]){
if (tmp.location*2 == k) {
System.out.println(tmp.seconds);
return;
} else {
queue.offer(new Subin(tmp.location * 2, tmp.seconds));
visited[tmp.location * 2] = true;
}
}
if (tmp.location-1 >= 0 && !visited[tmp.location-1]) {
if (tmp.location-1 == k) {
System.out.println(tmp.seconds+1);
return;
} else {
queue.offer(new Subin(tmp.location - 1, tmp.seconds + 1));
visited[tmp.location - 1] = true;
}
}
if (tmp.location + 1 <= 100000 && !visited[tmp.location + 1]) {
if (tmp.location + 1 == k) {
System.out.println(tmp.seconds + 1);
return;
} else {
queue.offer(new Subin(tmp.location + 1, tmp.seconds + 1));
visited[tmp.location + 1] = true;
}
}
}
}
}
주의할 점은, 위에서 말했듯이 x*2 이동이 동생을 찾는데 더 빠르지만, x+1, x-1 이동이 동생을 찾는 시간과 같은 계층에 있는 경우가 있다. 이 경우를 대비해서, 이 세 개 중에 2*x 이동을 가장 먼저 검사해주어야한다.
나는 시작부터 찾는 경우 (n==k)를 예외처리를 안해서 한 시간을 헤맸다. 동생을 찾지 못하는 경우는 없으므로 while문을 true로 설정해놔서, 백준 채점에서는 '틀렸습니다.'가 아니라 런타임 오류로 떠서, 원인을 찾겠답시고 이상한 짓만 한 시간 동안 했다... 극단적인 케이스 예외 처리의 중요성을 다시 느끼게 해준 문제였다.
5. 백준 1600 - 말이 되고픈 원숭이
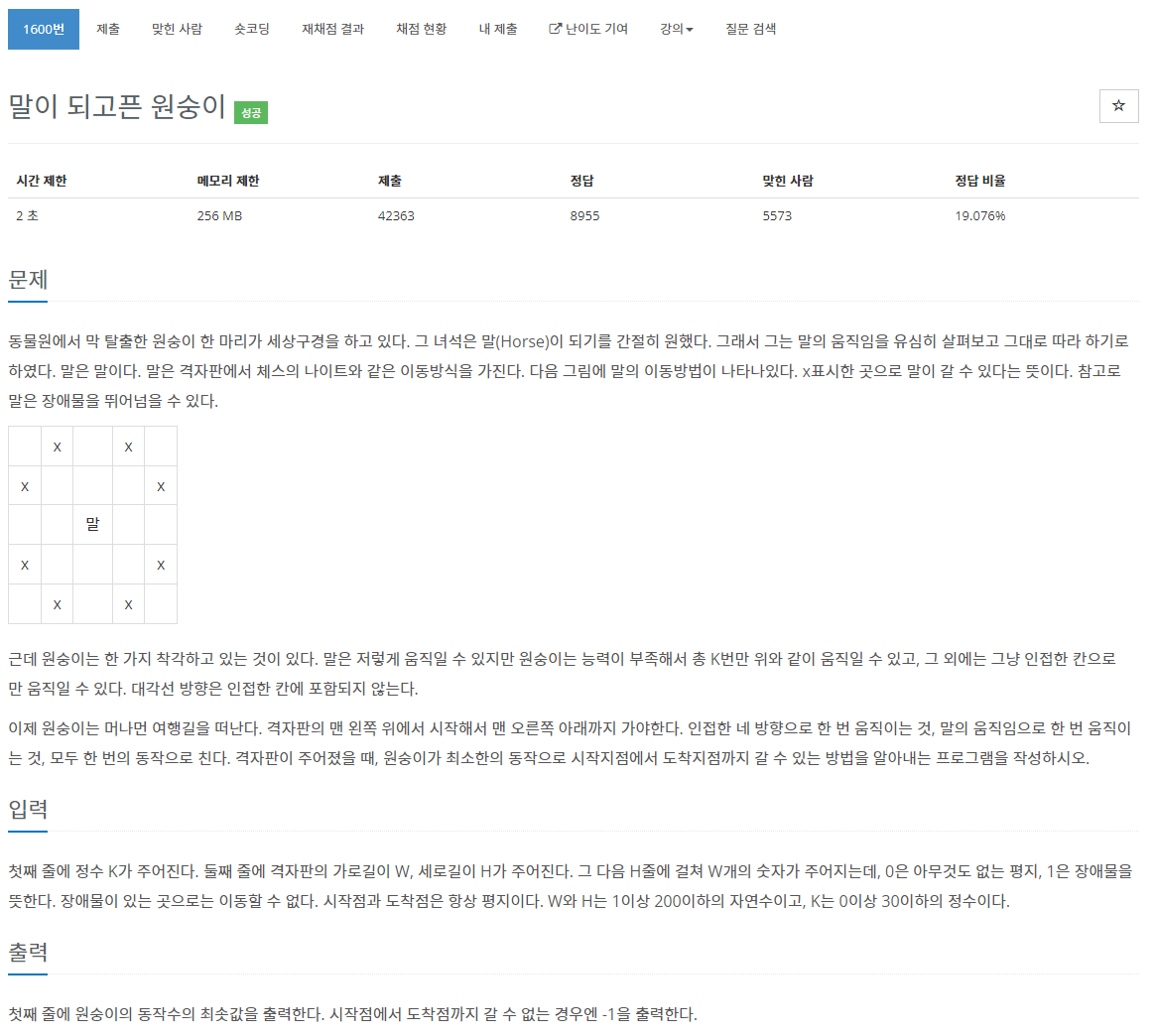말숭이 문제였다. 이전 포스팅의 나이트의 이동 문제의 응용 문제다. 지금껏 많이 써먹은 방법처럼, 점프를 한 횟수를 저장하는 멤버를 따로 만들어서 관리하면 되는 것이었다. 또 이 포스팅의 첫 번째 문제였던 벽 부수기 문제에서와 같이 점프 횟수를 기준으로 visited 변수를 다르게 가져가야 한다. 하지만 이 문제에서 점프 횟수는 boolean이 아니라 int기 때문에, 더 효율적인 방법 (해당 노드를 지나간 점프 횟수보다 더 적게 점프하고 지나갈 수 있는 경우)만을 골라서 queue에 넣어야할 것이다. 더 낮은 계층인데다가 점프까지 더 많이 한 놈은 아무 쓸모가 없다.
package BFS;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
/*
* 벽부수기 문제랑 비슷한 풀이
* visited를 int[][]로, 값은 말짬뿌를 이용한 횟수
* -> 검사하는 위치의 말짬뿌횟수가 자신의 말짬뿌횟수보다 크면 갈 수 있음. 더 효율적인 방법이라는거니께
* */
class Monkey {
int[] position;
int jumpNum;
public Monkey(int x, int y, int jumpNum) {
this.position = new int[]{x, y};
this.jumpNum = jumpNum;
}
@Override
public String toString() {
return "Monkey : [position : " + Arrays.toString(position) + ", jumpNum : " + jumpNum + "]";
}
}
public class BOJ1600 {
static int[][] board;
static int[][] visited;
static Queue<Monkey> queue;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int k = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine());
int m = Integer.parseInt(st.nextToken());
int n = Integer.parseInt(st.nextToken());
if (n == 1 && m == 1) {
System.out.println(0);
return;
}
board = new int[n][m];
visited = new int[n][m];
queue = new LinkedList<>();
int cnt = 0;
int[] dx = {1, 0, -1, 0};
int[] dy = {0, 1, 0, -1};
int[] dx2 = {-1, -2, -2, -1, 1, 2, 2, 1};
int[] dy2 = {-2, -1, 1, 2, 2, 1, -1, -2};
for (int i = 0; i < n; i++) {
Arrays.fill(visited[i], k+1);
}
for (int i = 0; i < n; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < m; j++) {
board[i][j] = Integer.parseInt(st.nextToken());
}
}
queue.offer(new Monkey(0, 0, 0));
visited[0][0] = 0;
while (!queue.isEmpty()) {
int tmpSize = queue.size();
System.out.println(queue);
cnt++;
for (int i = 0; i < tmpSize; i++) {
Monkey tmpMonkey = queue.poll();
for (int j = 0; j < 4; j++) {
int nx = tmpMonkey.position[0] + dx[j];
int ny = tmpMonkey.position[1] + dy[j];
if (nx == n-1 && ny == m-1) {
System.out.println(cnt);
return;
}
if (nx < 0 || ny < 0 || nx > n-1 || ny > m-1) continue;
if (visited[nx][ny] <= tmpMonkey.jumpNum || board[nx][ny] == 1) continue;
queue.offer(new Monkey(nx, ny, tmpMonkey.jumpNum));
visited[nx][ny] = tmpMonkey.jumpNum;
}
if (tmpMonkey.jumpNum < k) {
for (int j = 0; j < 8; j++) {
int nx = tmpMonkey.position[0] + dx2[j];
int ny = tmpMonkey.position[1] + dy2[j];
if (nx == n-1 && ny == m-1) {
System.out.println(cnt);
return;
}
if (nx < 0 || ny < 0 || nx > n-1 || ny > m-1) continue;
if (visited[nx][ny] <= tmpMonkey.jumpNum+1 || board[nx][ny] == 1) continue;
queue.offer(new Monkey(nx, ny, tmpMonkey.jumpNum+1));
visited[nx][ny] = tmpMonkey.jumpNum+1;
}
}
}
}
if (queue.isEmpty()) System.out.println(-1);
}
}
위에서 설명했듯이, 점프를 이용한 이동은 jumpNum을 늘려주고, 이미 지나간 적이 있는 위치라도 점프 횟수를 비교해 판단했다.
BFS 마무리
드디어 BFS 관련 연습문제들을 모두 해결했다. 약 열 다섯 문제 정도 됐던 것 같다. 다른 단원에 비해서 세 배는 시간이 걸렸다. 하지만 연습문제가 많다는 것은 그만큼 많이 쓰이는 알고리즘이라고 생각하고 쓰이는 경우를 나름대로 일반화하고 구현을 체화하려고 노력했다.
연습문제 출처 : encrypted-def github
컴퓨터 사이언스, 알고리즘, 모든 애플리케이션에 관심이 있습니다.