What is Decision Trees?

Decision Tree는 Regression과 Classification에 사용 가능한 Supervised Model이다.

Decision Tree Components

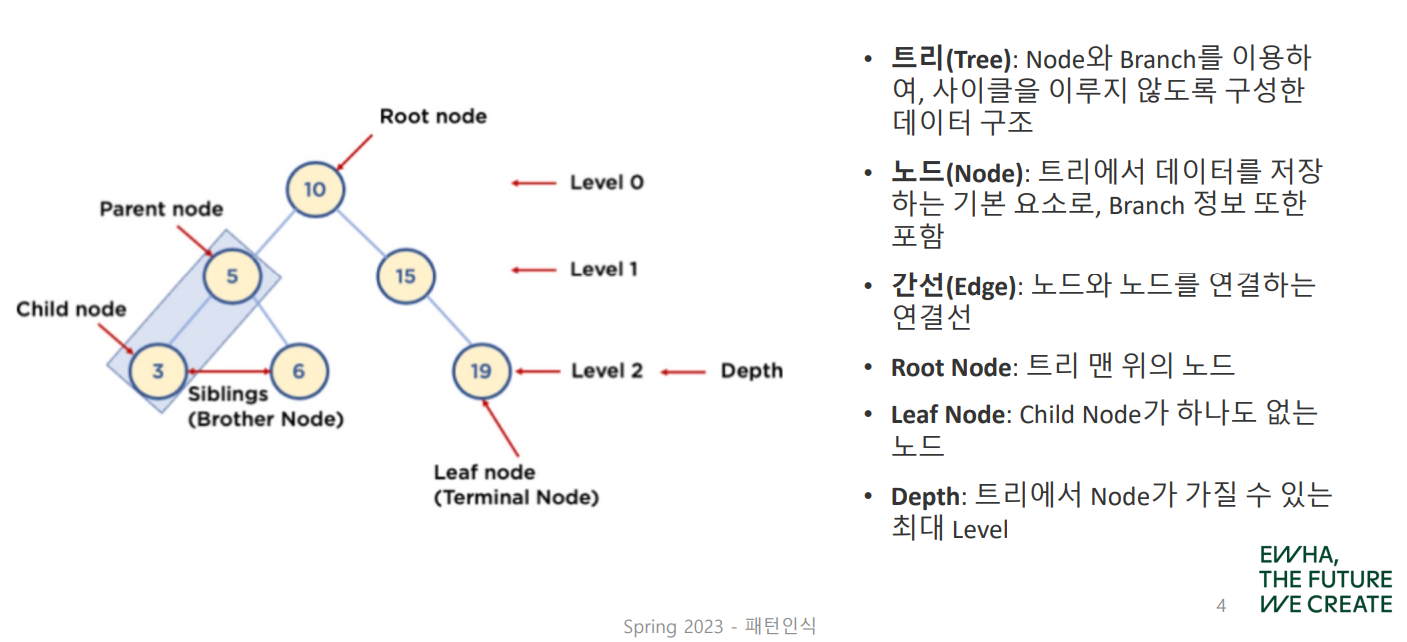
• Root node: 맨 처음 분류기준 (딱 1개뿐이다!)
• Intermediate node: 중간 분류기준
• Leaf node: 맨 마지막 분류기준

Decision Tree 모델의 궁극적인 목표는
Leaf node의 복잡성(불순도)을 최소화하는 것!
참고로 자식노드의 불순도는 반드시 부모노드보다 작아야 하며, 이를 자식이 정보를 획득(Information Gain)했다고 말한다.

Decision Trees for Classification

Root node와 Intermediate node는 feature, Leaf node는 결괏값, 즉 Decision Tree는 hypothesis function이라고 볼 수 있다.

Decision Tree를 이용해서 다음 표를 보고 테니스하기 좋은 날을 분류해 보자!

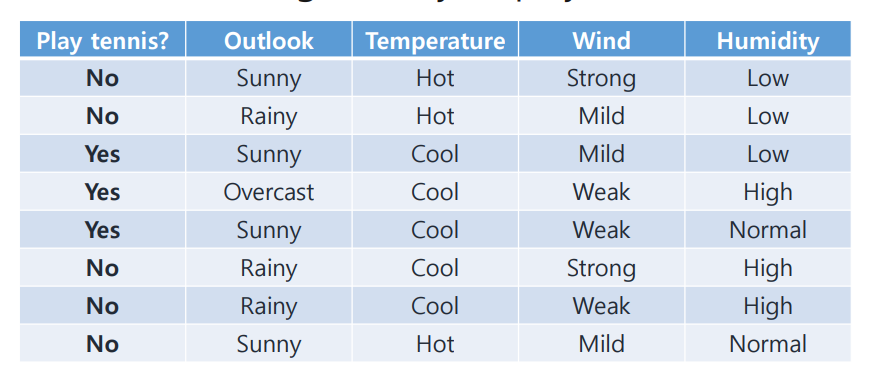
Node, 즉 분류 기준을 어떻게 정하면 좋을까? 위와 같이 discrete value를 갖는 예제의 경우, homogeneous(같은 결괏값만 나온) group을 찾는 과정을 통해 분류 기준을 정할 수 있다.

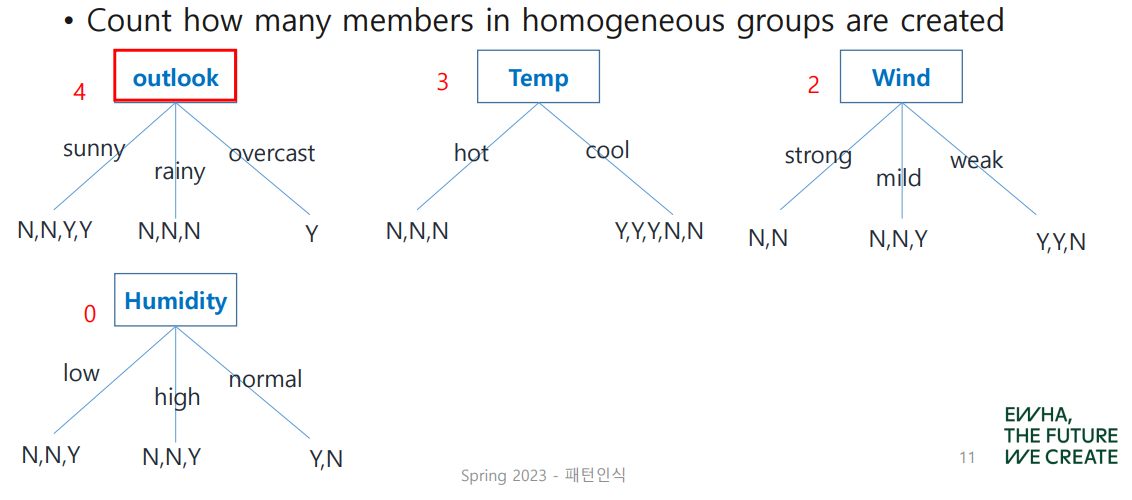
homogeneous group의 수를 셌을 때, 그 값이 가장 큰 것이 분류 기준으로서의 역할을 가장 잘 수행한다고 볼 수 있으므로 이를 root node로 설정한다. 위 예제의 경우 outlook이 될 수 있겠다!

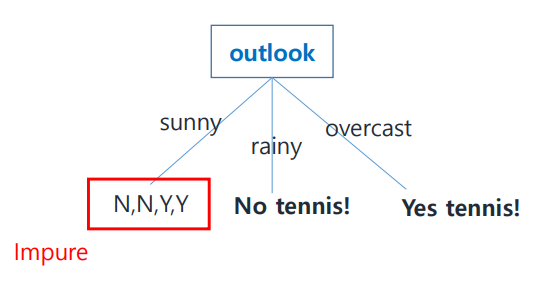
아직 불순도가 높은 group이 남아 있으므로, 이어서 node를 정해 보자. 이미 root node로 결정된 outlook을 제외하고 homogeneous group count를 시작한다.

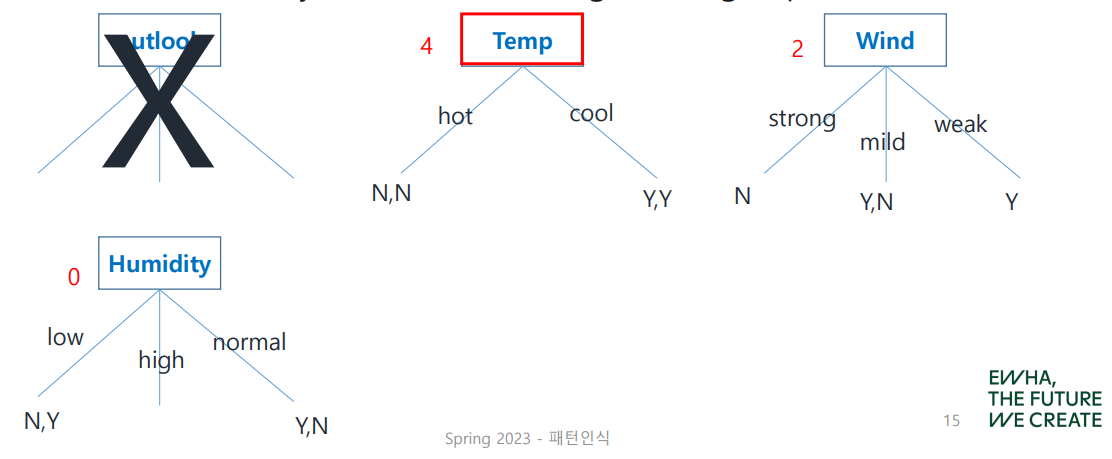
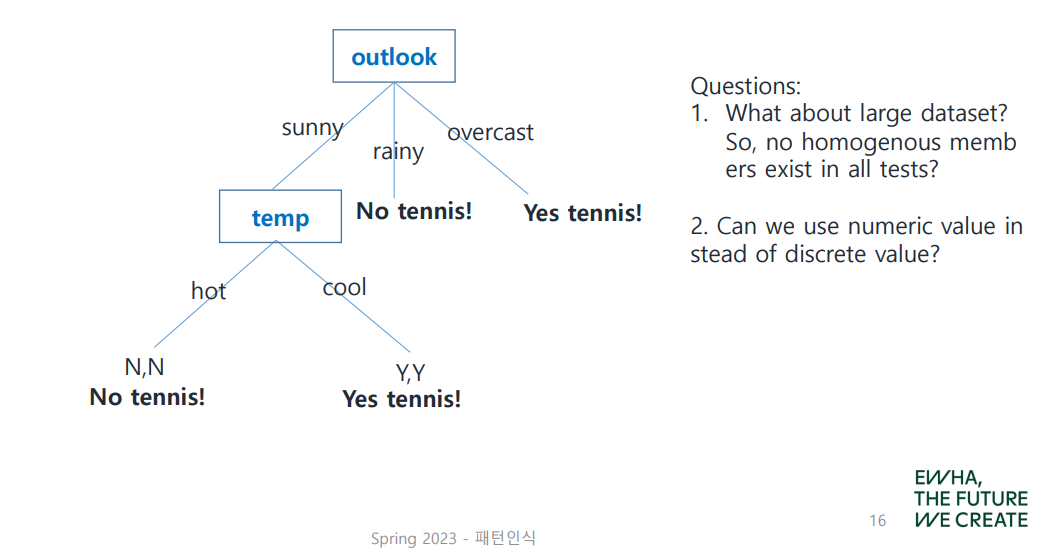
Decision Tree의 확장은 위와 같이 이루어진다. 그러나 모든 경우가 이렇게 딱딱 나누어떨어지는 것은 아니다.

Question 1?

What about large dataset?
If there are no homogeneous members in all tests?

실제 문제에서는 homogeneous group이 만들어지지 않는 경우가 다반사이다.
이와 같은 경우를 위해 불순도를 명확하게 계산할 수 있는 방법을 알아볼 것이다. (Entropy, Gini)

Entropy function

$E(x) = \displaystyle - \sum^k_{i=1}p_i \log_2 p_i$
where $p_i$ is the fraction of class $i$

아래 예시에 공식을 적용해 보자.

총 16개 중 빨간 점이 10개, 파란 점이 6개이다.
이 경우 엔트로피는 다음과 같이 계산할 수 있다.

$E = - \displaystyle \frac 6 {16} \log_2(\frac 6 {16}) - \frac {10} {16} \log_2(\frac {10} {16}) \approx 0.95$

모든 점이 한 가지 색깔뿐이라면 어떨까?

$E = - \displaystyle \frac 0 {16} \log_2(\frac 0 {16}) - \frac {16} {16} \log_2(\frac {16} {16}) = 0$

entropy가 0이므로, 불순도가 없어 가장 이상적인 상태가 됨을 알 수 있다.

앞의 테니스 예제에 적용시킨 뒤, 그래프를 통해 자세히 알아보자.

class $i$의 비율을 나타냈던 $p_i$를 테니스 예제에 맞게 설정한 공식은 다음과 같다.

$E(x) = \displaystyle - \frac Y T \log_2 \frac Y T - \frac N T \log_2 \frac N T$

($Y$: yes tennis!, $N$: no tennis!, $T$: $Y+N$)

What this point indicates? (blue point)

$\frac Y T$가 0.5인 지점에서 entropy가 1.0으로 가장 높은 것을 알 수 있다.
반대로 $\frac Y T$가 0이거나 1인, 즉 모든 sample이 1개의 클래스에만 속하는 경우 entropy는 0인 것을 관찰할 수 있다.

Q(test) in Entropy Analysis

$Q(test) = \sum_{x \ ∈ \ leaf \ node}D(x) \times \displaystyle \frac {\# \ samples \ in \ the \ leaf} {\# \ samples \ in \ test}$

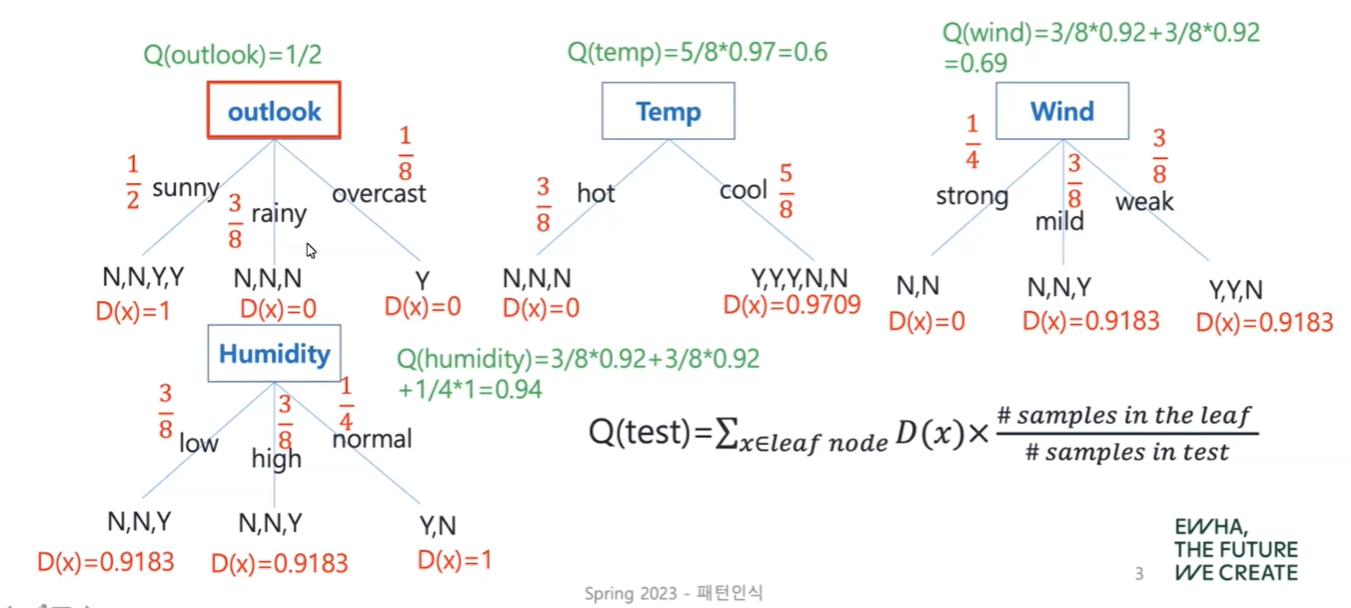
여기서 Q(test)는 quality, 즉 각각의 feature가 분류에 얼마나 도움이 되는지 알 수 있는 척도이다. 이 값이 작을수록 의미 있는 feature이다.

Gini Index

$Gini(x) = 1 - \displaystyle \sum^k_{i=1}p^2_i$
where $p_i$ is the fraction of class $i$

아래 예시에 공식을 적용해 보자.

총 16개 중 빨간 점이 10개, 파란 점이 6개이다.
이 경우 Gini Index(지니 계수)는 다음과 같이 계산할 수 있다.

$G = 1 - \displaystyle (\frac 6 {16})^2 - (\frac {10} {16})^2 \approx 0.47$

모든 점이 한 가지 색깔뿐이라면 어떨까?

$G = 1 - \displaystyle (\frac 0 {16})^2 - (\frac {16} {16})^2 = 0$

지니 계수가 0이므로, 불순도가 없어 가장 이상적인 상태가 됨을 알 수 있다.

마찬가지로 앞의 테니스 예제에 적용시켜 보자.
class $i$의 비율을 나타냈던 $p_i$를 테니스 예제에 맞게 설정한 공식은 다음과 같다.

$Gini(x) = 1 - \displaystyle (\frac Y T)^2 - (\frac N T)^2$

($Y$: yes tennis!, $N$: no tennis!, $T$: $Y+N$)

본 예제에서는 entropy 공식을 적용했을 때와 Gini impurity를 이용했을 때의 값이 같(은가??)지만, 다르게 나올 수도 있다.

Q(test) in Gini Impurity

$Q(test) = \sum_{x \ ∈ \ leaf \ node}Gini(x) \times \displaystyle \frac {\# \ samples \ in \ the \ leaf} {\# \ samples \ in \ test}$

마찬가지로 여기서도 Q(test)는 quality, 즉 각각의 feature가 분류에 얼마나 도움이 되는지 알 수 있는 척도이다. 이 값이 작을수록 의미 있는 feature이다.

Question 2?

Can we use numeric value instead of discrete value?
실수로 이루어진 수치 데이터를 어떻게 Decision Tree로 분류할 수 있을까?

그 해답은 예제를 통해 알아보자.

How to handle numeric value

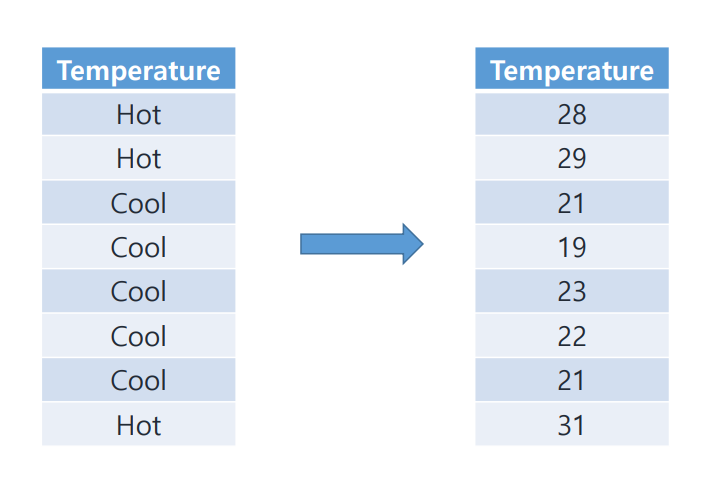
더운지, 추운지와 같은 discrete value가 아닌 실제 온도(numeric value) 데이터를 분류하는 방법은 무엇일까?

1. 값 정렬하기

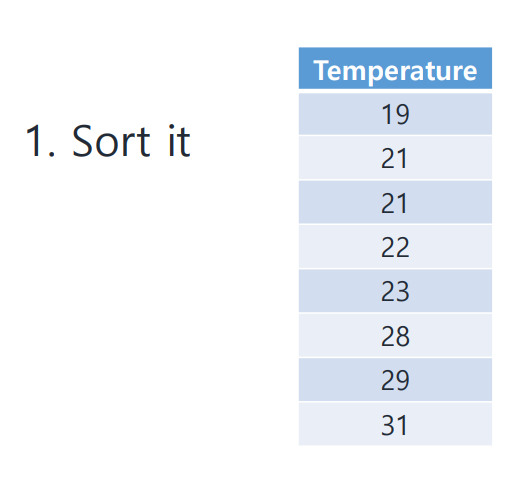
우선 데이터를 크기 순으로 정렬(sort)한다.

2. Split Point 찾기

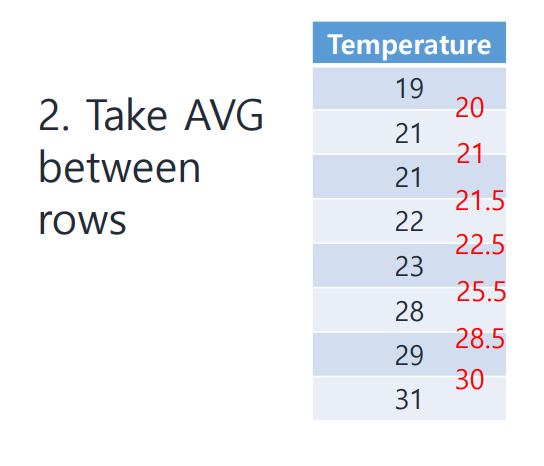
이번 예제의 경우 split point를 찾기 위해 각 value 간의 AVG(평균)을 사용하였으나, 다른 값을 사용할 수도 있을 것이다.

3. Split Point 적용시켜 보기

찾아낸 split point를 node로 만들어 적용시켜 본 뒤, entropy나 gini impurity를 계산하여 그 값이 가장 작게 나오는 feature를 선택한다!

이 개념을 적용시켜 Regression Tree를 알아보자.

Decision Trees for Regression

수면 시간과 생산성의 관계에 관한 예제이다.
이 data plot은 Linear Regression을 적용시키기 어려워 보이므로,
앞서 배운 과정대로 Regression Tree를 사용해보자. 우선 적절한 split point를 찾는 것이 중요하다.

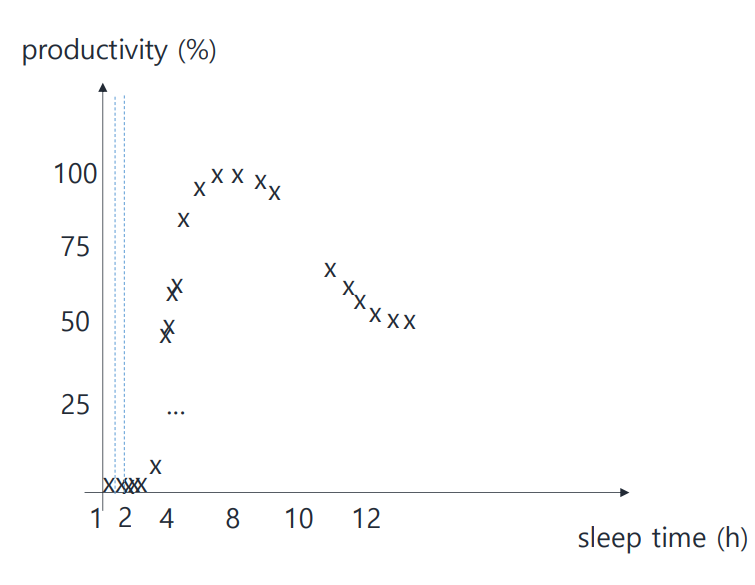
만약 split point를 위와 같이 약 1.5로 설정했다면 어떨까?
좀 아닌 것 같지 않은가?! 두 번째 split point 이후 값들의 variance가 너무 크므로 tree size가 쓸데없이 방대해질 것이다.

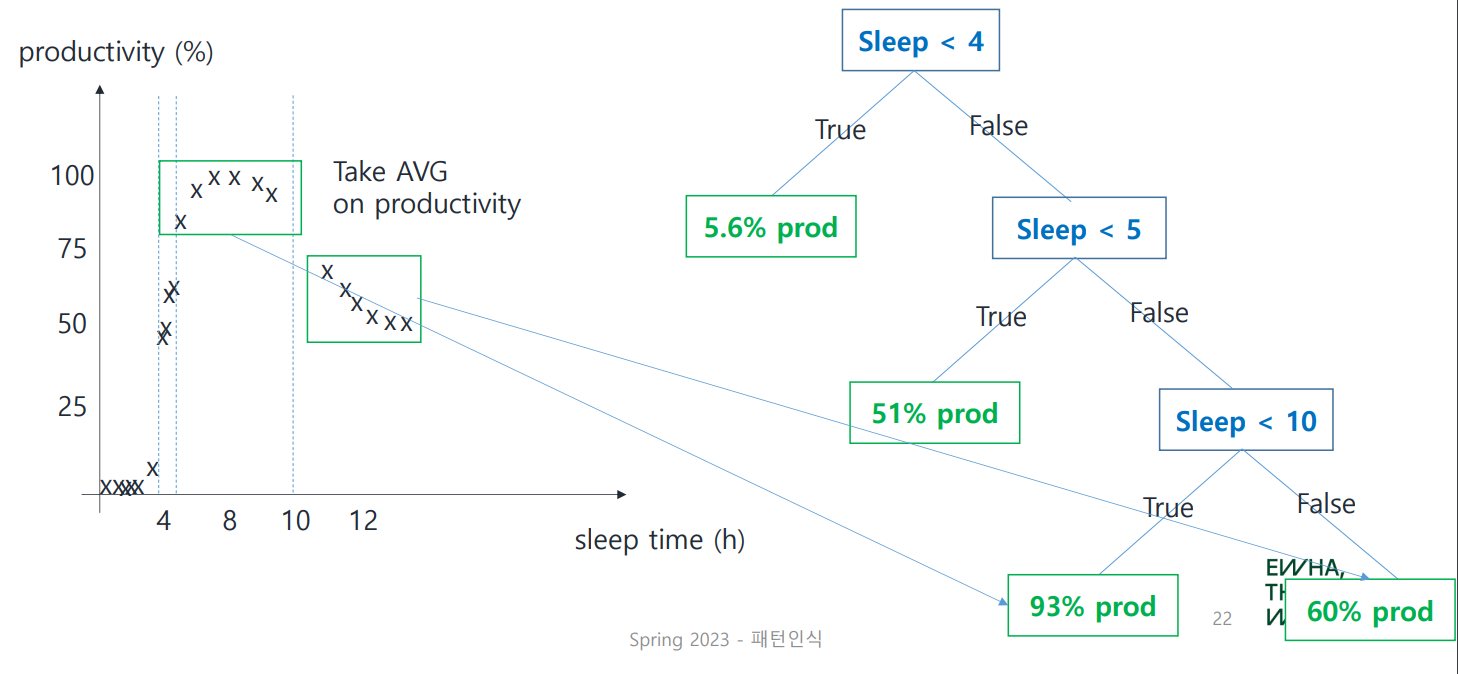
위 그림은 어떤가?
아까보다 잘 나눠진 것을 확인할 수 있다. 초록색 박스와 같이 data가 모여 있는 곳을 Cluster라고 한다. split point를 설정할 때에는 이렇게 cluster를 잘 구성하도록 계산할 필요가 있다.

다음 공식을 통해 밀집도를 파악하여 이용할 수 있다.

Compute Sum of Squared Residuals

$\sum_{x_i \ ∈ \ R_p}(y_i-c_p)^2 + \sum_{x_i \ ∈ \ R_n}(y_i - c_n)^2$

$c_p = average(y_i | x_i ∈ \ R_p)$ (positive)
$c_n = average(y_i | x_i ∈ \ R_n)$ (negative)

위 공식은 설정된 split point로 인해 만들어진 두 group(positive, negative)의 밀집도를 나타내며, 그 값이 작을수록 밀집도가 크다.

왜 작을수록!?

$y_i - c_p$는 평균과의 거리를 나타내므로, 각각의 productivity들이 밀집되어 있을수록 그 값이 작게 나타날 것이다!

split point를 1.5로 설정했을 경우에 이 공식을 적용시켜 보자.

False group에 속한 값들의 평균은 39%이다.
앞선 공식을 적용시킨 값이 한눈에 봐도 개~ 커 보인다.

정리하자면...

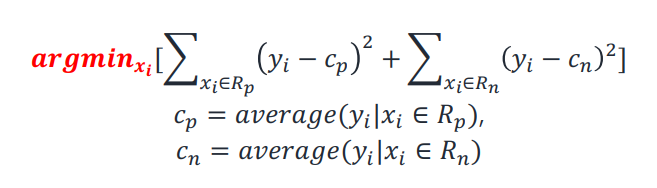
split이 초래하는 두 $R_p, R_n$의
각각의 인스턴스들의 거리가 좁을수록 좋은 split 지점이 된다!

Decision Tree에서 일어나는 Overfitting에 관해서도 알아보자.

Overfitting in Decision Trees

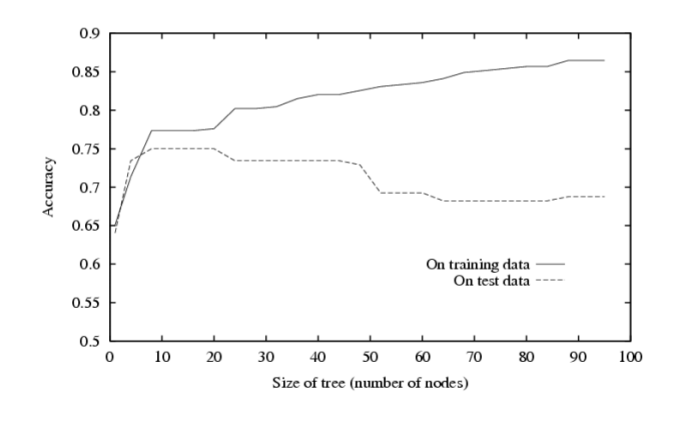
위 그래프는 Size of tree(number of nodes)에 따른 training data와 test data의 Accuracy이다.

• train: tree size가 커질수록 정확도도 계속 증가한다.
  (node가 많아질수록 homogeneous 그룹이 생길 가능성이 높아지기 때문)
• test: 약 20 이후로는 정확도가 감소한다!

training data의 error rate를 $error_{tr}(h)$,
testing data의 error rate를 $error_{te}(h)$라고 할 때,

Overfitting이 일어나는 지점은?

$error_{te}(h) > error_{tr}(h)$

Overfiting의 amount는?

$error_{te}(h) - error_{tr}(h)$
즉, training data와 testing data의 error rate의 gap이다.

---

Avoid Overfitting

I can avoid it.#φωφ
이때 overfitting을 견제하는 방법은 크게 두 가지로 나눌 수 있다.

Pre-pruning (Early Stopping)

split point를 더 추가하는 것이 의미가 없다고 (statistically insignificant) 판단되면, tree size를 확장시키는 것을 임의로 멈추는 방법이다.

Post-pruning

계속해서 tree size를 확장시킨 뒤 (allow overfitting) 추후에 pruning을 진행하는 방법이다.

post-pruning의 한 방법으로 Reduced Error Pruning이 있다.

Reduced Error Pruning

Leaf Node에서부터 거슬러 올라가며, Validation Set을 활용하여 각 노드를 제거했을 때의 정확도를 계산하고 이를 가장 높게 하는 노드를 제거한다.

다음 예제로 살펴보자.

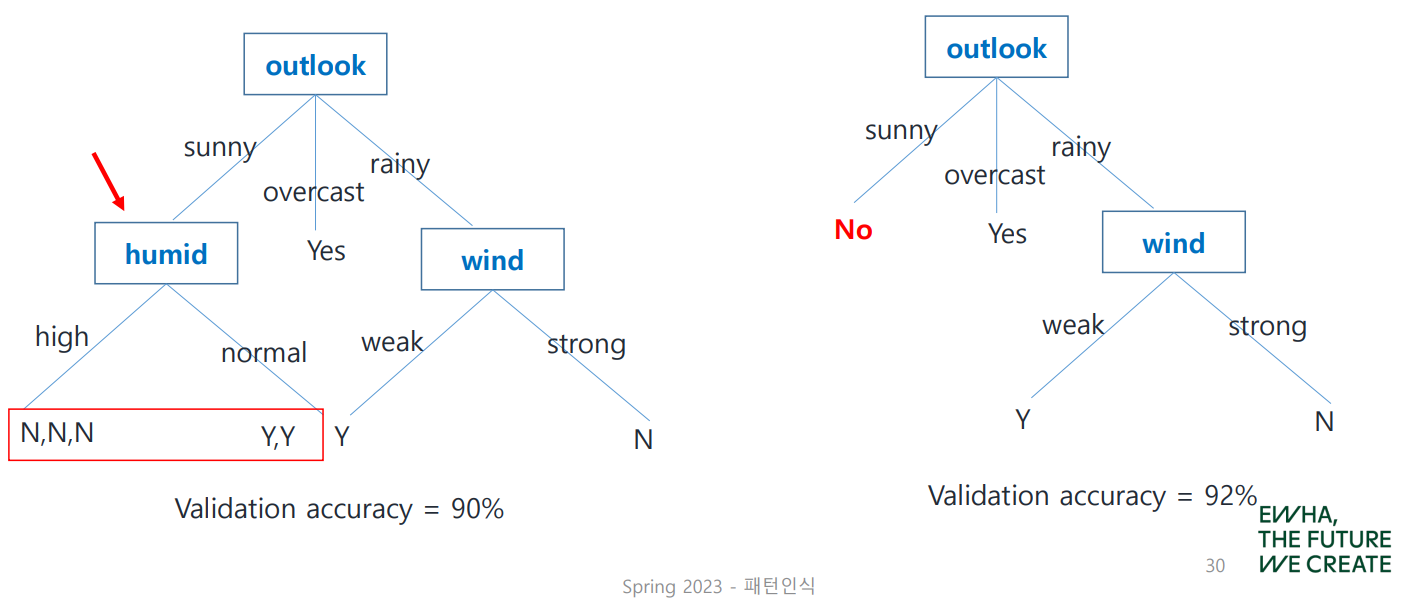
humid node를 없애면 Validation Accuracy가 2% 증가하므로 이를 제거하게 되는데, 이때 Y보다 N이 common하므로 node가 사라진 자리에 No가 들어간다.

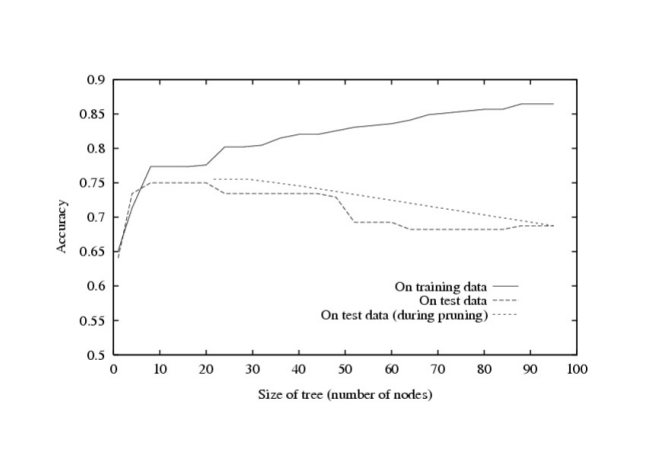
이와 같이 pruning을 진행하더라도 Overfitting을 완전히 해결할 수는 없기에, 조금 줄이는 정도에 그치는 것을 확인할 수 있다.

다음 글에서는 Decision Tree Algorithm을 실제 코드로 살펴보자.