🐱‍🏍 Classification

decision boundary를 찾아가는 과정!

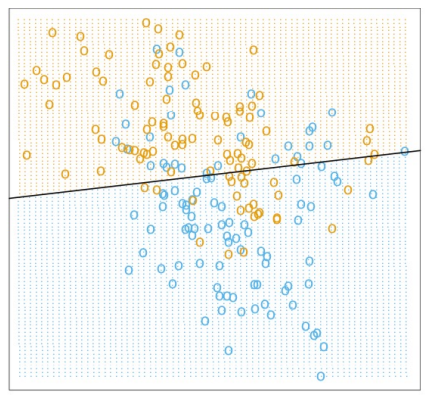
ex) 위 그림의 경우 output이 둘로 나뉘어지므로 binary classification이다 ....

spam detection을 예시로 들어보자.

• $x_i$: features extracted based on the i-th email
• $y_i$: label
  • 1: if the i-th email is spam (positive)
  • 0: otherwise (negative)

이와 같은 경우 label인 $y_i ∈ \{0, 1\}$이므로, hypothesis function $f(x)$를 binary classification problem에 적용시킬 수 있도록 바꿔줘야 하는데...

🐱‍🏍 Logistic Regression

hypothesis function에 sigmoid function을 취해서 0~1 사이 값만 뱉어내게 하자!

$f(x) = g(β^Tx) = \displaystyle \frac 1 {1+e^{-β^Tx}}$

in which $β^Tx = β_0 + \sum^p_{j=1}β_jx_j$

✔ Sigmoid Function

The logistic function in linear regression is a type of sigmoid!

$g(x) = \displaystyle \frac 1 {1+e^{-x}}$

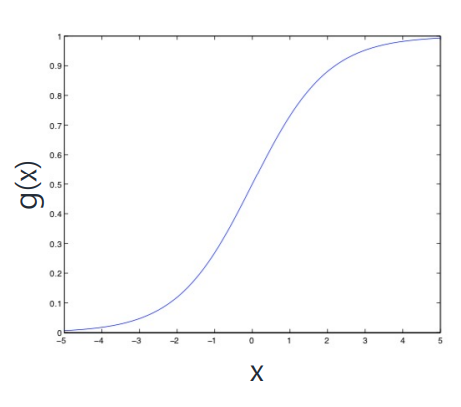
Why Sigmoid?

여백이 부족하여 적지 않겟다.
optimization은 미분의 과정을 거치는데, sigmoid function을 미분한 form이 예뻐서... 그 이유 하나뿐인 건 아니지만 ( $g'(x) = g(x)(1-g(x))$ )

✔ Likelihood of β

Assume that

• $P(y=1|x;β) = f(x)$
• $P(y=0|x;β) = 1 - f(x)$

$⇒$ 일반화하면, $p(y|x;β) = (f(x))^y(1-f(x))^{1-y}$ !!

것보다 확률밀도는 지난번에 햇던 건데 내가 까먹었구나

🐱‍🏍 Gradient Ascent

🐱‍🏍 Generative Learning Algorithm