Problems in Decision Trees
Decision Tree는 Overfitting이 일어날 수밖에 없으며, 그 해결책으로 제시된 Pre-pruning과 Post-pruning도 완전하지 않다. 그렇다고 expansion을 안 시킬 수도 없는 노릇이니 근본적인 대책이 필요한데...
아래의 두 가지 방법 모두 tree를 여러 개 만든다는 공통점이!
✔ Resolution 1: Bagging
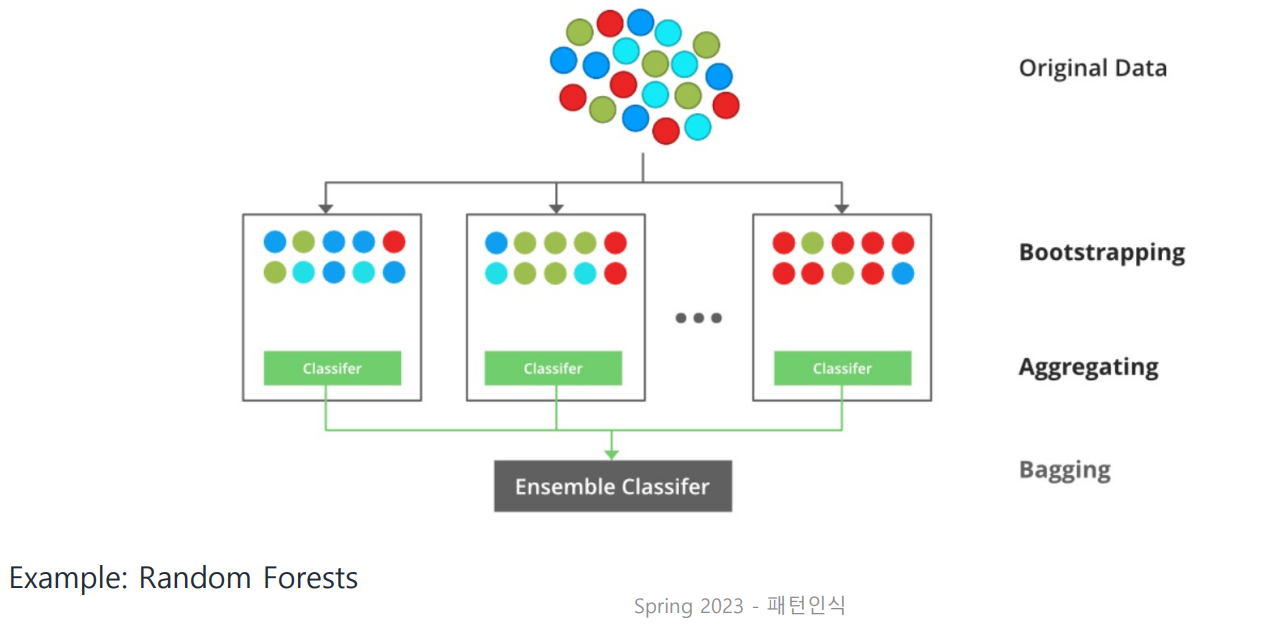
Bootstrapping
original data를 쪼개 여러 개의 subset(Bootstrap Data)을 만들고 이를 이용해 tree를 만드는데, 이때 tree들의 다양성이 중요!
feature의 개수는 제한되어 있으므로 다양한 tree를 도출해내기 위해(다양성을 보장하기 위해) Bootstrap Data를 잘 만들어야 한다!
Aggregating
다양한 tree들의 결정을 함께 고려하여 최종 예측값을 결정
앞서 만든 여러 개의 tree가 뱉어내는 모든 output을 어떻게 통합할 것인지...
- Regression 문제: Average! (평균)
- Classification 문제: Voting! (최빈값, Majority Vote값)
Bagging의 대표적인 예시로 Random Forest가 있다.
Random Forest for Regression & Classification
Goal: decision tree algorithm의 Variance를 줄이기!
(= tree 간의 correlation 줄이기, independence 높이기)
(Overfitting이 low bias, high variance에서 발생하므로.)
-
B개의 tree 생성
- feature, sample을 랜덤하게 뽑아 bootstrap data 생성
(select variables at random from the variables, ) - 각 bootstrap data로 tree를 구축, forest를 만듦
- feature, sample을 랜덤하게 뽑아 bootstrap data 생성
-
만들어진 tree ensemble(표기: )로부터 결과 종합
- Regression: Averaging!
- Classification: Voting!
Recommendations for m
- Regression:
- Classification:
랜덤 포레스트를 직접 만들어 보자.
Construct Random Forest
1. Create Bootstrapped Data
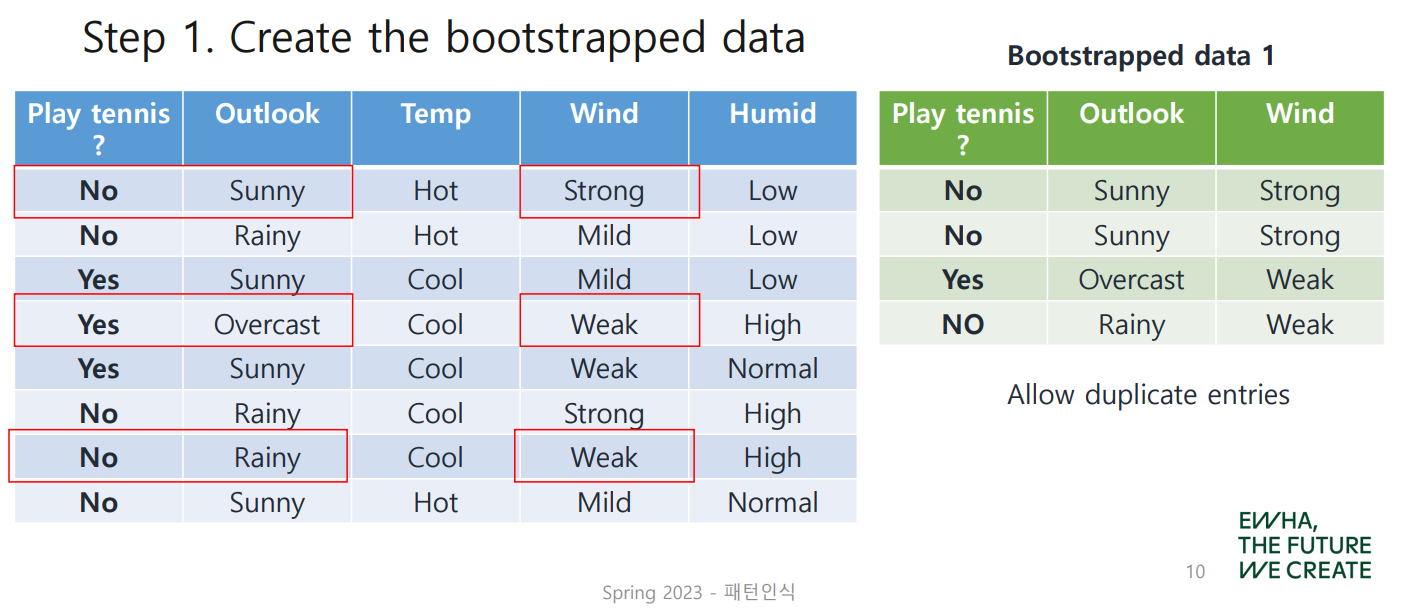
feature, sample을 랜덤하게 골라 Bootstrap Data를 만들었다.
중복(overlap)이 가능하다는 점에 유의!
2. Grow Decision Trees
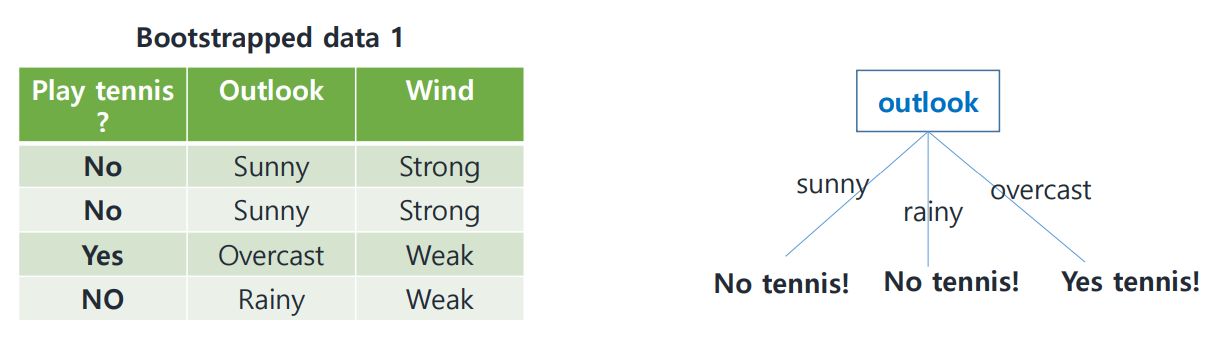
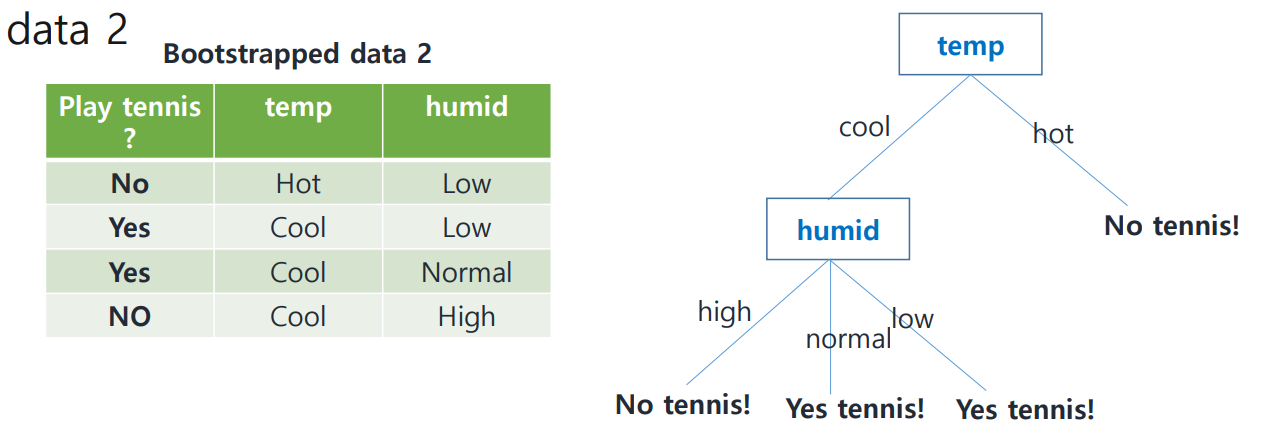
homogeneous group만 남을 때까지 tree를 확장하였다.
이 과정을 반복하며 B개의 tree를 만들자...
3. Repeat 1&2 to construct B trees
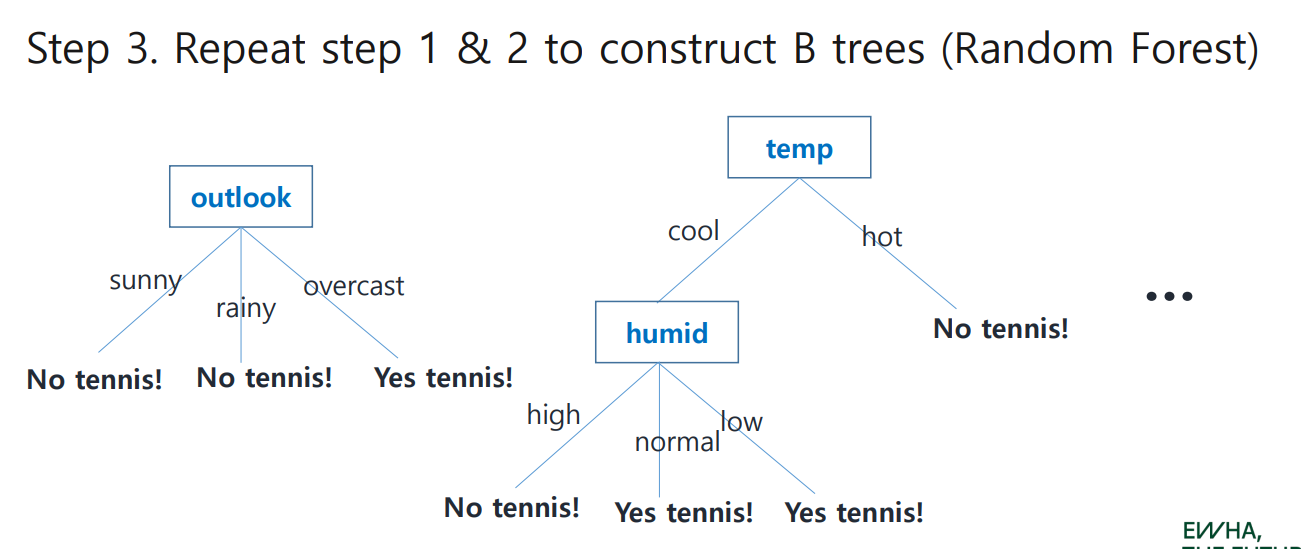
4. Feed Testing Data and Aggrregate Results from each tree
testing data를 이용해서 모든 tree를 traverse하는 과정이다.
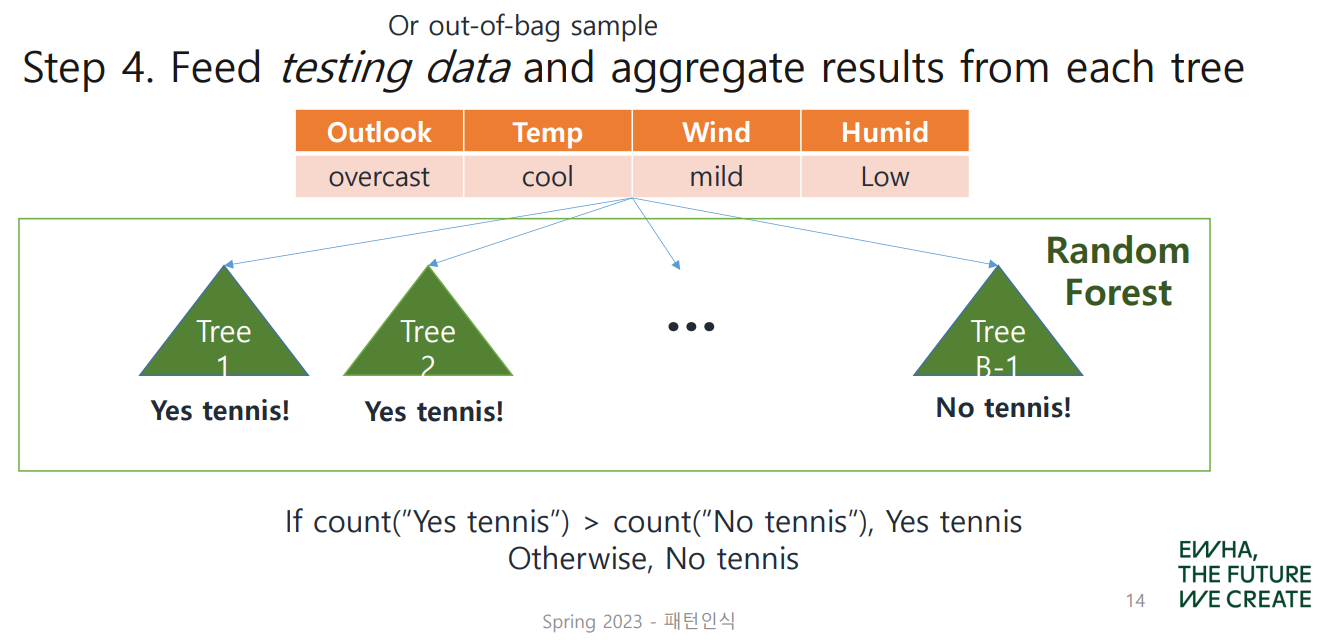
Yes tennis가 결괏값으로 출력된 경우가 더 많다면,
Yes tennis가 majority vote, 선택된다!
헌데 이 경우 testing data로는 무엇을 이용할까?
Out-of-bag (OOB) Error
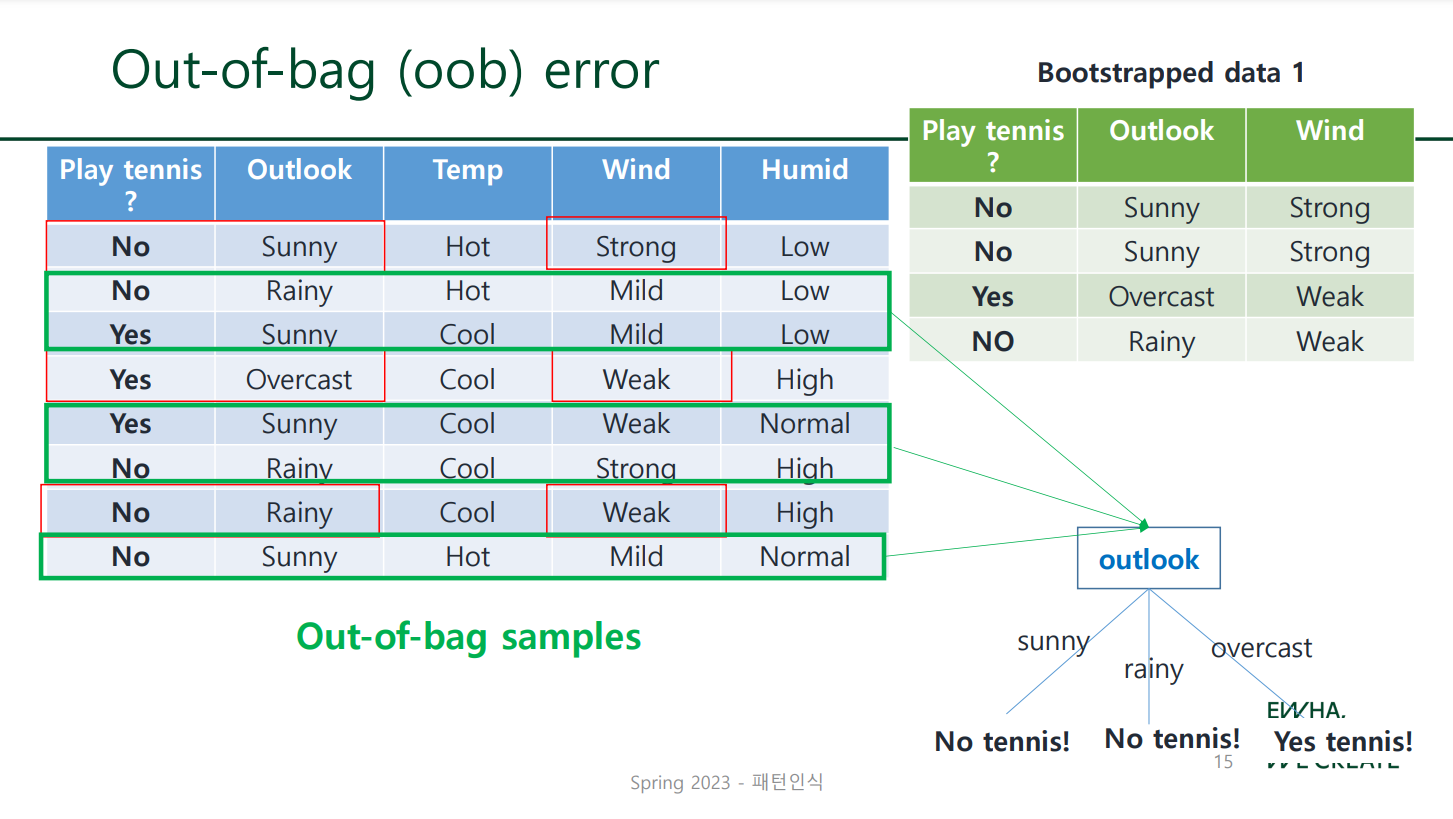
Bootstrap Data를 만들고 남은, 선택되지 않은 sample들을 Out-of-bag Sample이라고 하며, 이를 성능 측정 과정에서 testing data로 이용한다.
tree가 여러 개다 보니, 어떤 tree에서는 OOB data인 것이 다른 tree에서는 그렇지 않을 수도 있으므로 이를 구분하여 OOB data일 경우에만 testing data로 이용, feed해야 한다.
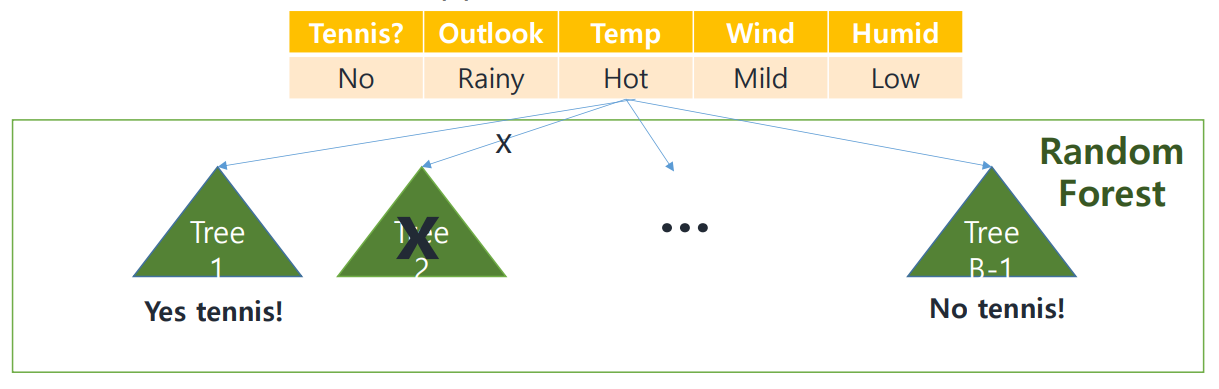
Empirical Observations
Decision Tree와 Random Forest의 특징들이라고 이해하면 될 듯하다.
- 각각의 tree는 overfit될 가능성을 늘 지니고 있다. 확장할수록 overfitting 일어날 확률은 높아지는데 그렇다고 확장을 안 할 수 없기에...
- 그러나 구축한 forest에 충분히 많은 수의 tree가 있다면 overfitting되지 않는다!
- 적어도 2,000개 이상의 tree가 만들어지는 것이 좋음.
- forest 내 각각의 decision tree가 효과적일수록 random forest의 성능도 좋아진다! (각 tree의 error가 낮을수록 forest의 에러 또한 ↓)
- 어느 feature의 성능이 가장 좋은지 판단하도록 해 주는 coefficient가 따로 제공되지는 않는다.
그렇다면 Random Forest 모델링에서는
각 variable(feature) importance를 어떻게 알아볼 수 있을까?
Variable (Feature) Importance
1. Gini Importance
앞서 배운 Gini Index로 각 노드의 Impurity를 계산하여 그 차(gap)의 평균을 구하는데, 이 값이 클수록 그 feature는 중요하다는 뜻이 된다.
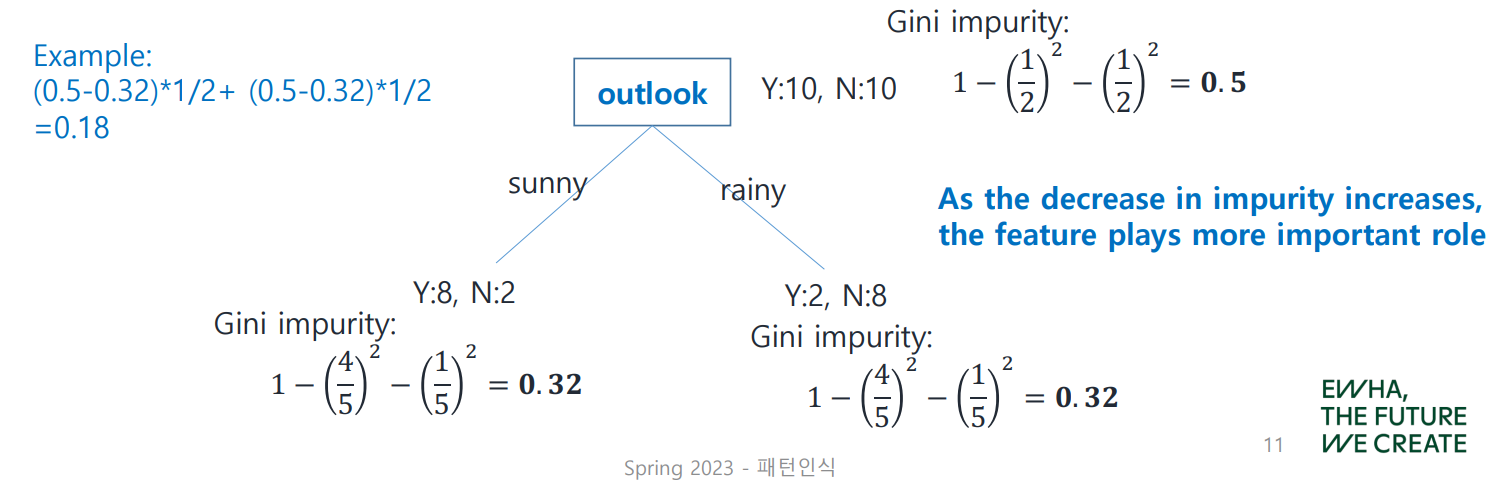
위 그림에 따르면, outlook이라는 feature의 gini importance는
이다.
2. Permutation Importance (Randomization)
모델의 정확도를 측정한 후, 특정 열(feature)의 데이터를 shuffle하고 다시 정확도를 측정해 그 차이를 알아본다. 데이터를 섞는 것은 다시 말해 해당 feature가 기능을 못하도록(의미를 잃도록) 만드는 것이며, accuracy의 차이가 클수록 해당 feature가 중요하다는 뜻!
참고로 accuracy를 측정하든 error을 측정하든 성능 평가할 수 있는 지표라면 뭐든 가능하며, Gini보다 이쪽이 더 많이 쓰이고 작동도 잘한다고.
Hyperparameters in Random Forests
Random Forest 모델링을 할 때 정해주어야 하는 값은 무엇이 있을까?
-
Decision Tree 개수
-
Bootstrap 데이터 생성 시 feature의 개수 ()
어떤 것이 좋을지는 case by case이므로, 각각의 경우 효과적인 값을 찾는 것이 중요하나 일반적으로 다음과 같은 특징을 갖는다.- : bootstrap data 간 유사성이 증가하여 각 tree 모습도 비슷해지며, 특정 feature가 강조될 수 있다.
- : randomness가 보장된다.
-
Decision Tree 생성 관련 변수
- Max Depth
- Min Sample Count
✨ 이건 개인적으로 정리하는 건데
Parameter?
모델링을 통해 자동으로 결정되는 값
Hyperparameter?
모델링할 때 사용자가 직접 정해주어야 하는 값
random forest를 만들려는데 missing data가 있다면 어떻게 해야 할까?
How to handle missing data
Missing columns in training data
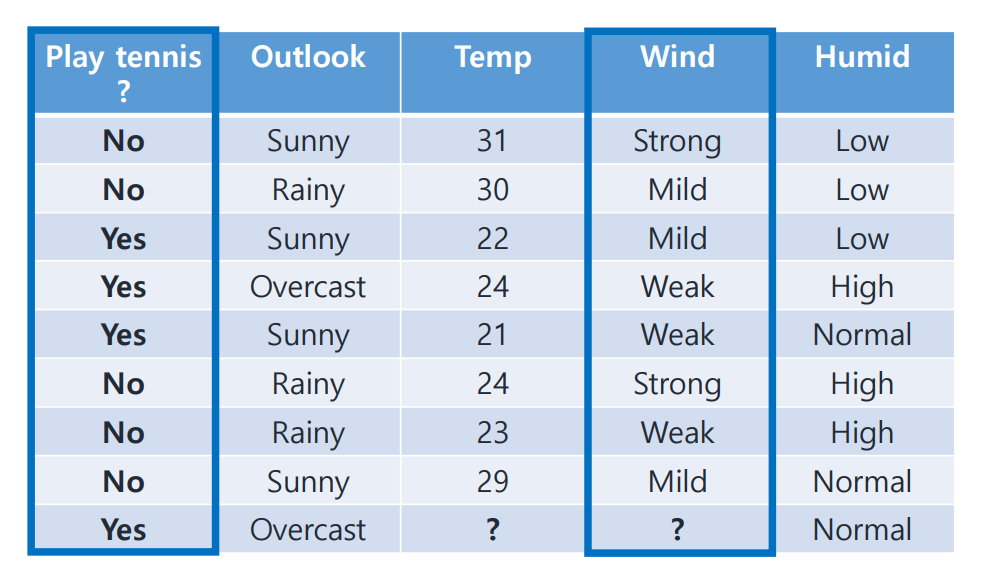
Temp, Wind column의 값들이 하나씩 missing되어 있다.
Average(평균)와 Vote(빈도)를 이용할 수 있다!
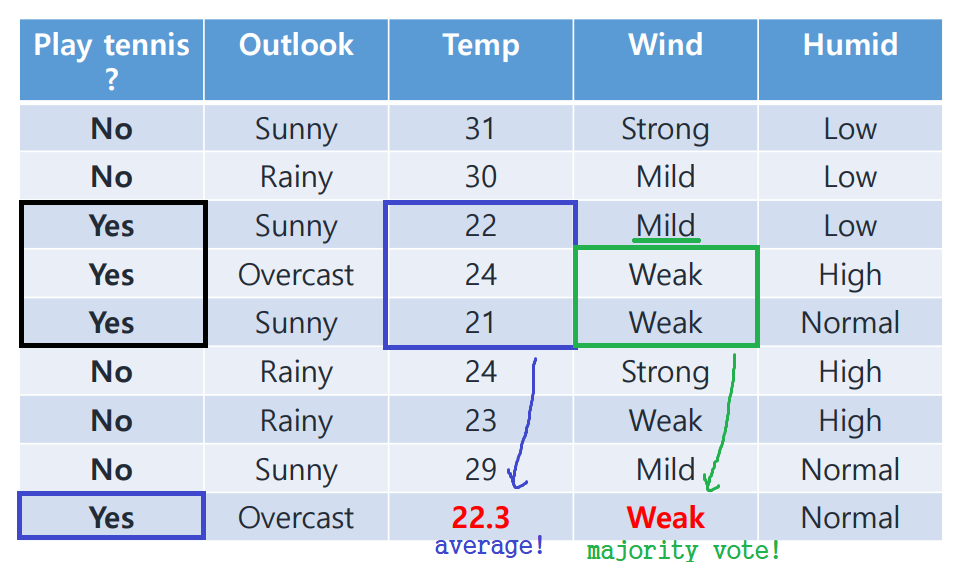
새로 넣은 값이 합당한지 실험적으로 검증하기 위해 Similarity Table을 만들어 보자!
Derive Similarity Table
위 데이터를 쪼개어 만든 10개의 tree가 있다고 가정하자.
이 각각의 tree에 모든 sample을 한 줄(row)씩 feed해 본다.
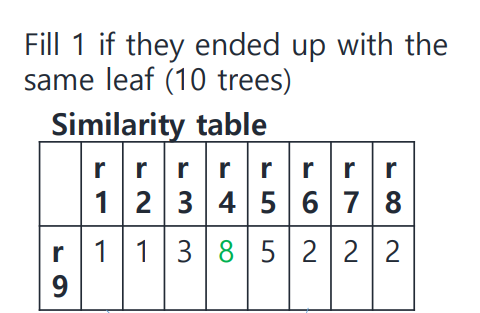
missing value가 존재하는 r9(9번째 행)을 기준으로 살펴보자. r9를 제외한 8개의 row를 모두 feed했을 때, r9와 같은 결괏값이 나온 tree의 개수를 세어 적는다.
ex) 위 표를 보면 r4, r9는 8개의 tree에서 같은 결과를 도출하였다. (이를 두 row의 similarity가 높다고 말한다.)
이 Similarity Table을 가중치로 이용하여 missing data에 적합한 값이 무엇인지 도출해낼 수 있다.
Refine 'Wind' value
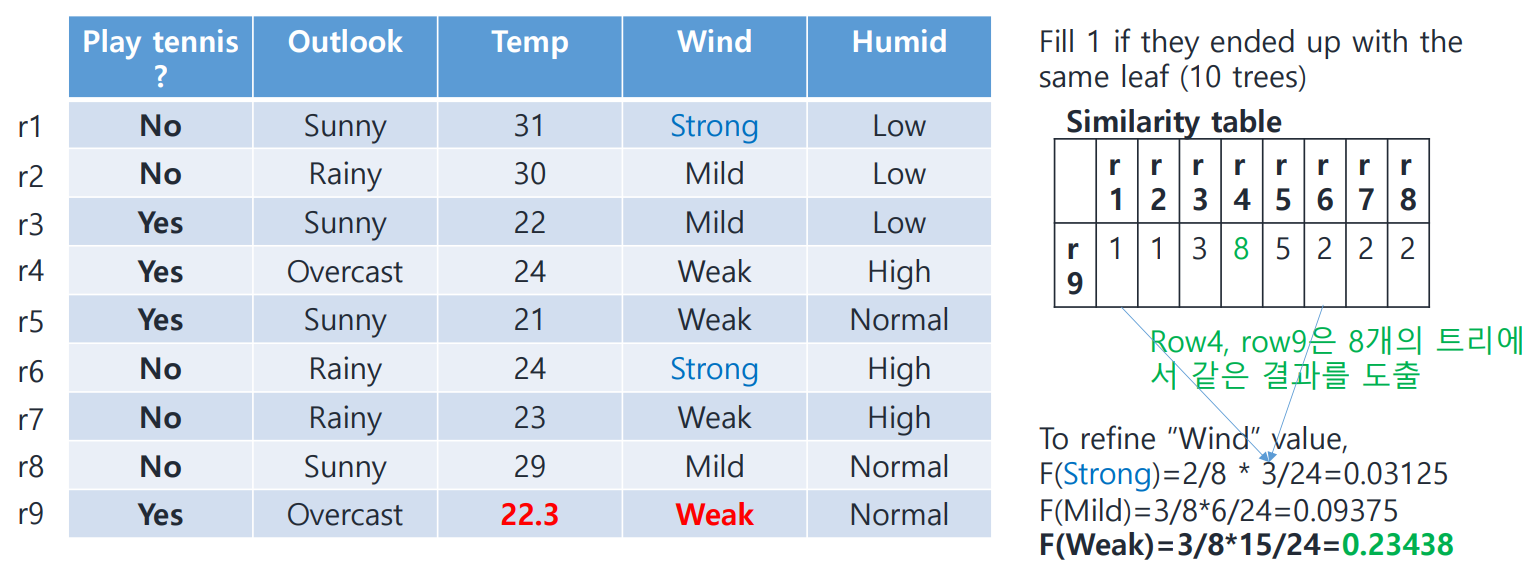
Strong은 적합한 값일까?
- r1~8에서 Strong은 2번 나왔다. ()
- Strong이 나온 row인 r1, r6과 r9의 similarity를 더해 24(Similarity Table에서 숫자들의 총합)로 나눈 값을 가중치로써 곱한다. ()
이런 식으로 Strong, Mild, Weak 각각의 적합도(적합도라 부르는 게 맞나?)를 계산해 보니, Weak의 값이 가장 높다! (Weak가 가장 유력함)
Refine 'Temp' value
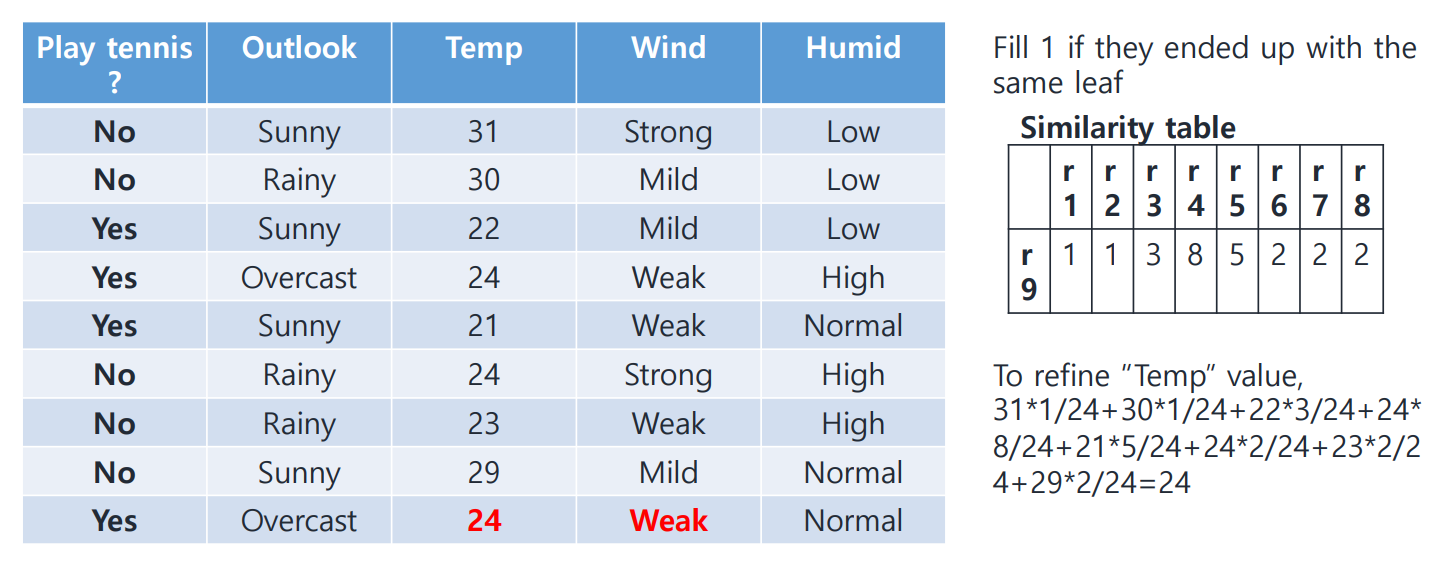
Temp feature에 해당하는 값들에 가중치를 곱해 모두 더하니 24가 나온다.
Missing columns in testing data
testing data의 경우도 비슷하게 진행되나, training data의 missing value를 채우는 경우가 더 많긴 하다고.

이 경우에는 Label(Yes tennis인지, No tennis인지)도 안 주어진 상태!
- training data 때와 마찬가지로 similarity table을 만들고 가중치를 이용하여 temp value를 refine하는 방식을 사용한다.
- Yes label, No label이 달린 두 testing data를 모두 random forest에 feed해 본 뒤, 더 많은 vote를 얻은 쪽으로 label을 선택한다!
✔ Resolution 2: Boosting
Bagging은 각 tree 간의 순서랄 게 딱히 없는 데 반해, (parallel)
Boosting의 tree들은 순차적으로 되어 있다.
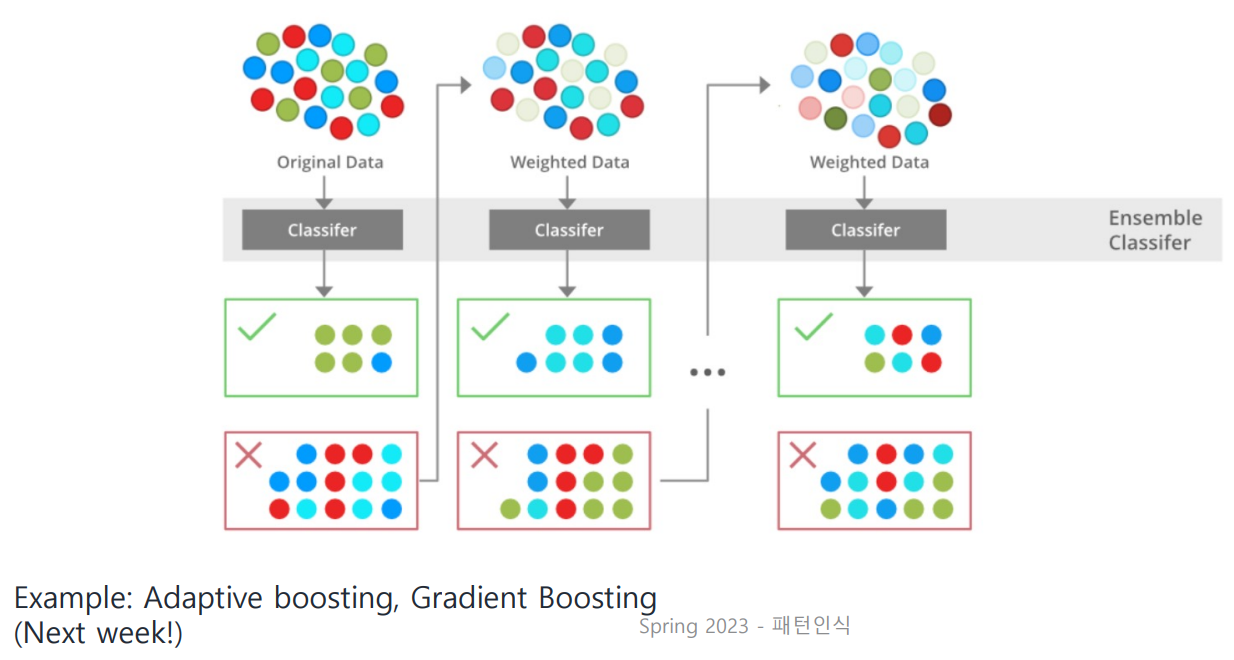
매 tree 형성 시 이전 tree에서 분류하지 못한 것(Misclassification)을 다음 tree에서 제대로 분류하겠다는 목표가 존재한다!
Boosting에는 Adaptive Boosting(Adaboost), Gradient Boosting의 두 가지가 존재한다.
Adaboost
- weak learner(stump)들의 결합으로 이루어져 있다.
- 각각의 learner에는 서로 다른 weight가 붙는다.
- 각각의 sample에 또한 서로 다른 weight가 붙는다.
- latter learner는 former learner의 취약점을 극복하는 쪽으로 학습되므로, former learner의 misclassified sample에 초점을 맞추게 된다! (weight를 조절함으로써)
Stump?
depth가 1이며 child node가 2개인 가장 단순한 형태의 tree
Adaboost Algorithm
Adaboost Algorithm의 작동 과정을 알아보자.
(근데 그럼 이 예제는 classification에 관한 건가 adaboost가 regression에도 적용될 수는 있는 것 같은데 그냥 이것만 다루신 건가)
-
각 sample에 대한 첫 weight()는 다음과 같이 설정한다.
-
개의 stump에 대하여 :
- 를 사용해 training data로 classifier 를 학습시킨다.
- 각 stump의 성능을 다음과 같이 평가한다. (accuracy, error 모두 가능하나 본 예제에서는 error 사용)
- 앞의 을 이용하여 특정 stump에 대한 weight()를 다음과 같이 설정한다.
- 앞의 을 이용하여 를 다음과 같이 update한다.
-
결과값으로 predicted label(1 or -1)을 뱉어내는 함수 를 다음과 같이 정의한다.
이때, 는 1과 -1만을 뱉는다고 가정한다.
처음 보는 함수들을 설명을 좀...
?
Indicator Function
괄호 안의 식이 참일 경우 1, 거짓일 경우 0을 뱉는다.
ex) 위 경우, , 즉 misclassification인 경우 1을 뱉는다.
?
괄호 안의 식이 양수일 경우 1, 음수일 경우 -1, 0일 경우 0을 뱉는다.
다 쓰기는 햇다만 이해가 진짜 하나도 안 가므로
예제를 통해 알아봅세다.
Adaboost Algorithm example!
우선 각 sample에 대한 initial weight를 1/8로 설정한다.
(Initial weight = 1 / #samples)
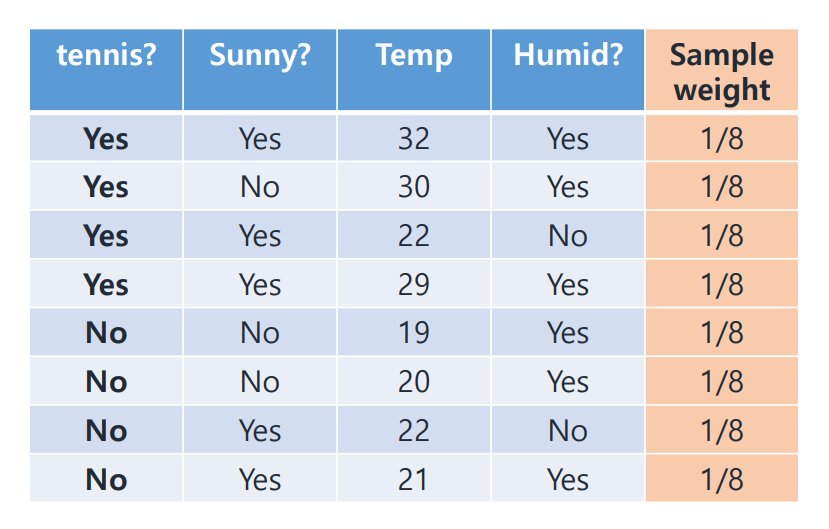
Stump를 만들어 보자.
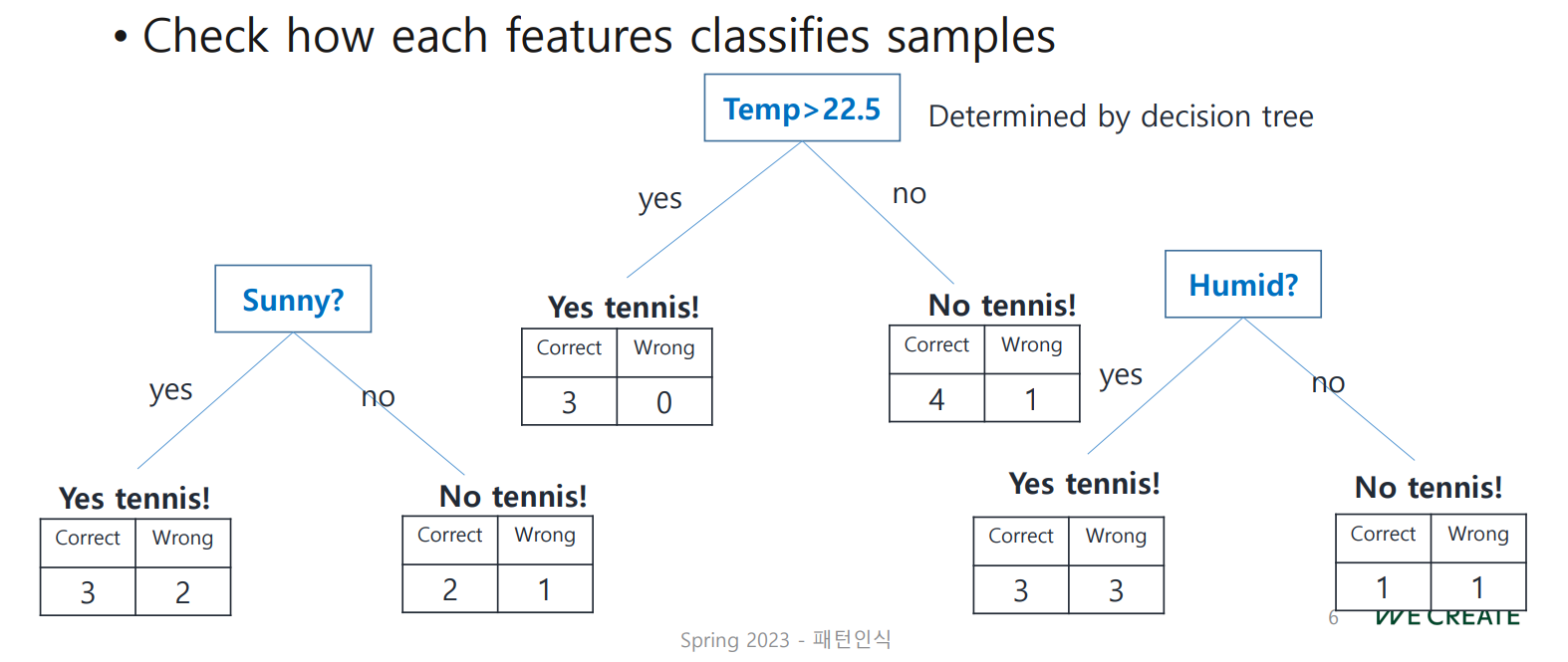
각 stump의 불순도를 계산하여, 개중 가장 잘 classify된 (불순도가 가장 작은) node를 선택한다.
Gini Impurity, Entropy 모두 사용 가능하나 여기서는 지니를 이용함!

해당 stump에 대한 weight를 계산하자. ()

를 이용해 를 update한다.
이전 tree에서 misclassification이 일어난 부분에 초점을 맞춰야 하므로, 다음과 같이 계산할 수 있다.

새로운 를 어떻게 이용할 수 있을까?
- 정규화!
- Gini Impurity 계산 시 이용하거나, sampling에 이용!
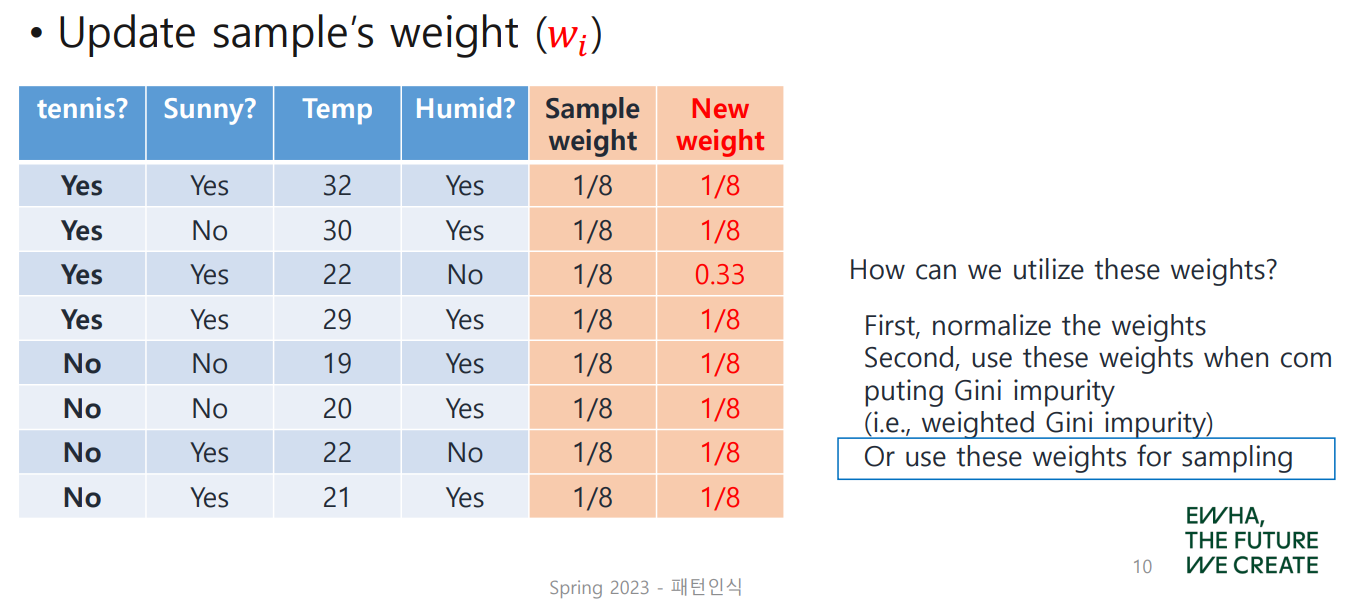
여기서는 새로운 weight를 정규화한 뒤 sampling에 이용하는 방법이 나와 있다. 새로운 weight는 sample을 pick할 때 확률로 이용되어, misclassificaiton을 일으킨 sample이 더 잘 고려되도록 할 수 있다. (weighted random)
아래 표를 보면 세 번이나 뽑혀 있는 것을 볼 수 있다.

위 과정을 반복하여 forest of stumps가 구성되면, 각각의 stump에 testing data를 feed하여 aggregate 과정을 진행한다. 아래 그림에서 각 stump(삼각형)는 weight를 고려하여 classification이 잘 되는 것이 크게 그려져 있다.
앞의 식으로 인해 결괏값으로는 1과 -1만이 출력되며, majority vote인 것을 최종 예측값(final prediction)으로 선택한다!

Gradient Boosting에 대해 알아보자.
Adaboost와 Gradient Boosting은 대체로 비슷하나, 다음과 같은 차이점을 갖는다.
Adaboost vs. Gradient Boosting
- stump를 이용하는 Adaboost와는 달리, Gradient Boosting은 actual tree를 이용하며 그 대신 leaf node 수에 제한을 둔다.
- Gradient Boosting은 leaf에서부터 시작한다!
regression과 classification 둘 모두에 적용시킬 수 있으나, 본 수업에서는 regression만 다룬다.
Gradient Boosting Algorithm for Regression
Gradient Boosting Algorithm의 작동 과정을 알아보자.
- 초기 hypothesis function()을 다음과 같이 설정한다.
- Gradient Boosting은 하나의 leaf node에서 시작되므로, 우선 최종 결과를 다음과 같은 과정을 통해 하나로 가정한다.
- 은 loss function이며, 이 hypothesis의 error는 MSE를 따른다고 가정했을 때 식은 다음과 같다.
- loss function의 최소지점을 찾기 위하여 에 대하여 식을 미분한다.
- 이 식을 다음과 같이 다시 쓸 수 있다.
즉, 값의 평균이 곧 모든 sample의 최초의 hypothesis이다.
- 은 loss function이며, 이 hypothesis의 error는 MSE를 따른다고 가정했을 때 식은 다음과 같다.
- 개의 tree에 대하여 :
-
개의 sample에 대하여 residual을 계산한다.
- 이 식을 다음과 같이 다시 쓸 수 있다.
- 이 식을 다음과 같이 다시 쓸 수 있다.
-
만들어진 residual()을 leaf node로 갖는 tree를 생성한다.
(근데 어쩌다 이 된 거지 (원문: Fit a regression tree to the targets giving terminal regions )) -
만약 leaf node로 2개 이상의 residual이 나왔다면 평균을 취한다.
일단 쓰기는 쓰는데 이 단계에 맞는 식인지 모르겠다.
- learning rate 를 반영하여 prediction을 다음과 같이 update한다.
- 이 과정을 반복하여 얻은 값은 이다.
엉엉엉진심뭔소리당가
예제를 통해 알아봅세다.
Gradient Boosting Algorithm example!
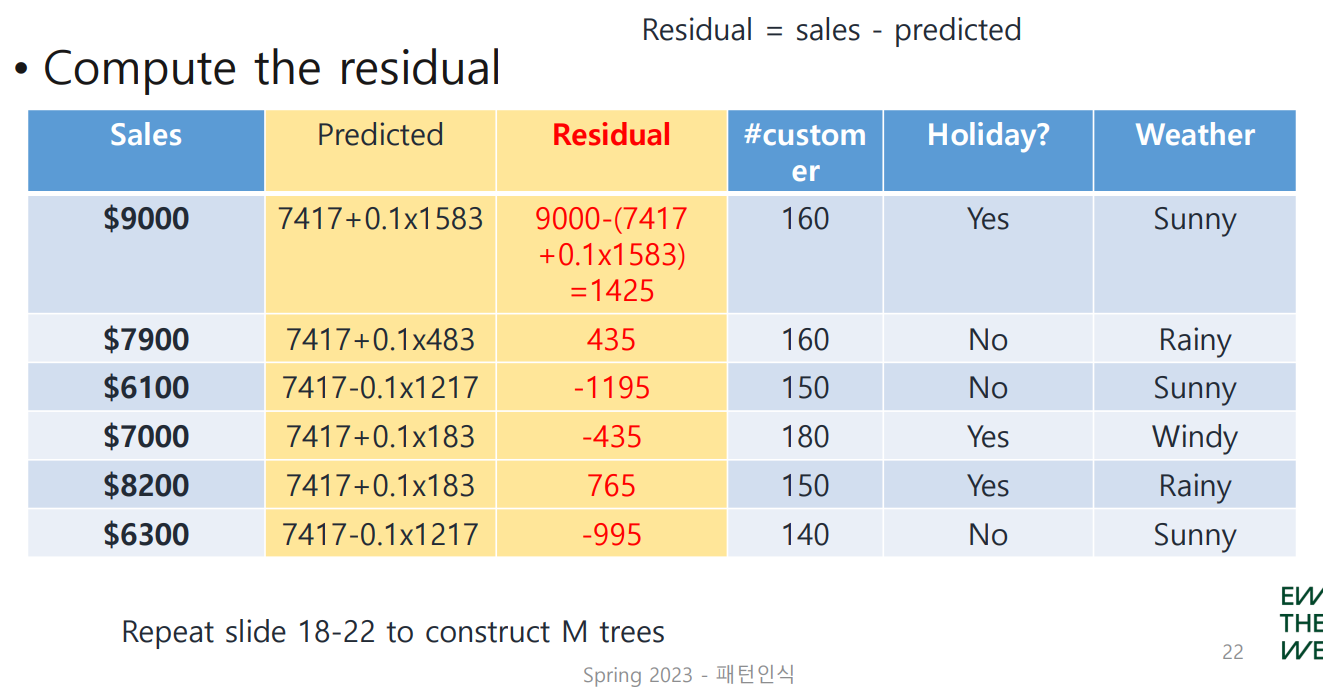
다음 data를 이용해 sales를 예측하는 regression model을 만들어보자.
각 행은 특정 월(月)의 데이터를 나타낸다.
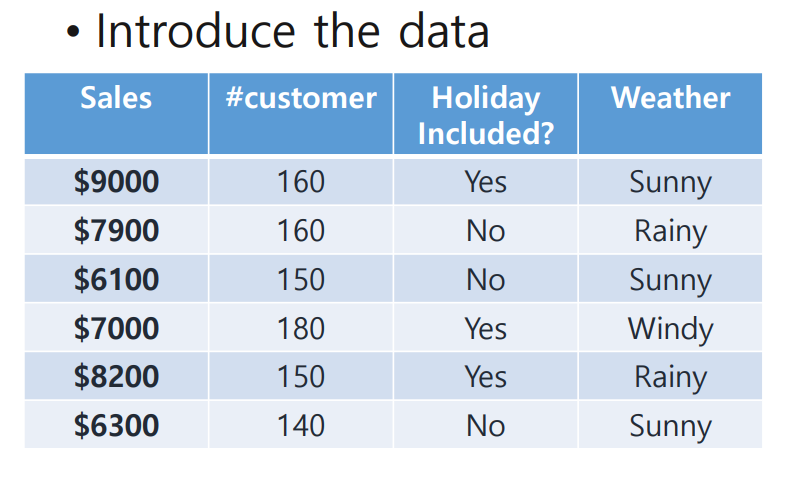
- #customer: 방문객 수
- Holiday Included?: 해당 월에 holiday가 포함되어 있는가?
- Weather: 해당 월에 sunny, windy, rainy 중 어떤 날씨인 날이 가장 많았는가?
sales()의 평균을 구해 초기 hypothesis()로 사용한다.
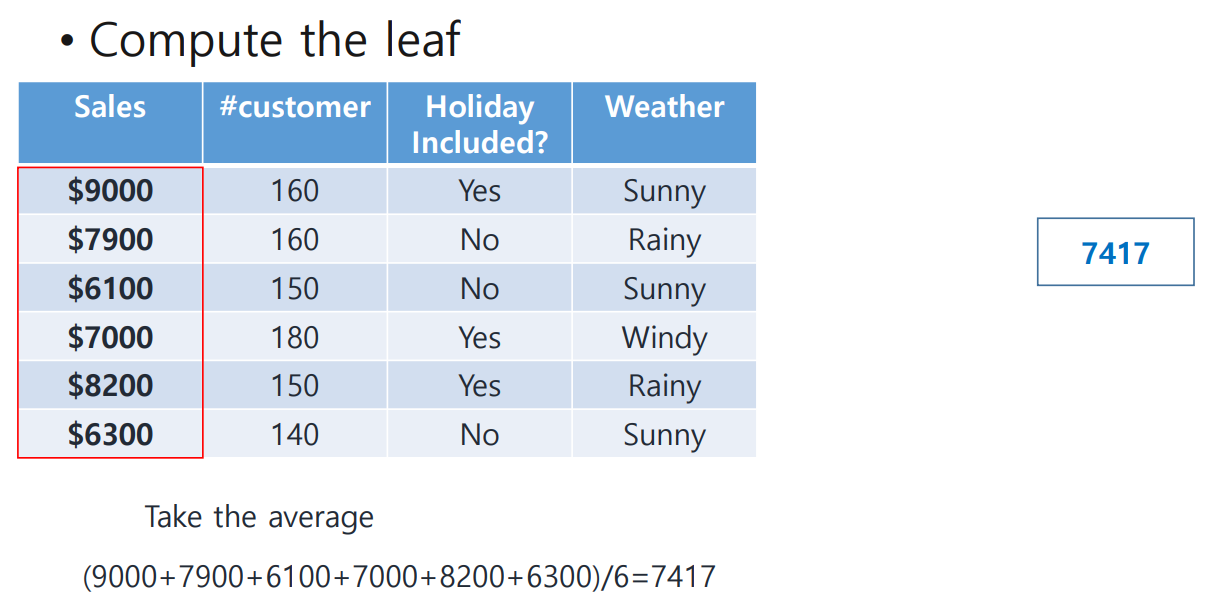
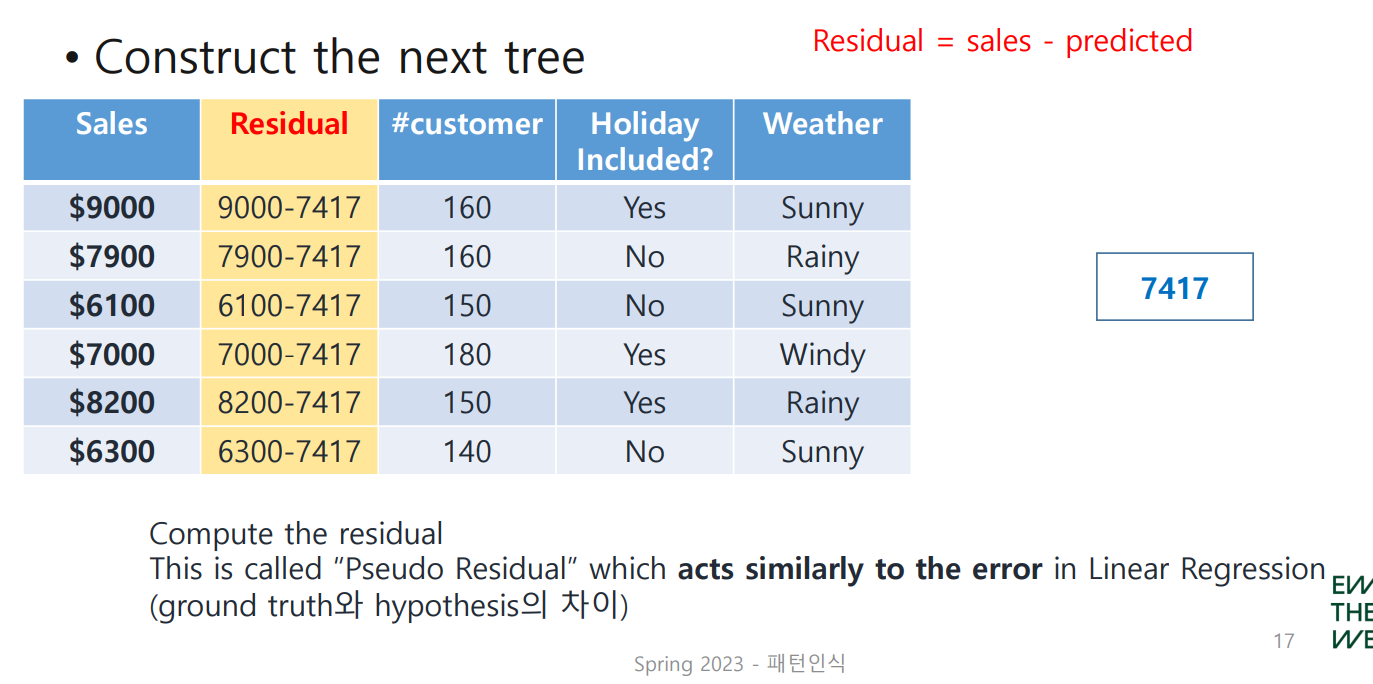
다음 tree를 구축하기 위해 residual을 구하자. 앞서 언급했듯 sales와 hypothesis(또는 predicted, 구체적인 값은 7417)의 차로 이루어지며, 이는 Linear Regression에서의 error와 비슷한 역할을 한다.
residual을 leaf node로 사용하여 만든 tree는 다음과 같다.
설명했듯이 Gradient Boosting은 stump가 아닌 actual tree를 사용하며, 그 대신 leaf node의 수에 제한을 둔다. 이 경우 leaf node의 수를 4개로 제한한 것을 확인할 수 있다!

residual이 2개인 leaf node는 다음과 같이 평균을 취해 넣어준다.
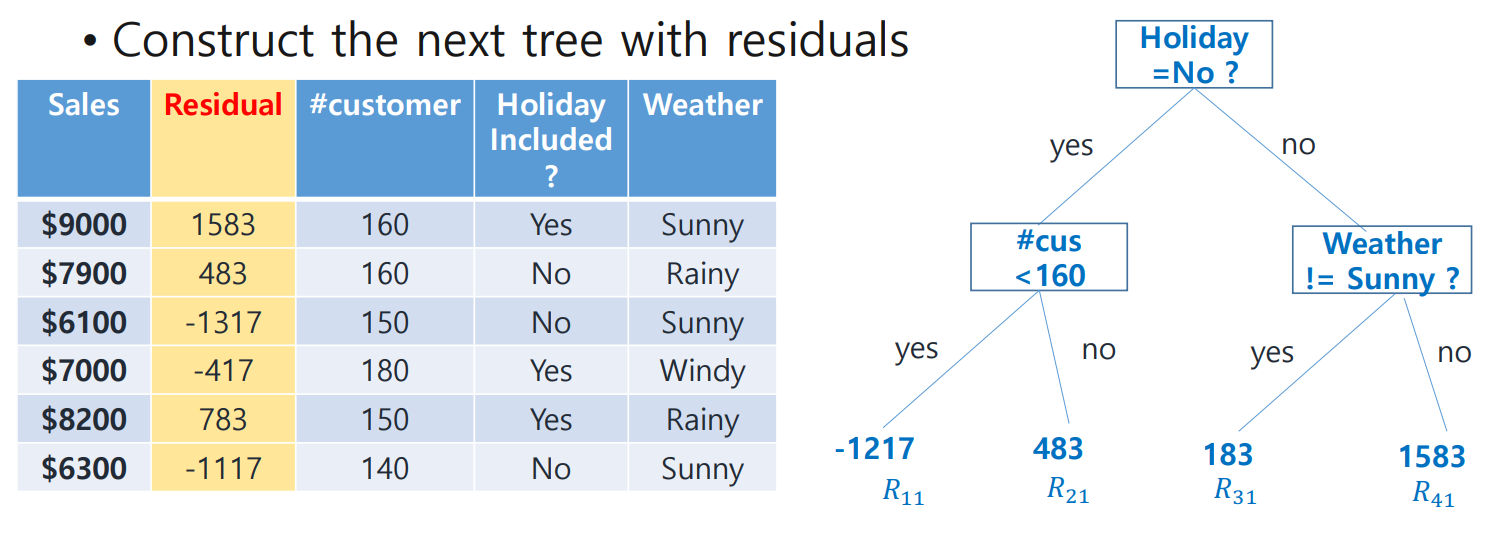
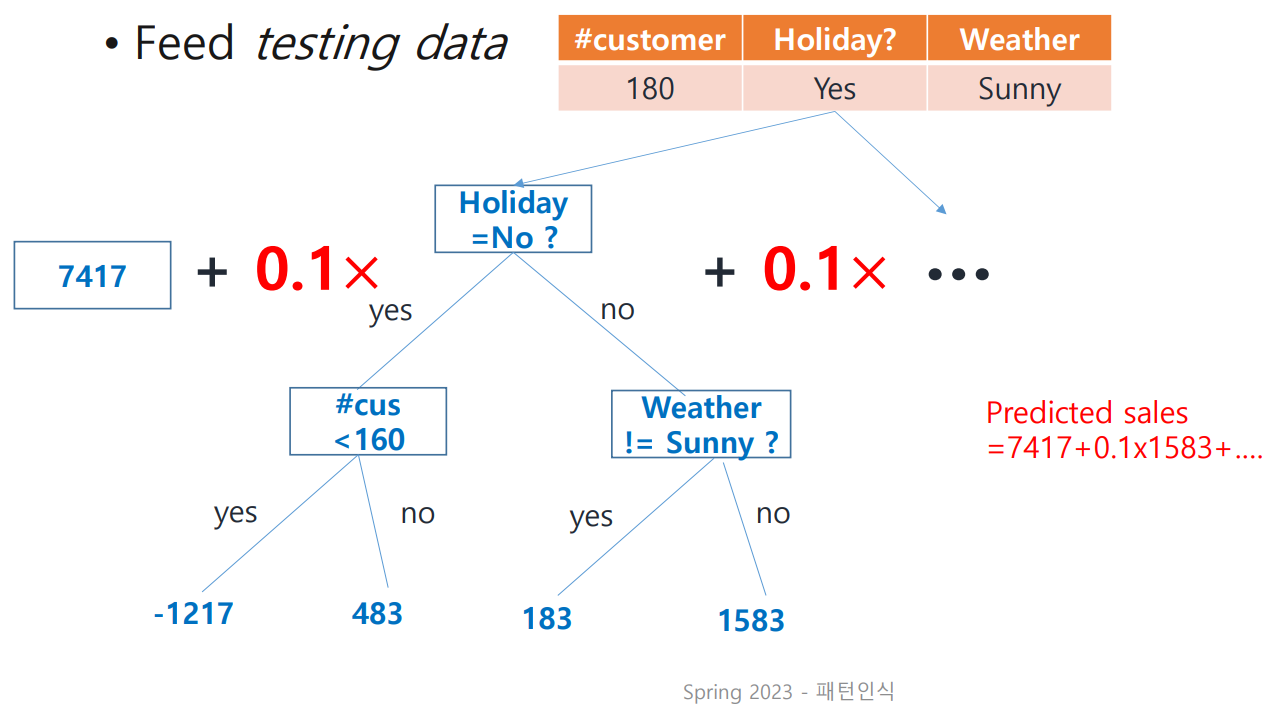
만들어진 tree에 learning rate()를 적용시켜 prediction을 update해 보자.
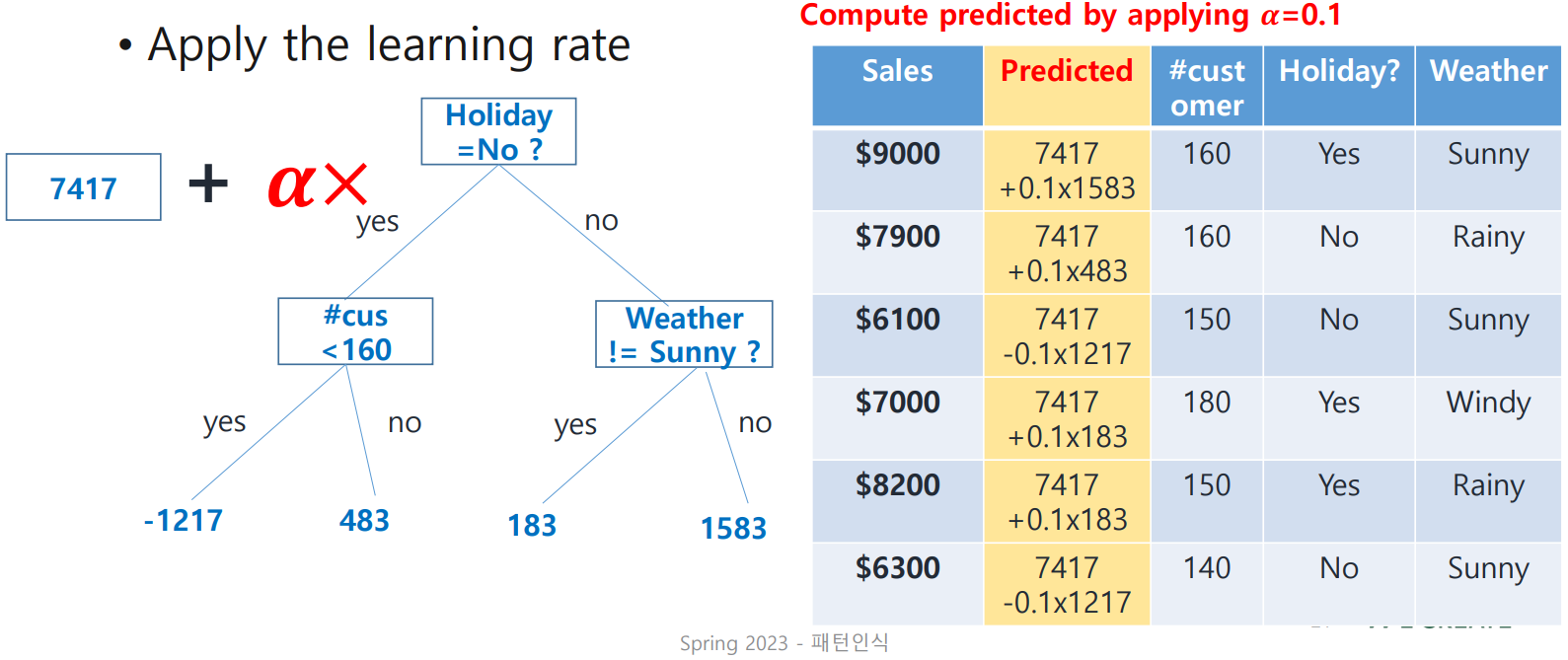
이 과정을 다음과 같이 반복하여 predicted sales를 얻는다!