🐱‍🏍 Likelihood Function

주어진 sample들을 가장 잘 나타내는 distribution을 찾는 방법!

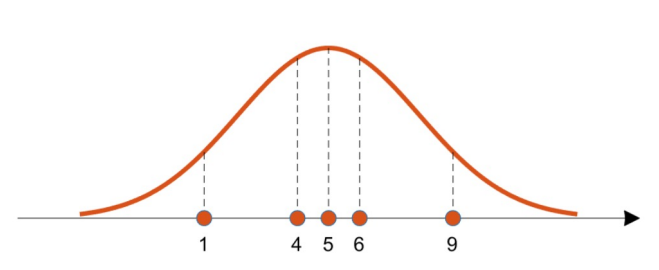
높이는 주어진 sample이 해당 distribution에서 나왔을 확률(Probability)를 의미한다.

Assumptions

• 1, 4, 5, 6, 9 $\sim N(x | μ, σ^2)$
  (평균이 $μ$이고 표준편차가 $σ$인 정규분포를 따른다.)
• 모든 sample은 Independently and Identically Distributed (IID)
  (독립항등분포; 각각의 사건이 독립적이며 같은 분포를 따른다.)

Goal

다음을 최대화시키는 β값을 찾는 것이 목표! (n개의 training sample에 대한 식임)
$∑$가 아니라 $∏$를 쓰는 이유: IID! (각 사건이 독립적)

$p(x|β) = ∏^n_{k=1} \ p(x_k;β)$

교수님이 $p(x|β)$가 아니라 $p(x;β)$가 맞을 것 같다고 하신 건 기억나는데 왠진 잘 모르겟음

🐱‍🚀 Background

✔ Conditional Probability (조건부 확률)

어떤 사건 A가 일어났다는 가정 하에 사건 B의 발생 확률은...

$p(B|A) = \displaystyle \frac {p(A∩B)}{p(A)}$

선형회귀에서는 다음과 같이 쓸 수 있다.

$p(y_i|x_i;β)$
$X$값, 즉 내가 관찰한 데이터가 $y$값, 즉 label이 될 확률밀도를 구하며, $β$값으로 parameterize를 진행한다.

✔ Normal (Gaussian) Distribution (정규분포)

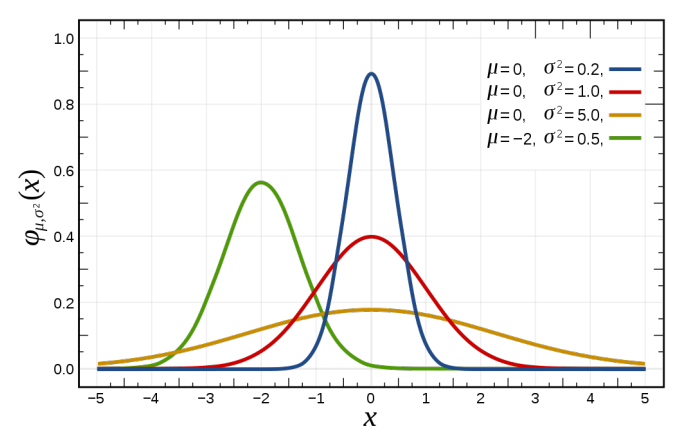
• $μ$는 평균값으로, 위치를 결정한다.
• $σ^2$는 분산으로, 그 값이 작을수록 높이가 커진다.

Probability Density of Normal Distribution

$p(x) = \displaystyle \frac 1 {σ \sqrt {2 \pi}} \exp (- \frac {(x - μ)^2}{2σ^2})$

✔ Maximum Likelihood Estimation

$L(β) = ∏^n_{i=1} \ p(y_i | x_i;β) = ∏^N_{i=1} \displaystyle \frac 1 {σ \sqrt {2 \pi}} \exp (- \frac {(y_i - x^T_iβ)^2}{2σ^2})$

Derivation

여백이 부족하여 적지 않겠다.

1. 대충 Gaussian distribution을 따르는 noise값 $ε$을 hypothesis function에 추가로 더하는 것에서 시작해서
2. 이걸 정규분포 확률밀도식에 대입, $y$와 $X$로 다시 적고
3. likelihood function에서 $p(y_i | x_i;β)$ 대신 넣으면 됨

✔ Log Likelihood Function

If taking log on it...

log를 씌워도 위 값을 최대로 만들어야 함은 동일하기에, likelihood를 최대로 만들기 위해서는 $∑^N_{i=1}(y_i - x^T_iβ)^2$, 즉 error function이 최소가 되어야 함!

근데 $y_i - x^T_iβ$가 어쩌다 $y_i - β^Tx_i$가 되는 거지

🐱‍🏍 Bias and Variance

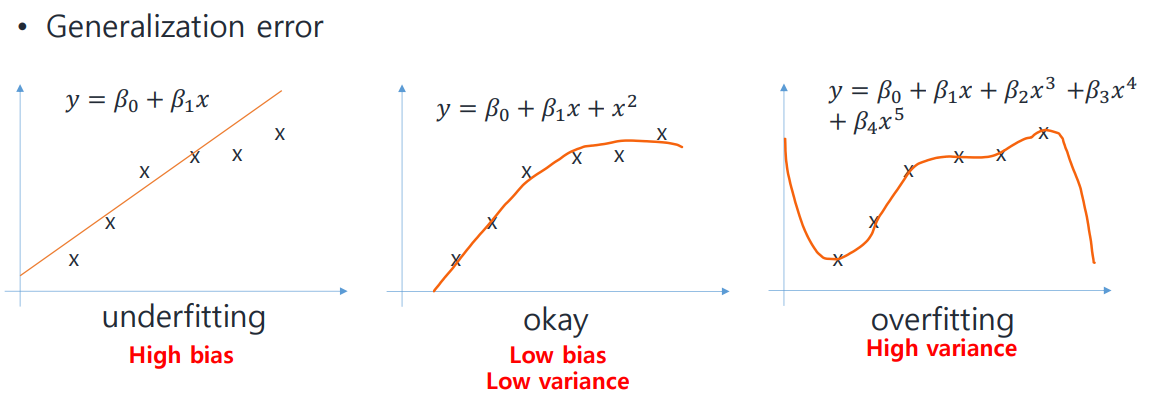
✔ Bias (편향)

Difference between the average prediction and the truth value
참값으로부터 멀리 떨어져 있을수록 크다.

✔ Variance (분산)

Variability of prediction for a data point
각 값이 서로 멀리 떨어져 있을수록 크다.

Bulls-eye Diagram

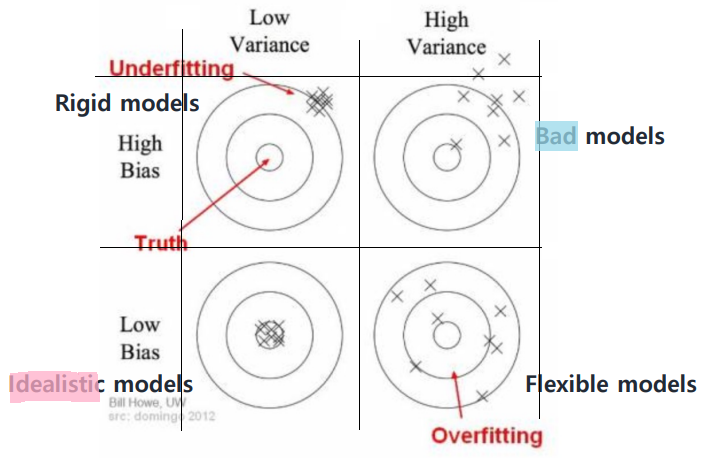
• flexible: 변동성이 크다는 것! (Overfitting의 단점)
  적용하는 데이터를 달리할 때마다 예측값이 크게 달라짐.
• rigid: 뭐라 번역해야 하지 암튼 (Underfitting의 단점)
  무슨 데이터에 적용시키든 참값에서 떨어진 유사한 값만 나옴.

✔ Minimize the Total Error

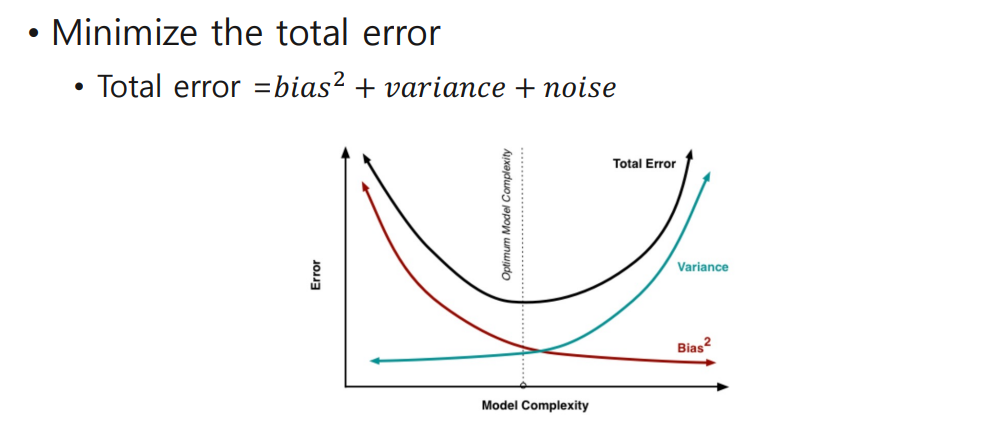
근데 이건 가볍게만 얘기하고 넘어가심
근데 어케 내실지 모름 내신같이 나온다고 들어서 ......

Solution for Underfitting & Overfitting

Underfitting의 경우 training sample 수가 너무 적어서 발생하는 게 대다수고, parameter를 추가하는 것으로 대부분 해결됨.
하지만 Overfitting은...

• Reduce the model complexity
  이 경우 underfitting이 다시 발생할지도...
• 가장 좋은 것은 Regularization! (정규화)
  
  

아래 내용 너무 마음이 힘들다...

🐱‍🚀 Background

✔ L1 & L2 Norm

두 벡터 간의 거리를 측정하는 두 가지 방법!

L1 Norm (Manhattan Distance)

$||x||_1 = \displaystyle \sum^n_{i=1}|x_i|$

ex) $x = [1, 2, 3], \ ||x||_1 = |1|+|2|+|3|$

L2 Norm (Euclidean Distance)

$||x||_2 = \displaystyle \sqrt {\sum^n_{i=1}|x_i|^2}$

ex) $x = [1, 2, 3], \ ||x||_2 = \sqrt {|1|^2+|2|^2+|3|^2}$

🐱‍🏍 Ridge and Lasso Regularizations

✔ Ridge Regression

L2 Regularization! (i.e., $||β||_2 = \sqrt {\sum_iβ^2_i}$)

$J(β) = \sum^N_{i=1}(y_i-β_0-\sum^p_{j=1}X_{ij}β_j)^2$
$\argmin_β\sum^N_{i=1}(y_i-β_0-\sum^p_{j=1}X_{ij}β_j)^2 + λ\sum^p_{j=0}β^2_j$
subject to $\sum^p_{j=0}β^2_j\leq c$ (some constant $c$)

파라미터(β)의 제곱에 비례하는 페널티 항 람다를 추가하여

• 파라미터값이 크면 더 큰 영향을 미치도록!
• 작다면 반대로!

행렬 형태로 쓰면 다음과 같다.

$J(β) = (y-Xβ)^T(y-Xβ)+λβ^Tβ$
$β=(X^TX+λ)^{-1}X^Ty$ (by normal equations)

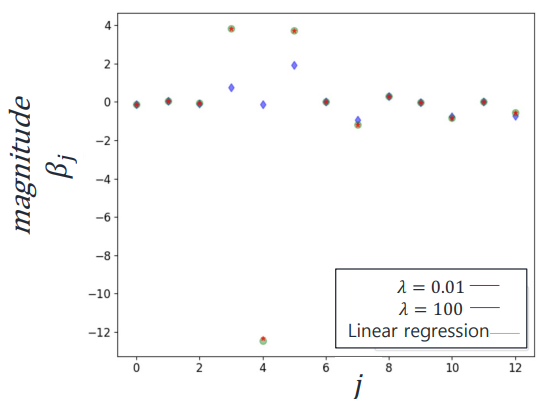
람다값이 클수록, 파라미터의 제곱의 값이 클수록 큰 폭으로 정규화되는 것을 확인할 수 있음. ($λ=100$인 파란 점)

✔ Lasso Regression

L1 Regularization! (i.e., $||β||_1 = \sum_i|β_i|$)

얘는 파라미터(β)의 절댓값에 비례하는 페널티 항 람다를 추가!
Ridge~와는 다르게 Feature Selection 효과를 가짐.
(무의미하다고 여겨지는 feature는 아예 $0$으로 만들어 버리는 것!)

$J(β) = \sum^N_{i=1}(y_i-β_0-\sum^p_{j=1}X_{ij}β_j)^2$

$\argmin_β\sum^N_{i=1}(y_i-β_0-\sum^p_{j=1}X_{ij}β_j)^2 + λ\sum^p_{j=0}|β_j|$

subject to $\sum^p_{j=0}|β_j|\leq c$ (some constant $c$)

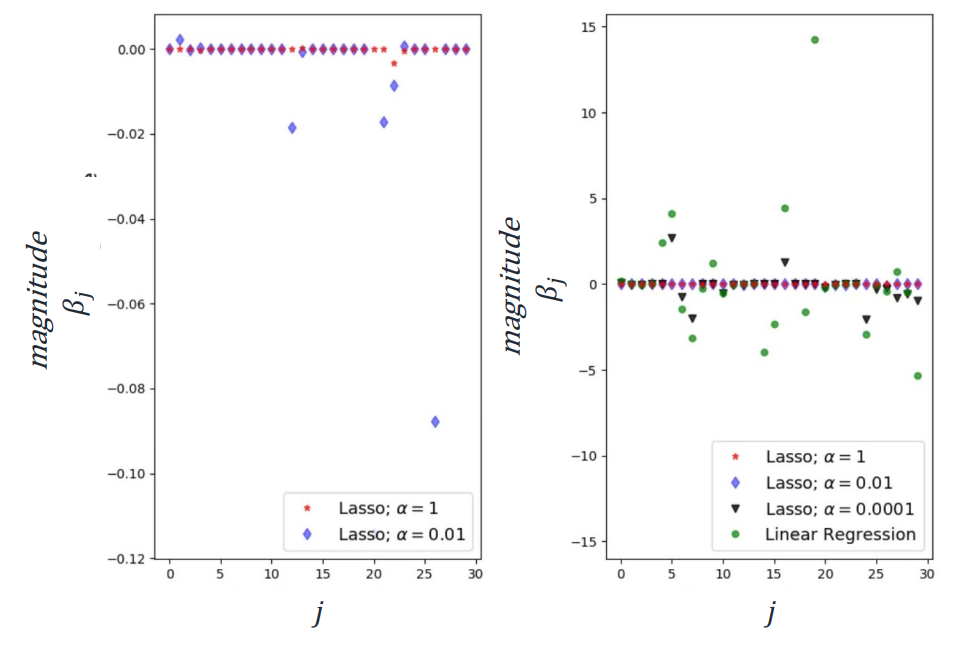
대부분의 feature가 $0$이 되어버린 것을 확인할 수 있음.

contour plot으로 알아보기

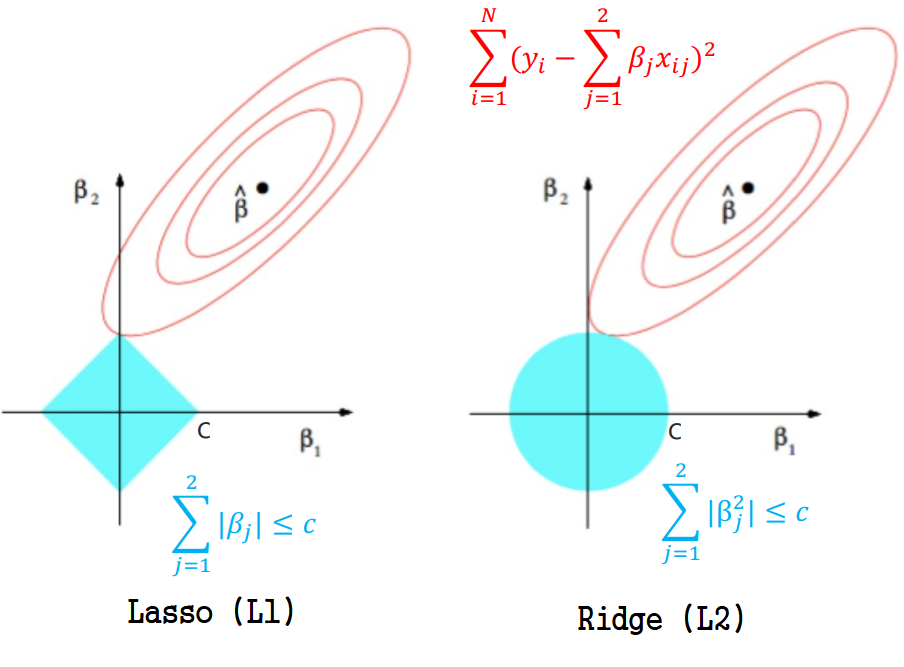
• Elliptical contours(타원형 곡선): cost function
• Diamond, circle plots: constraint regions(제한 영역?)
• $\hat{β}$: error값이 최소가 되는 지점

What if the constraint region gets bigger?

$c$가 커질수록 constraint region가 넓어지며, 이것이 contour과 교차되는 지점/영역이 곧 정규화를 통해 결정한 고려할 영역! 이라고 이해했음.

What if the region hits $\hat{β}$?

$c$가 $\hat{β}$까지 도달하도록 증가시키면 overfitting 확률이 커지며 regularization의 의미가 없어짐?

Ridge와 Lasso 부분을 작성하지 못했다...

---

참고자료

• https://ebbnflow.tistory.com/330
• https://towardsdatascience.com/bias-variance-and-how-they-are-related-to-underfitting-overfitting-4809aed98b79