모델의 성능을 어떻게 평가할 수 있을까?
- Bias-variance tradeoff
- Data splits
- Cross validation
- Classification metrics
- Regression metrics
Bias-variance Tradeoff 복습
Example
주어진 data에 맞는 hypothesis function으로,
이차함수 가 다음과 같이 제시되었다고 하자.
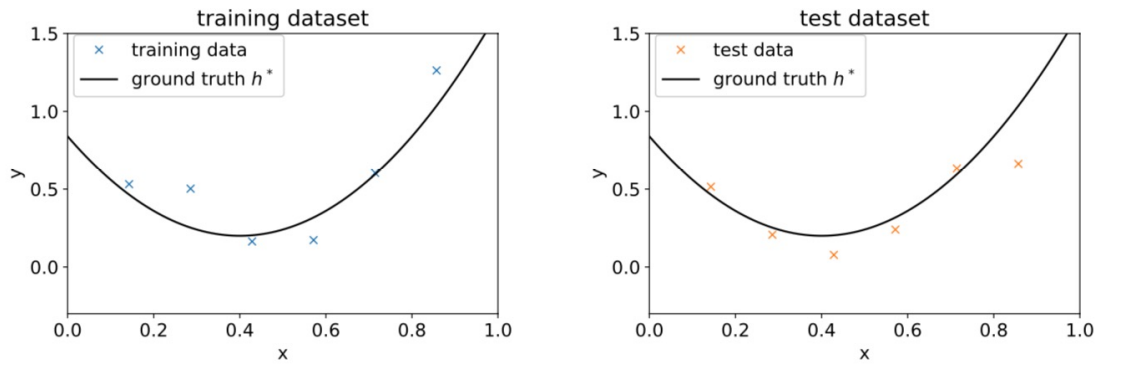
이며, 오차로 표현한 식은 이다.
모델의 학습은 를 줄이는 방향으로 진행된다.
같은 data의 hypothesis로 linear function을 제시한 경우에는 어떨까?
Underfitting!
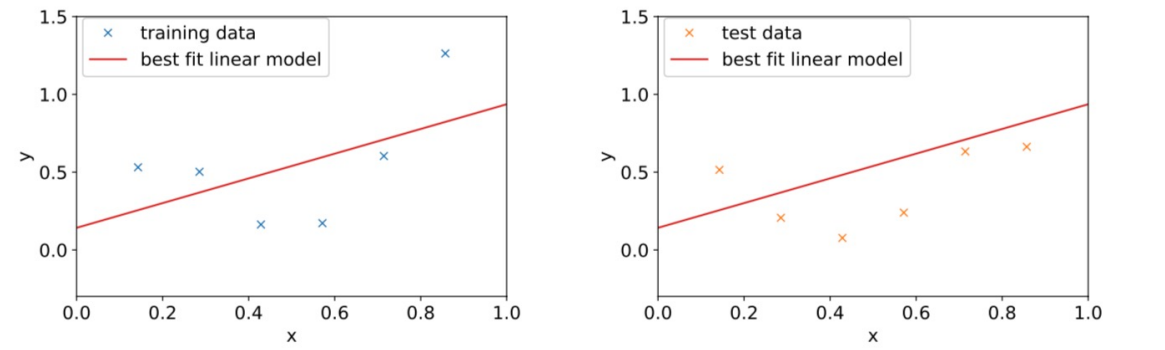
underfitting(high bias)인 것을 확인할 수 있다.
이를 해결하고자 데이터 샘플을 추가하거나 노이즈를 제거한 모습은 다음과 같다.
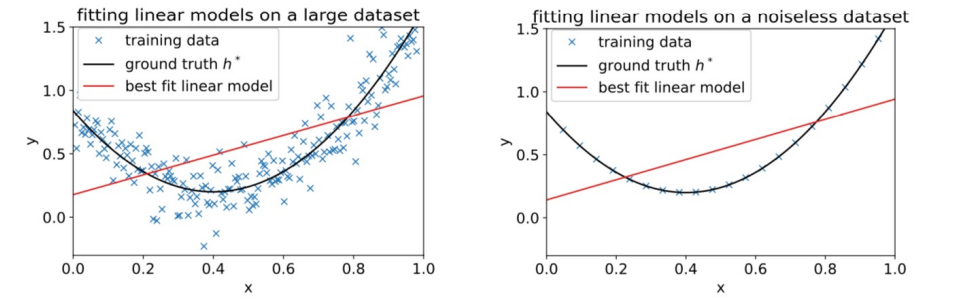
그다지 도움이 되지 않는 것을 확인할 수 있다.
data 자체가 linear하지 않고 이차함수 형태를 띠고 있으므로 linear function으로는 그 구조를 정확히 표현할 수 없는 것이다.
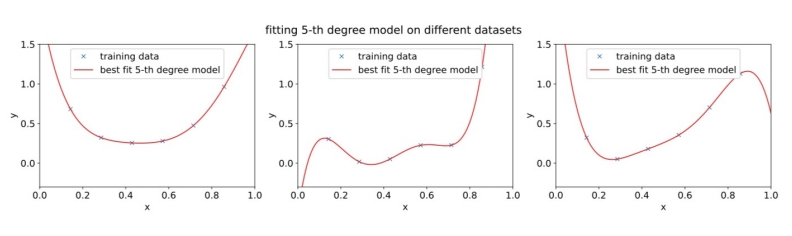
이번에는 같은 data의 hypothesis로 5차함수를 제시한 모습을 살펴보자. (feature 개수를 늘린 것)
Overfitting!
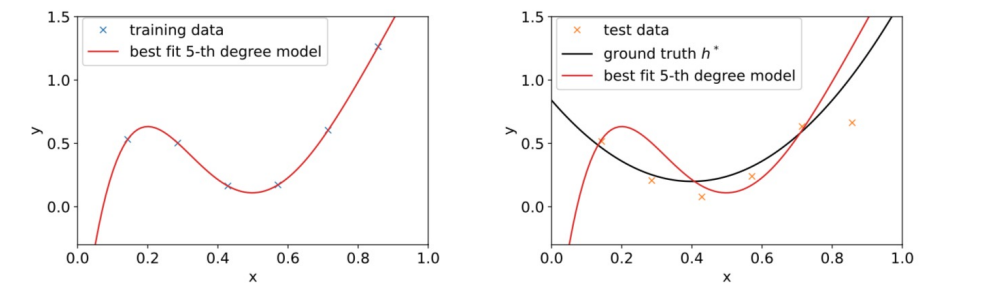
overfitting(high variance)인 것을 확인할 수 있다.
training data에는 완전히 fit하지만, testing data에는 하나도 들어맞지 않는 것을 볼 수 있다.
high bias? high variance?
high bias는 단순히 hypothesis function이 training data에 fit하지 않은 상태를 이른다고 보면 될 듯
high variance는, 같은 distribution을 따르는 data 내에서 뽑은 서로 다른 training set들로 여러 model을 구축했을 때, 이 model들 간의 variance의 양이 큰 것
Bias-variance Tradeoff
모든 경우 반드시 일어난다 << 는 아님!
영어 원문 표현에는 may가 들어갔다는 사실을 숙지하길.
- If the model is too "simple" and has very few parameters?
⇒ large bias but small variance, underfitting - If the model is too "complex" and has very many parameters?
⇒ large variance but small bias, overfitting
Bias-variance Tradeoff for Regression
- dataset:
- hypothesis:
단, 오차 ξ는 평균이 0, 분산이 인 normal distribution을 따른다. ()
- dataset 로 구축한 model의 식을 로 표현한다.
- 임의의 sample 을 뽑아 hypothesis를 test한다.
(, 즉 는 오차 를 갖는 test data)
이때의 test error의 기댓값을 다음과 같이 구한다.
MSE() =
기댓값?
확률적 사건에 대한 평균값으로, 사건이 일어나서 얻는 값과 그 사건이 일어날 확률을 곱한 것을 모든 사건에 대해 합한 값이다. 이것은 어떤 확률적 사건에 대한 평균의 의미를 갖는다.
대충 평균치라고 이해하자!
통계를 배우고 더 생각을...
🐱👓 중요!
아래의 식 도출 과정보다는 맨 마지막 식에 집중!

MSE
-
: 추정치. (hypothesis를 대표하는 값) testing data를 적용시켜, 모델의 성능을 나타내는 값이다.
-
: 위 설명 그대로! 간단히 보면 ground truth를 나타낸다고 할 수 있다. (best possible model, 주어진 dataset 를 가장 잘 나타냄)
-
: 하나의 한정된 dataset 로 학습시킨 모델 그 자체를 나타내는 값이다.
bias^2
데이터에 기인한 문제가 아닌,
모델 자체의 성능(approximation)의 문제
variance
학습데이터의 유한함과 그 유한한 정보로 학습한 모델의 성능이
특정 데이터에만 잘 동작하게 제한됨

결과적으로 bias와 variance 간의 tradeoff가 잘 이루어지는 모델을 선택해야 하며, 해당 내용을 그래프로 나타내면 아래와 같다.

부가적으로 설명하자면 모델의 복잡도가 높아질수록 training set에 대한 이해도가 높아지며, 이에 따라 training data의 noise까지 반영하여 문제가 될 수 있다.
Dataset Split
Train / Validation / Test set
과적합을 방지하기 위해 training set와 testing set을 달리해야 하며, validation set을 만드는 것도 도움이 된다.
Validation Set
validation set은 training set을 쪼개어 만들며, 학습 도중에 진행되는 아래와 같은 과정에서 training set만 사용할 경우 overfitting의 가능성이 높아지므로 이를 방지하기 위해 만들어 사용하게 된다. (이때 testing data는 테스팅 시점이 아니라면 절대 건드려서는 안 됨)
- Model Selection
- Hyperparameter Tuning
- Early Stopping
Steps for Model Assessment
- dataset을 training, validation, testing set으로 split한다. (각각 )
- 을 이용해 모델을 학습시킨다.
- 을 이용해 가장 작은 을 갖는 best model을 선택한다.
- 를 이용해 3에서 선택한 모델을 평가한다.
위와 같이 data를 랜덤하게 섞어 미리 train, validation, test로 나눈 뒤 학습을 진행하는 것은 Hold-out Cross Validation이다. (보통 training set의 비율이 가장 큼! 교수님은 60퍼 20퍼 20퍼로 예를 들어주심)
데이터셋이 작은 경우?
size() hundreds, 즉 몇백 개 정도!
이런 경우 위와 같이 split하면 데이터의 양이 너무 적어질 수 있다. 이럴 땐 다음과 같은 validation 방안을 적용할 수 있다.
K-fold Cross Validation

dataset을 개로 split한 뒤, 매 iteration마다 하나를 testing set으로 사용하여 개의 결괏값에 대하여 평균을 취한다. (위 경우 )
pseudo code로 알아보자.

-
dataset 를 랜덤하게 split하여 서로 겹치지 않는(disjoint) subset 개를 만든다. ()
-
여러 개의 모델 에 대하여 다음과 같이 평가한다:
for
- Train: testing set으로 사용할 를 제외한 나머지 subset을 모두 합쳐 모델 에 학습시키고, 이로부터 hypothesis 를 얻는다.
- Test: testing set 에 대해 hypothesis 로 평가하여 , 즉 error값을 얻는다.
이렇게 얻은 개의 error값에 평균을 취하여, 모델 의 estimated generalization error를 얻는다.
-
여러 개의 모델 에 대하여 estimated generalization error가 가장 작은 것을 선택하고, 전체 training set 으로 다시 학습시켜 최종 hypothesis를 구한다.
🥗 validation을 다 끝내고 얻은 최종 모델에 대하여 test는 안 하는 건가?
데이터셋이 더!! 작은 경우?!
size() < 100, 즉 백 개 이하!
이럴 땐 또 다른 validation 방안을 적용할 수 있다.
Leave-one-out Cross Validation

값을 따로 지정하는 것이 아니라, 전체 data 개수로 아예 split해버리는 것! 개만큼의 subset이 생기며, k-fold와 마찬가지로 하나씩 testing set으로 사용하고 결괏값의 평균을 구하게 된다.
모델의 성능을 판단하는 여러 지표에 관해 알아보자. 우선 분류에 적용할 수 있는 지표는 무엇이 있을까?
Classification metrics
TP, TN, FP, FN
아래 4개의 값을 이용하여 여러 성능 지표를 계산하게 된다.
-
True Positives
관측값이 class에 속할 것으로 예상 & 실제로 속함 -
True Negatives
관측값이 class에 속하지 않을 것으로 예상 & 실제로 속하지 않음 -
False Positives
관측값이 class에 속할 것으로 예상 & 실제로는 속하지 않음 -
False Negatives
관측값이 class에 속하지 않을 것으로 예상 & 실제로는 속함
당연한 사실이지만 모델이 바르게 판단한 것, 즉 TP, TN이 많을수록 좋다.
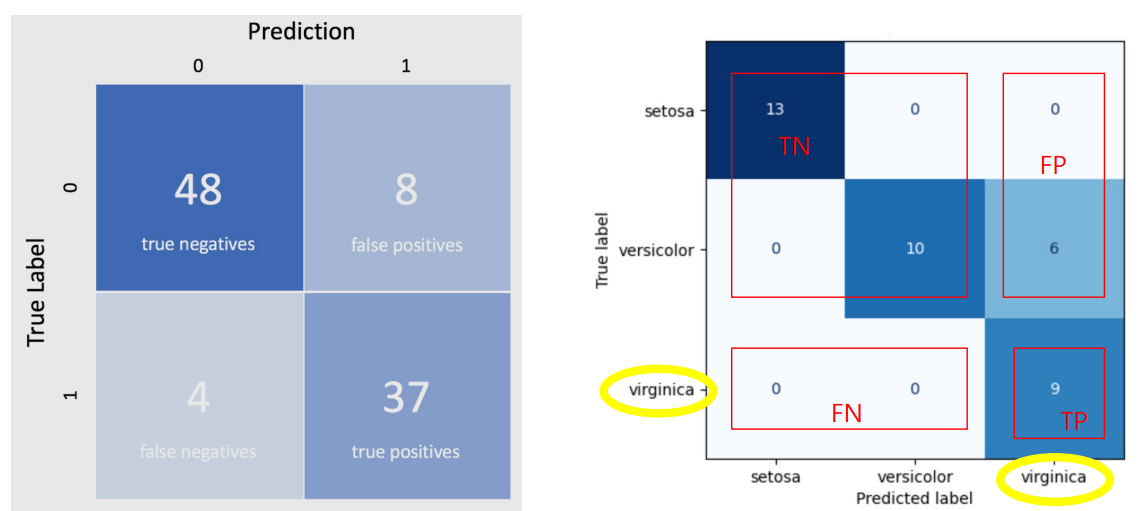
이 비율을 시각화해서 볼 수 있도록 하는 것이 아래의 confusion matrix!
Confusion Matrix
pos:1, neg:0
기타 metrics에 대해서도 알아보자.
Accuracy
Accuracy =
dataset이 imbalanced한 경우, 즉 특정 class의 sample만 굉장히 많거나 적은 경우 accuracy를 신뢰하기 힘듦.
accuracy가 높다고 무조건 좋은 모델이라고 판단할 수는 없다는 것! 이런 경우 이용할 수 있는 다른 지표는 무엇이 있을까?
Precision
When we want to be very sure about our prediction
Precision =
positive로 판단한 경우 중 맞는 것(True)의 비율을 나타낸다.
학습시킨 모델의 예측값에 대해 확신을 갖고 싶을 때 이용!
Recall
When we want to capture as many positives as possibles
Recall (True Positive Rate) =
모델의 예측값과 상관없이 실제 positive인 sample 중 correct하게 판단된 것(True Positive)의 비율을 나타낸다.
내가 관심 있는 클래스를 맞게 판단하는 것에 치중을 둘 때, 최대한 많은 positive를 고려하고자 할 때 이용!
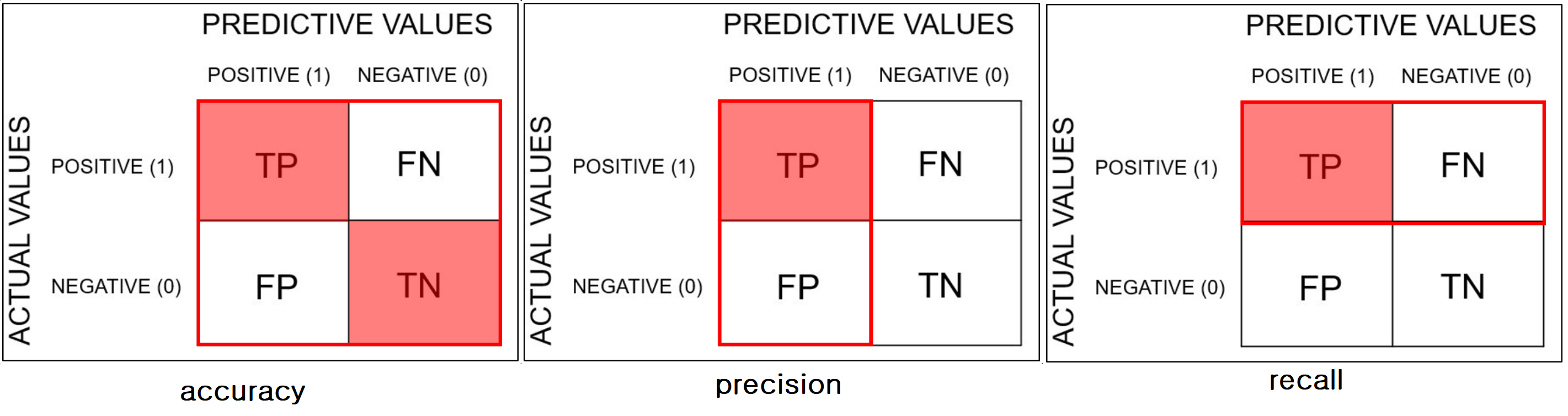
정리하자면 이와 같다!
위 사진은 교수님 PPT와는 pos, neg 순서가 반대로 되어 있는 것에 주의.
Threshold
label을 할당하기 전, 분류 모델은 에서 사이의 probability값을 반환한다!
이에 대한 기준을 정해 label을 어떻게 할당할지 정하기 위해 threshold를 정해줘야 하는 것.
구한 proba가...
- threshold 이상일 경우 pos로 분류
- 반대의 경우 neg로 분류
threshold가...
- 에 가까워질수록 더 많은 sample을 pos로 분류
- 에 가까워질수록 더 적은 sample을 pos로 분류
예제를 통해 알아보자.
e.g.
아래 경우를 보고 precision, recall을 직접 계산해 보자.
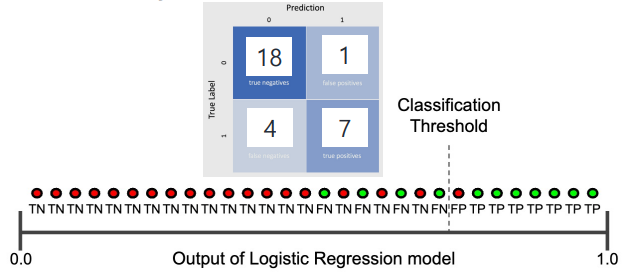
- precision:
- recall:
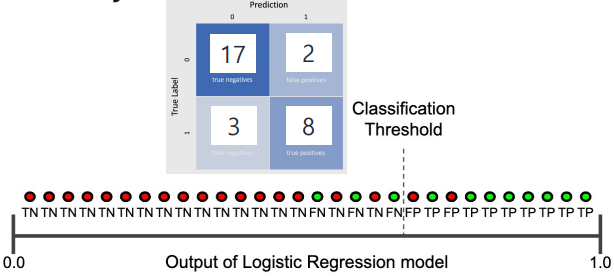
- precision: (decreased)
- recall: (increased!)
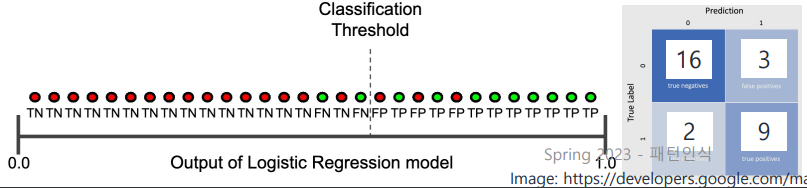
- precision: (decreased)
- recall: (increased!)
정리하자면 다음과 같다!

즉 threshold를 감소시킬수록 positive로 예측하는 sample도 많아지므로 precision이 감소하는 것!
교수님 우째서 아니 빨강이 보통 증가 아닌가 아님 말고
어느 metrics를 중요하게 보느냐에 따라 초점을 맞추는 부분이 달라지겠지만, 일반적으로는 precision과 recall의 균형을 맞추게 된다!
둘 모두를 고려하기 위해서는 다음과 같은 방안을 고려할 수 있다.
F1-score
precision과 recall 모두 좋은, 즉 둘 모두를 고려하여 균형을 맞춘 모델을 원할 경우 사용할 수 있는 지표이다.
(precision을 증가시켜도, recall을 증가시켜도 f1 score는 증가함)
그래프 해석하기!
아래 그래프는 class에 대한 sample의 분포가 매우 불균형한 dataset을 나타낸다.
(negative sample은 개인 반면 positive는 개밖에 되지 않는 경우)

Q1. recall과 precision을 나타내는 부분은 각각 어디일까?
- Recall: (bar 위 주황 점)/(전체 주황 점)
- Precision: (bar 위 주황 점)/(bar 위 전체 점)
Q2. bar를 위로 옮긴다면!? (위 그림에서 하늘→분홍)
threshold가 높아진다는 뜻이며, 이에 따라...
- Recall: decreased
- Precision: increased!!
특히 precision은 threshold가 계속해서 증가해 에 가까워질 경우, positive로 판단하는 sample 수가 에 가까워지므로 infinite로 나아간다...
★ Q3. 불균형한(imbalanced) dataset에는 어떤 지표가 가장 좋을까?
둘 중에는 precision!
(positive sample만 고려하는 recall에 비해, FP를 다룸으로써 현재 큰 비율을 차지하는 negative sample의 영향을 고려할 수 있음)
Precision depends on how rare the positive class is. Thus, it is used when positive class is more interesting than the negative class.
Q4. bar가 매우 아래쪽에 위치한다면, (threshold = ) precision이 가리키는 것은 무엇일까?
결과적으로 모든 sample을 positive로 판단하게 되므로, 전체 sample 중 TP의 비율, 즉 그냥 positive sample의 ratio(base rate)가 된다!
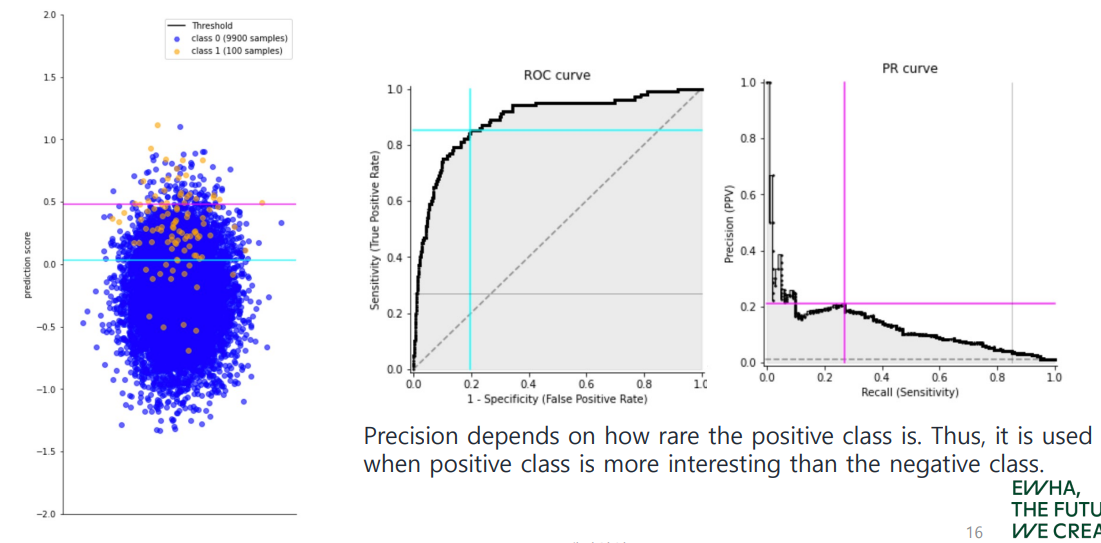
ROC Curve
x축은 FPR, y축은 TPR이다.
- FPR = , 즉 전체 negative sample 중 positive로 잘못 분류한 것의 비율이다.
- TPR: Recall!
PR Curve
x축은 Recall, y축은 Precision이다.
기말 paper 만들며 다시 정리해 보자!!
Regression Metrics
보통 MSE(Mean Squared Error)를 많이 사용한다. (predicted output과 관측값 사이의 차이를 제곱한 것의 평균)
