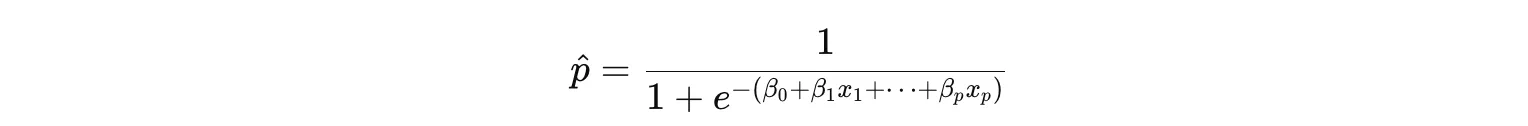1. 학습 키워드

• 로지스틱 회귀
• 오즈
• 혼동행렬

2. 학습 내용

1) 분류

미리 정의된 범주(label) 중 하나로 분류하는 문제

통계학: 어떤 요인이 결과를 설명하는가?
머신러닝: 정답을 얼마나 잘 맞추는가?
→ 조건부 확률을 모델링하는 개념은 동일함.

분류 - 선형회귀의 한계

선형 회귀는 직선으로만 설명하려고 함. 그렇기에 분류 문제의 비선형적 특성을 반영하지 못한다.

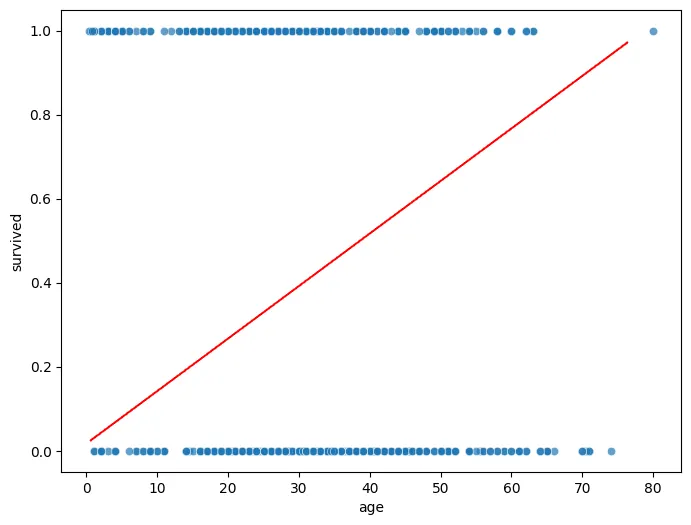
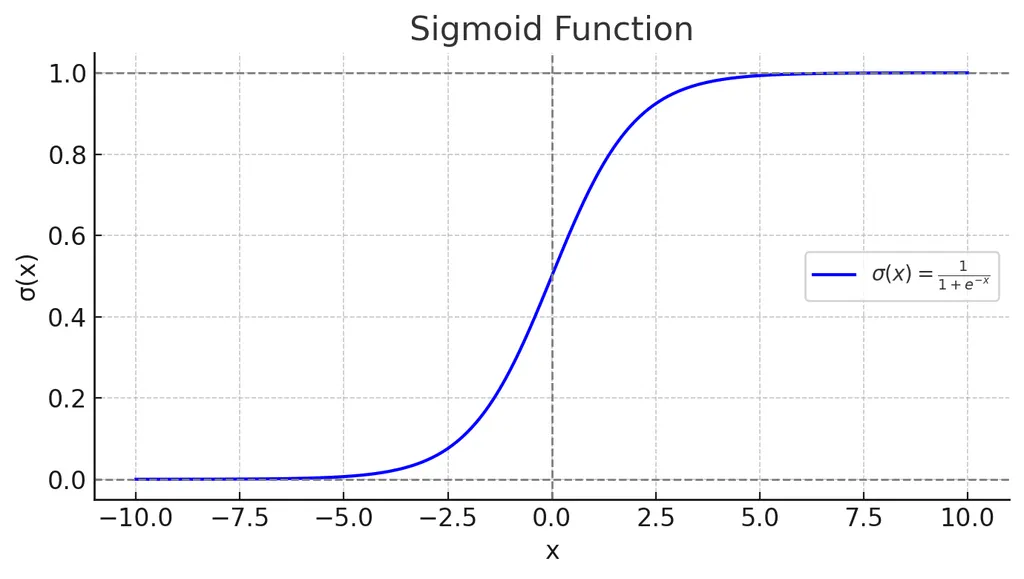
따라서 시그모이드 함수를 바탕으로 0~1 확률을 자연스럽게 만드는 로지스틱 회귀 사용이 필요함.

2) 로지스틱 회귀

로지스틱 회귀는 X가 증가하면 성공 가능성이 몇배나 증가하는지 설명하는 모델로 해당 사건이 발생할 확률을 예측하는 분류 모델이다.

• 확률을 X에 따라 모델링을 하고싶다는 생각에서부터 시작이됨.
• 회귀(=선형) 모델이기 때문에 y = β0 + β1x1 + β2x2 + ...의 형태를 따른다.
• y의 값을 확률로만 나타내면 0~1 사이로 범위가 제한되어 변화가 작으며 선형식에 넣기에 한계가 있음.
• 확률 → 오즈 → 로짓오즈(로그오즈)를 사용했으며 선형식 구현을 위해 최종적으로 로짓오즈를 사용함.

로지스틱 회귀의 핵심개념: 오즈와 오즈비

확률은 ‘얼마나 자주 성공하냐’, 오즈는 ‘성공이 실패보다 몇 배 더 많은가’를 나타냄

개념	의미	예시 (p=0.8)
확률(p)	전체 중에서 얼마나 성공하는가?	80% 성공
오즈(odds)	성공이 실패보다 몇 배 많은가?	0.8 / 0.2 = 4 (4:1)
	- 성공:실패 비율 = p / (1-p)

오즈비: 두 그룹의 오즈를 비교한 값

모델의 결과를 해석할 때 사용하는 지표임(exp(β))

• 남성 구매 확률 = 0.8 → 오즈 = 4
• 여성 구매 확률 = 0.4 → 오즈 = 0.667
• 오즈비 = 4 / 0.667 ≈ 6

→ 남성의 구매 오즈가 여성보다 6배 높다!

왜 확률로 비교하지 않고 오즈비로 비교할까?

• 확률로 보면 변화가 작아 보이지만, 실제 성공 가능성은 훨씬 크게 차이가 나기 때문이다.

로짓함수

오즈에 로그를 씌운 형태(로그 오즈)

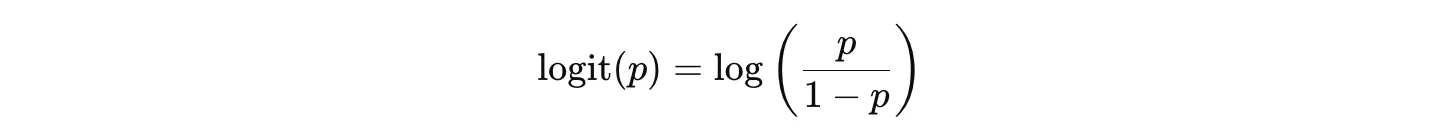
🔥 왜 오즈를 그대로 쓰지 않고 로그를 씌울까?

1) 오즈는 곱셈적 특징을 가지기 때문에 선형적 관계를 이루지 않는다.

• 오즈값은 0 ~ ∞의 범위이므로 그대로 선형회귀식과 결합하기 어렵다. 선형 회귀식을 만들어야 하는데 y의 값을 오즈로 사용하면 -∞부터 ∞가 아니라 0부터 ∞로 제한되기 때문이다.
• 예시를 들면 β0 = 0.2, β1=0.1인 상황에서 x=-5이면 음수가 되어서 오즈로 해석할수가 없음.
• 오즈는 곱셈적 특징을 가지고 있어 X의 변화에 따라 y값이 선형적으로 증가하는 것이 아니라 매우 큰 변화로 이어질 수 있다.

2) 오즈에 로그를 취하면 덧셈적·선형적 구조로 바뀐다.

• 덧셈적이란? X가 1 증가하면 y값은 β1가 일정하게 증가하는 것.
• 비대칭 구조 -> 대칭 구조
• 오즈에 로그를 취하면 -∞ < log(odds) < ∞ 범위라 회귀식에 넣기 적합해짐

3) 해석이 쉬워짐

• 로그 오즈는 숫자가 일정한 폭으로 변하기 때문에 변수의 영향이 더 예측 가능하고 해석하기 쉬운 형태가 됨

확률(p)은 언제나 0과 1 사이에 제한되지만, logit(p)는 –∞부터 +∞까지 아무 값이나 가능하다.
→ 제한 없는 값 범위를 가지므로, 직선 형태의 회귀식(선형식)으로 모델링하기에 적합하다.

로지스틱 회귀란

로지스틱 회귀는 확률을 예측하고, 오즈비를 통해 X가 증가하면 성공 가능성이 몇 배로 변하는지를 설명하는 모델

• 로지스틱 회귀식
  $\log\left(\frac{p}{1 - p}\right) = \beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p$
• p = y가 1일 확률
• 1-p = y가 0일 확률
• 왼쪽 항(logit(p)) :
  • 확률(0~1)을 (-∞ ~ +∞)로 늘린 값
  • 이 변환 덕분에 오른쪽의 선형식과 연결 가능
• 오른쪽 항 :
  • 입력 X들의 선형 조합
  • 그래서 이름은 ‘회귀’(regression) 이지만 실제 용도는 분류(classification)

계수 β의 의미는 무엇인가? — 오즈비(odds ratio)

우리가 최종적으로 구하는 것은 확률 p이므로 logit을 p로 다시 변환

이것이 시그모이드 함수다

결과는 어떻게 도출하는가?

• 예측된 확률이 임계값을 넘는지 그렇지 않은지를 확인해 분류를 진행함.
• 암계값을 0.5로 했을 때 예측된 확률 p=0.7로 나오면 1로 분류함.
• 🔥로지스틱 회귀의 최종 예측값은 1 혹은 0이다.

정리

① 로지스틱 회귀는 “확률을 예측하는 모델”이다. ⇒ 이진 분류 문제에 적용하는 모형
② 확률을 직접 선형식으로 예측할 수 없기 때문에 logit 변환을 사용한다.
③ 최종 출력은 시그모이드(sigmoid)를 통해 다시 확률로 변환된다.
④ 계수 β는 ‘오즈비(odds ratio)’로 해석한다.

모형 평가 지표

혼동행렬

예측값과 실제값을 비교해서 정답/오답 네 가지로 분류한 표

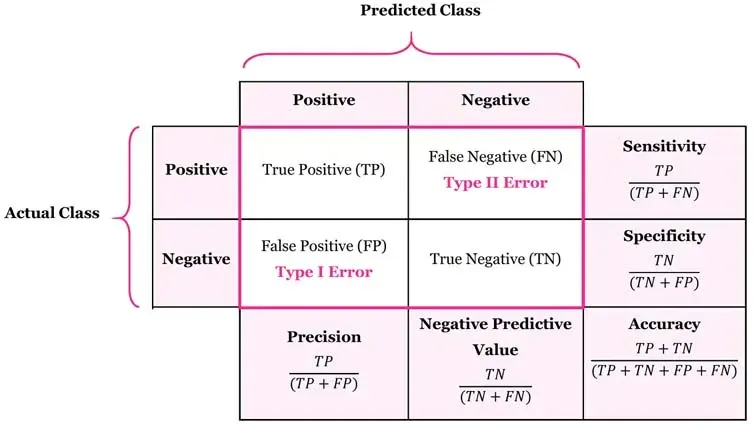
지표	설명	사용 상황
정확도(Accuracy)	전체 중 맞춘 비율	클래스 비율이 균형 잡혀있을 때
정밀도(Precision)	예측한 것 중 맞춘 비율	False Positive가 민감할 때
재현율(Recall)	실제 있는 것 중 맞춘 비율	False Negative가 민감할 때
F1-Score	정밀도와 재현율의 조화 평균	둘 다 중요할 때
ROC Curve, AUC	다양한 임계값에서 모델 성능 시각화	모델 전반 평가용

• ROC Curve : 분류 모델의 임계값 변화에 따른 TPR - FPR 관계를 시각화하는 그래프
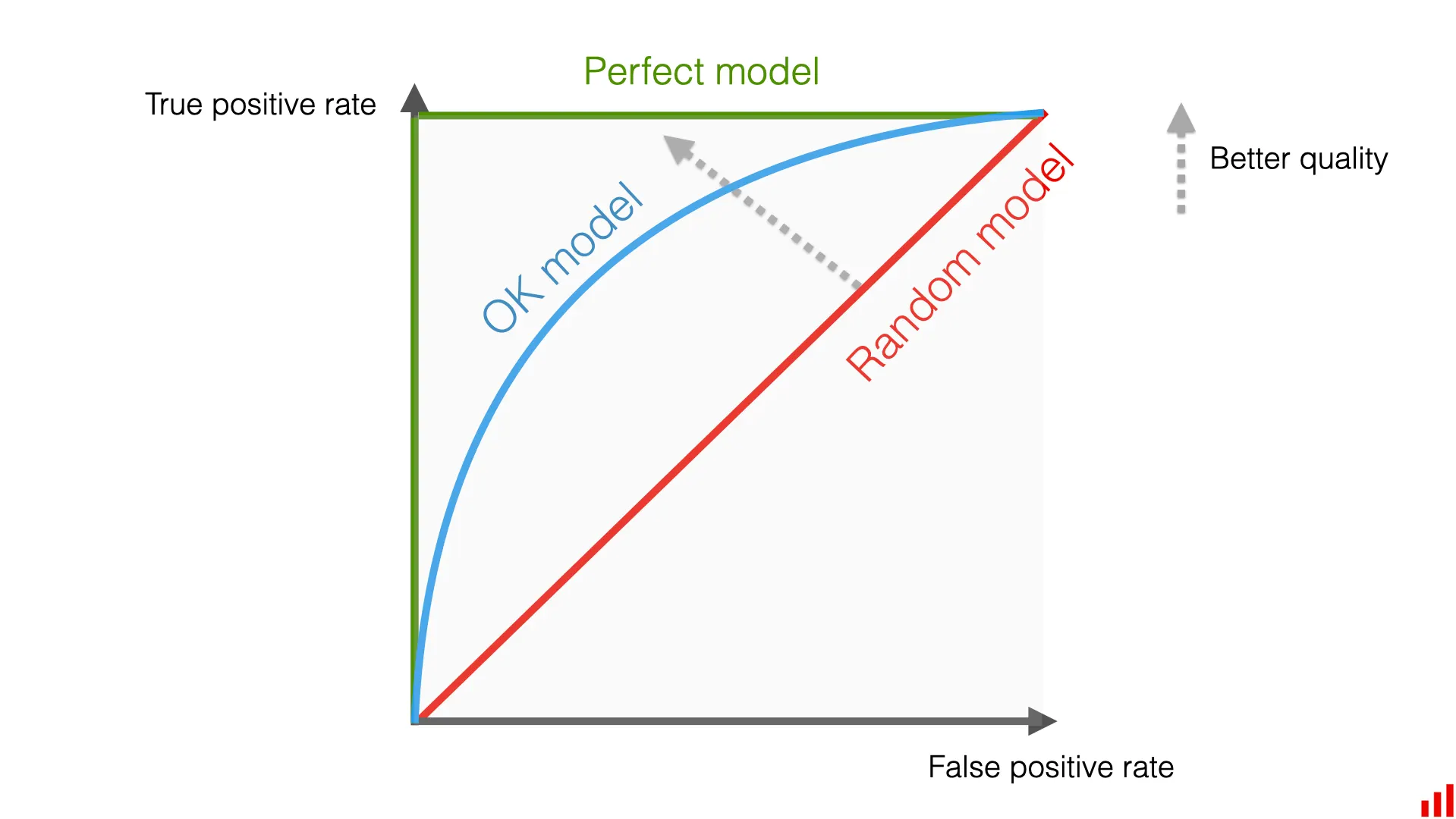
  • 왼쪽 위로 휜 곡선일수록 더 성능이 좋은 모델
    
• AUC : ROC 커브 아래 면적 (0.5 ≤ AUC ≤ 1)
  = AUC는 임계값에 영향을 받지 않고, 모델이 Positive와 Negative를 얼마나 잘 구분하는지 보여주는 가장 강력한 단일 지표

관련 코드

statsmodel 방법

statsmodel - 선형회귀

import statsmodels.api as sm

X = df_reg[['x1', 'x2', 'x3']] # 독립변수만 따로 추출
y = df_reg['y'] # 종속변수 선택

X = sm.add_constant(X) # X 데이터프레임 앞에 1로 채워진 'const' 컬럼(절편) 추가 
model = sm.OLS(y, X).fit() # 최소제곱법 회귀 모델 생성
print(model.summary()) # 회귀 분석 결과 전체 요약 출력

statsmodel - 로지스틱회귀

X = df_logit[['x1', 'x2', 'x3']]
y = df_logit['target']

X = sm.add_constant(X)
model = sm.Logit(y, X).fit() # OLS 대신 Logit을 쓴다는 점이 다름
print(model.summary())

scikit-learn 방법

선형회귀모델: LinearRegression

• 예측 및 평가

y_pred = model.predict(X_test)

mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

로지스틱회귀모델: LogisticRegression

• 혼동행렬로 모델 평가

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score

print("Accuracy :", accuracy_score(y_test, y_pred))
print("Precision :", precision_score(y_test, y_pred))
print("Recall :", recall_score(y_test, y_pred))
print("F1-score :", f1_score(y_test, y_pred))

3. 배운점

1. 분류 모델 중 로지스틱회귀 모델에 대해서 살펴봤다. 기존에는 개념만 알고 원리를 모른채 바로 LogisticRegression를 사용했지만 이번 기회에 원리도 살펴볼 수 있었다. 확률을 X값의 변화에 따른 선형관계로 나타내기 위해 오즈를 사용했고 선형 모델을 위해 로그오즈로 변환한 값을 y의 위치에 넣어 기존의 선형식과 결합을 한 것이다.
   이를 통해 최종적으로는 로그오즈에 있는 p(=확률)을 구하는 것이고 p를 좌측에 남기고 모두 오른쪽으로 넘겼을 때의 최종 p에 대한 공식이 바로 시그모이드 함수이다. 그리고 여기서 사용된 계수를 exp(β)로 하면 이게 오즈비가 된다.
   이렇게 말로 어느 정도 설명은 하고 오즈를 사용한 이유에 대해서도 살펴보긴 했지만 솔직히 1+1은 2이다 처럼 마음으로 와닿지는 않는다. 그냥 그렇다고 하니 그렇구나라고 인지만 하는 정도이다. 나는 이 정도의 수준을 '이해했다'라고 여기지는 않는다. 마음속에 뭔가 모를 꺼림직한 부분이 있기 때문이다.
   로그 오즈를 사용한 공식을 완성한 후 exp(β)를 취했을 때 오즈비의 값이 나왔기에 이것도 그렇구나라고 받아들였지만 처음 이 공식을 생각한 사람이 이것까지 의도한것인지 하다보니 이렇게 된건지 솔직히 모르겠다.
   나는 항상 이런 부분에 있어 스스로에게 굉장히 큰 불편함을 느낀다. 갑자기 나한테 해보라고하면 아무것도 없던 것에서부터 저 공식을 구현하는 논리 구조를 생각해내며 자연스럽게 해당 공식을 완성하는 것은 불가능 할 것 같기 때문이다. 내가 나에게 정의내리는 '이해'의 관점은 이런 것이기 때문에 무엇을 배우는 것에 있어 나를 내려놓기가 쉽지 않은 것 같다.

2. 혼동행렬
   머신러닝의 모델 평가에서도 자주 사용되고 실제 면접에서도 어떤 경우에 어떤 지표를 사용하는게 좋을지, 왜 해당 지표를 중요하게 생각했는지 물어볼 수 있기에 중요하다고 했다.