1. 학습 키워드

• 머신 러닝을 위한 전처리
• 파이썬 윈도우 함수

2. 학습 내용

데이터 전처리

데이터 전처리
원시(raw) 데이터에서 불필요하거나 손실(노이즈)이 있는 부분을 처리하고, 분석 목적에 맞는 형태로 만드는 과정

필요성

• 모델 정확도 및 신뢰도 향상
• 이상치나 결측치가 많으면 모델 성능이 떨어짐
• 효율적인 데이터 분석과 모델 훈련을 위해 필수적인 단계

결측치 처리 기법

• 삭제
• 대체: 평균 또는 중앙값으로 대체(분포 왜곡이 비교적 적음), 최빈값(범주형 데이터에서 사용)

# 2) 결측치 제거 (결측이 하나라도 있으면 해당 행을 제거)
df_drop = df.dropna()
df_drop

# 3) 평균값으로 대치
df_mean = df.copy()
# numeric_only = True: 숫자형 열에 대해서만 계산함.
df_mean = df_mean.fillna(df_mean.mean(numeric_only=True))
df_mean

mode()
: 각 열마다 최빈값을 구하기 때문에 여러개의 값이 나올 수 있다.

# 5) 최빈값으로 대치
#   - DataFrame의 mode()는 각 열별로 최빈값을 반환함.
#   - mode() 결과가 여러 개(동률)일 경우 첫 번째 행의 값을 취함.
df_mode = df.copy()
print(df_mode.mode()) # 확인용

mode_values = df_mode.mode().iloc[0]  # 첫 번째 행(가장 상위 mode)만 취함
df_mode = df_mode.fillna(mode_values)
df_mode

이상치 탐지 및 제거

1. 통계적 기법
   : 데이터가 정규분포를 따른다고 가정하고 평균에서 ±3σ(표준편차) 범위를 벗어나는 값을 이상치로 간주

2. 박스플롯
   : 사분위수(IQR=Q3-Q1)를 이용해 IQR-1.5xIQR, IQR+1.5xIQR을 벗어나는 데이터를 이상치로 간주

3. 머신러닝의 이상치 탐지 알고리즘
   ex) DBSCAN

정규화

MinMaxScaler
: 모든 값을 0과 1 사이로 매핑

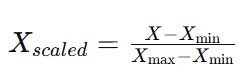
최소값, 최대값이 극단값에 민감. 만약 극단치가 있으면 대부분의 데이터가 [0, 1] 구간 한쪽에 치우침

표준화

StandardScaler
: 평균을 0, 표준편차를 1로 만듦

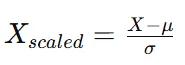
• 평균이 0, 표준편차가 1로 맞춰지므로 정규분포 가정을 사용하는 알고리즘에 자주 쓰임.
• 변환된 값들이 이론적으로 -∞ ~ +∞ 범위를 가질 수 있음.
• 데이터 분포가 심하게 치우쳐 있으면 평균과 표준편차만으로는 충분한 스케일링이 되지 않을 수 있다.

불균형 데이터 처리

모델이 극도로 적은 클래스를 거의 예측하지 못할 가능성이 큼(편향 발생)

해결 방법

1. Oversampling

• SMOTE: 소수 클래스를 무작정 복사하는 것이 아니라 비슷한 데이터들을 서로 섞어서 새로운 데이터 생성

2. Undersampling
   다수 클래스 데이터를 줄이는 방식

3. 혼합기법
   SMOTE와 Undersampling 적절히 섞어서 사용

범주형 데이터 변환

원-핫 인코딩: get_dummies() 사용

• 장점: 범주간 서열 관계가 없을 때 사용하기 좋음
• 단점: 범주가 너무 많으면 차원이 커짐

# 원핫 인코딩
pd.get_dummies(df, columns=['칼럼이름'])

레이블 인코딩

• 범주를 숫자로 직접 맵핑(M=0, L=1 등)
• 단순하지만 모델이 숫자의 크기를 서열 정보로 잘못 해석할 수 있음

# 범주형 변수 변환 (레이블 인코딩 예시)
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
df["label"] = encoder.fit_transform(df["label"])
df

피처 엔지니어링

모델 성능 향상을 위해 기존 데이터를 변형, 조합해서 새로운 특성(피처)을 만드는 작업

날짜 파생 변수

ex) 측정 시간이 ‘2025-02-24 10:35:00’이라면, ‘월(2)’, ‘요일(월=1)’, ‘시(10)’, ‘주말여부(0/1)’ 등으로 분해

수치형 변수 조합

ex) ‘온도’와 ‘습도’가 있을 때, 새로운 피처 ‘온도×습도(TEMP×HUMID)’를 추가

로그 변환, 제곱근 변환 등

분포가 매우 치우친 변수(오른쪽 꼬리가 긴 경우)에 로그 변환을 적용하여 정규성에 가까워지도록 조정

변수 선택

• 상관관계 파악 후 변수 선택
  두 변수 간 상관도가 높은 상황인 경우 다중공선성 의심. 중복 정보가 클 수 있으므로 하나만 남겨둠.

VIF

• 회귀 분석에서 다중공선성 문제를 파악할 때 사용함.
• 어떤 하나의 변수가 다른 변수들과 얼마나 겹치는지(상관이 큰지) 수치로 보여주는 지표.
• 10을 넘으면 해당 변수를 제거하거나 비슷한 변수를 합치는 방법으로 문제 해결

Feature Importance

• 트리기반 모델을 훈련 후 중요도가 낮은 변수를 제거

---

파이썬 윈도우 함수 라이브 세션 정리

shift

시계열 데이터의 인덱스를 원하는 기간만큼 이동시키는 메서드

DataFrame.shift(periods=기간, freq=None, axis=0, fill_value='비었음')

• df.shift(1).head() # 이전 값 땡김
• df.shift(-1).head() # 이후 값 땡김
• df.shift(periods=3,freq='D') # 3일 이동

rolling

데이터프레임 내 열에 대하여 일정 크기의 창(window, 범위)를 지정하여 그 window안의 값을 추가 연산을 통해 계산하는 메서드

DataFrame.rolling(window, min_periods=None, center=False, win_type=None, on=None, axis=0, closed=None, method='single')

• df.rolling(window=3).mean() # 3일 이동평균 구하기
• df.rolling(window=3).sum() # 3일 누적합 구하기
• df.rolling(window=3, center=Ture, closed='left').mean() # 3일 이동평균을 중간 행을 기준으로 계산하고, 왼쪽 값을 포함하여 계산

expanding

• 행이나 열의 값에 대해 누적으로 연산을 수행하는 메서드
• rolling은 범위를 지정해서 누적을 계산해 나가지만 expanding은 해당 행 or 열 까지의 모든 누적을 기준으로 연산을 수행한다.

df.expanding(min_periods=1, axis=0, method='single').추가메서드()

주요 파라미터

• min_periods: 연산을 수행할 요소의 최소 갯수입니다. 이보다 작으면 NaN을 출력
• axis : 연산할 축방향 설정. 0(행) / 1(열)
• method: 연산방식. single(연산을 한 줄씩 수행) table(전체 테이블에 대해서 롤링수행). 기본값 single , 롤링 연산할 경우 numba 라이브러리 추가로 import 필요.

데이터 타입별 상관관계

상관관계

• 두 변수간의 직선관계
• 상관관계는 원인과 결과가 아니다

1. 연속형-연속형

• 피어슨 상관관계
• df.corr(method='pearson')
• 상관계수(절대값) 해석
  0.9 ~ 1.0 매우 높은 음/양의 상관관계
  0.7 ~ 0.9 높은 음/양의 상관관계
  0.5 ~ 0.7 약한 음/양의 상관관계
  0.0 ~ 0.5 거의 상관관계가 없음

2. 연속형-범주형(이분형)

• 이분형 변수를 0과 1로 코딩한 다음에 피어슨 상관계수로 계산한 것(Point-Biserial Correlation)
• python scipy 라이브러리의 pointbiserialr 함수를 이용하여 수치를 계산

  주의점
  연속형 변수와 범주형 변수에 대한 상관관계를 해석할 때에는, 단순 통계량만 확인하는 것이 아닌, p-value(통계적으로 설명 가능한지) 를 함께 살펴보아야 함.(0.05 보다 작으면 우연히 발생한게 아니다)

3. 연속형-범주형(3개 이상)

• Polyserial correlation 또는 ANOVA검정 (분산 분석)
• Polyserial 상관분석: 범주형 변수가 순서형(1학년, 2학년, 3학년) 일 때 사용. 현재 파이썬에서 지원 안함.
• ANOVA: 범주형 변수가 명목형(데이터분석가, 화가, 의사, 교사)일 때 사용.
• ANOVA 검정은 python scipy 라이브러리의 f_oneway 함수를 통해 진행할 수 있음. F-Statistic 과 p-value 를 도출해 확인함.

검정통계량(F) 해석
F <1 무의미
1 <= F < 3: 거의 무의미
3 <= F <10: 경우에 따라 유의미
10 <= F < 50: 유의미(강한차이)
F > 50: 거의 확실한 유의미(아주 강한차이)
F >= 100: 확실한 유의미(매우 강한차이)

4. 범주형-범주형

• 파이 상관계수(Phi(φ) coefficient) 또는 Cramer's V
• 파이 상관계수는 두 범주형 변수를 0과 1로 코딩한 다음 → Pearson 상관계수를 구하는 방식으로, 각 범주형 변수가 2가지 값을 가지는 경우에만 사용할 수 있음. 따라서 Cramers'V를 사용하는게 좋다.

Cramers'V

• step1. 범주형 변수의 값들을 LabelEncoding
• step2. Cramers'V 함수 정의
• step3. 혼동행렬 생성

0 - 0.1 무시해도 되는 관계
0.1 - 0.2 약한 상관관계
0.2 - 0.4 보통의 상관관계
0.4 - 0.6 약한 상관관계
0.6 - 0.8 강한 상관관계
0.8 - 1.0 매우 강한 상관관계

아래의 함수 정의코드와 혼동행렬 코드에 적절한 값만 넣어서 상관계수 구하면 됨.

# step 02-03.함수 정의 및 혼동행렬 생성(define a function and make a confusion matrix)

def cramers_V(var1,var2) :
    crosstab =np.array(pd.crosstab(var1,var2, rownames=None, colnames=None)) # Cross table building
    stat = chi2_contingency(crosstab)[0] # Keeping of the test statistic of the Chi2 test
    obs = np.sum(crosstab) # Number of observations
    phi2 = stat / obs
    r, k = crosstab.shape
    phi2corr = max(0, phi2 - (((k-1)*(r-1))/(obs - 1)))
    rcorr = r - ((r-1)**2)/(obs-1)
    kcorr = k - ((k-1)**2)/(obs-1)
    return np.sqrt(phi2corr / min((kcorr-1), (rcorr-1)))

rows= []

for var1 in data_encoded:
    col = []
    for var2 in data_encoded :
        cramers =cramers_V(data_encoded[var1], data_encoded[var2]) # Cramer's V test
        col.append(round(cramers,2)) # Keeping of the rounded value of the Cramer's V  
    rows.append(col)
cramers_results = np.array(rows)
data_encoded_df = pd.DataFrame(cramers_results, columns = data_encoded.columns, index =data_encoded.columns)

data_encoded_df

---

통계 라이브 세션 정리

표준오차(standard error) ⭐️⭐️

• $SE = \frac{σ}{\sqrt{n}}$
• 표본평균이 얼마나 흔들리는가(변동성)를 나타내는 지표 = 표본평균의 표준편차
• 표본이 커질수록 표준오차는 작아진다.
• 현실에서는 σ를 모른다 → 표본표준편차 s로 SE를 추정

표본평균의 분포

• 표본평균은 표본마다 달라도, 그 ‘분포’는 일정한 규칙을 가진다.
• 모집단이 정규가 아니어도 표본크기 n이 충분히 클 때(중심극한정리) 표본평균의 분포는 정규분포로 근사된다.

중심극한정리
모집단의 분포가 어떻게 생겼든 상관없이, 표본을 여러 번 뽑아서 각 표본의 평균을 계산하면 그 평균들은 정규분포 형태로 모이게 된다.

왜 정규성 가정이 중요할까?
정규분포가 아니면 표본평균의 분포가 어떻게 생겼는지 알 수 없기 때문에 p-value, 신뢰구간, Z-test·t-test 같은 통계적 추론 공식들이 성립하지 않는다.

< 기억할 3가지 >

• 앞으로 배울 많은 통계 기법들이 정규 분포를 기반으로 만들어졌다는 것
• 모집단이 정규가 아니어도 중심극한정리가 표본평균을 ‘정규에 가깝게’ 만들어주기 때문에 실제 분석이 가능하다는 것
• 그럼에도 표본이 너무 왜곡되어 있거나 이상치가 많은 경우에는 주의해야 한다는 것

신뢰구간

• 단 하나의 숫자로는 불확실성을 담을 수 없음. ⇒ 모수가 존재할 법한 범위(구간)를 제시하는 것이 필요!
• 구간추정: 신뢰 가능한 범위를 제시함. (ex 모집단의 평균은 62~68 사이일 것이다)
• 95% 신뢰구간 : 반복해서 표본을 추출하고 신뢰구간을 만들면, 그 중 95%가 𝜇(모집단의 평균)를 포함하게 될 것이다.

Z분포 기반 신뢰구간

• Z-분포는 평균 0, 표준편차 1인 정규분포(표준정규분포) 정규분포를 표준화하면 언제나 Z-분포가 된다.
• 모집단의 표준편차 σ를 알고 있을 때, 표본평균의 상대적 위치를 Z값으로 계산할 수 있다.

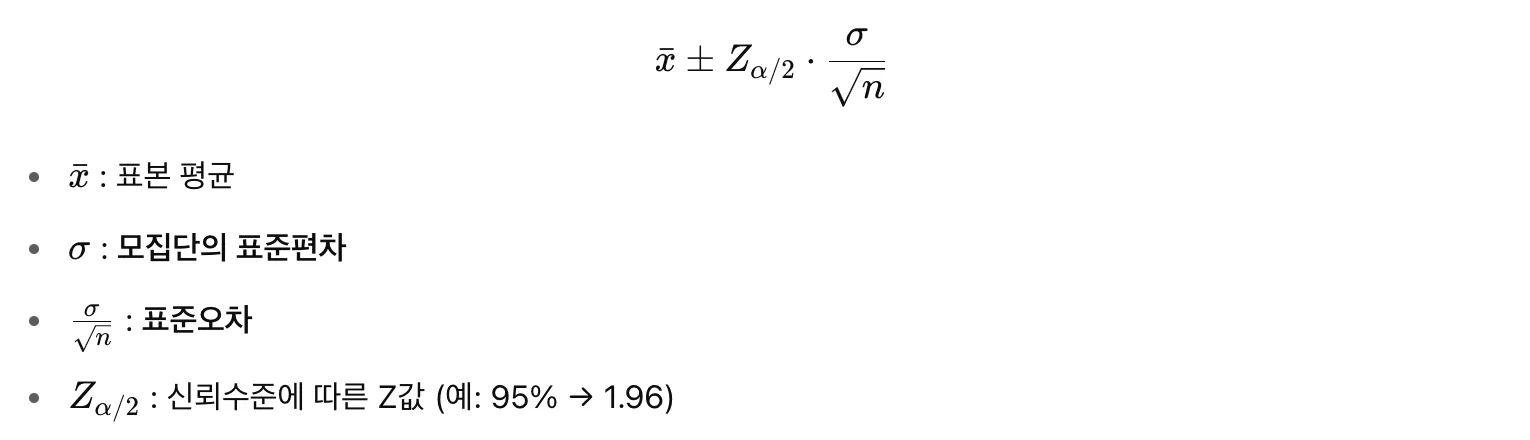
⇒ 대부분 모집단의 표준편차 σ를 모르기 때문에 표본에서 계산한 표준편차 s로 대신하고 t-분포를 쓴다!

t분포

• σ를 모르기 때문에 s를 사용할 때, 추가적인 불확실성을 반영해주는 분포가 t-분포

⇒ t-분포는 모집단의 σ를 모른다는 현실을 반영하는 분포. 표본 크기 n이 커지면 s가 σ에 가까워져, t-분포는 점점 Z-분포와 동일해진다.

가설검정

어떤 주장이 통계적으로 의미가 있는가?’를 판단

• 귀무가설(H₀): 밝히고자 하는 가설의 부정 명제 : 두 그룹의 클릭률 차이는 없다 (즉, 차이 = 0)
• 대립가설(H₁): 밝히고 싶은 가설 : 두 그룹의 클릭률 차이는 있다 (즉, 차이 ≠ 0)
  검정통계량: (A - B)의 차이를 표준오차로 나눈 값
  유의수준 α: 보통 0.05 (5%)
  p-value: 실제 데이터에서의 차이가 우연히 나올 확률
  판단 기준: p-value < 0.05 → H₀ 기각 (차이 유의함)

🔥 p-value

귀무가설이 맞다고 했을 때 지금 관측한 데이터가 나올 확률(우리가 관측할 확률)

현실의 데이터가 귀무가설(H₀)이 맞는 세상에서 나올 수 있는 값일까? → 가능성의 정도 : p-value

• p-value가 작다 → “이런 데이터는 귀무가설이 맞다면 거의 나오지 않는다.” → 귀무가설 기각
• p-value가 크다 → “이런 데이터는 귀무가설이어도 자주 나올 수 있다.” → 귀무가설 유지

유의수준(α)과의 관계

• 유의수준 α: 기준선 역할을 하는 값. 보통 0.05 (5%) 사용 (=귀무가설 채택 기준)
• p-value < α → 귀무가설 기각
• p-value ≥ α → 귀무가설 기각 못함

⇒ 귀무가설을 기각하는 경우 “통계적으로 유의미한 차이가 있다.”고 표현

주의

• p-value는 귀무가설이 참일 확률이 아니다!
• 단지 “귀무가설이 참일 때 지금 데이터가 얼마나 극단적인지”를 나타낸다.
• 기각한다는 것은 “차이가 있다고 보기로 결정할 근거가 충분하다”는 의미

양측검정 vs 단측검정

‼️ 실무에서는 대부분 양측검정을 사용. 사전 지식 없이 A가 B보다 낫다고 주장하는 건 위험할 수 있다!

제1종 오류(False Positive)

• 사실은 효과가 없는데(귀무가설이 맞는데), 있다고 판단하는 오류
• 발생 확률 = 유의수준(α) → 보통 0.05 (즉, 5%)

제2종 오류(False Negative)

• 사실은 효과가 있는데(대립가설이 맞는데), 없다고 판단하는 오류
• 발생 확률 = β (베타) ↔ 발생하지 않을 확률 = 1 - β (검정력)

3. 배운점

1. 이전에 콘텐츠 조회수 예측 프로젝트를 하면서 변수 중요도를 산출해 본적이 있다. 당시에는 변수 중요도를 정확히 어떤 상황에서 산출하는지 몰라 원-핫 인코딩된 컬럼이나 회귀 모델에서 무작정 산출해 보면서 이상하다는 생각을 했었는데 변수 중요도는 주로 트리 기반 분류 모델에서 사용하는 것임을 다시 한 번 알게됐다.

2. 시계열 데이터를 다루기 위한 파이썬 함수 shift(이전, 이후값 가져오기), rolling(범위를 지정해 누적을 계산), expanding(전체의 누적을 계산)에 대해 알 수 있었다.

3. p-value는 귀무가설(차이가 없다)이 맞다고 했을 때 대립가설(우리가 관측한 값)이 우연히 발생한 확률을 나타내는 것으로 일반적으로 0.05 이하이면 우연이 아니라는 뜻. 한마디로 차이가 있다는 것을 의미함.

4. z분포 기반 신뢰구간에서 무조건 표본 평균을 사용해야만 하는것이 아니다. 우리의 추정값(통계량)을 사용하는 것이다.