확률
표본 공간(Sample Space)
- 어떤 실험에서 나올 수 있는 모든 가능한 결과들의 집합
통계적 확률 정의
- 어떤 시행을 N 번 반복했을 때, 사건 A에 해당하는 결과가 R 번 일어난 경우 r/N 이고, 사건 A가 일어날 상대도수라고 함.
- N이 무한히 커지면 상대도수는 일정한 수로 수렴하는데, 이 극한값을 사건 A의 통계적 확률 또는 경험적 확률 이라고 함.
ex) 동전을 던져서 앞면이 나올 확률 -> 1/2
확률의 성질
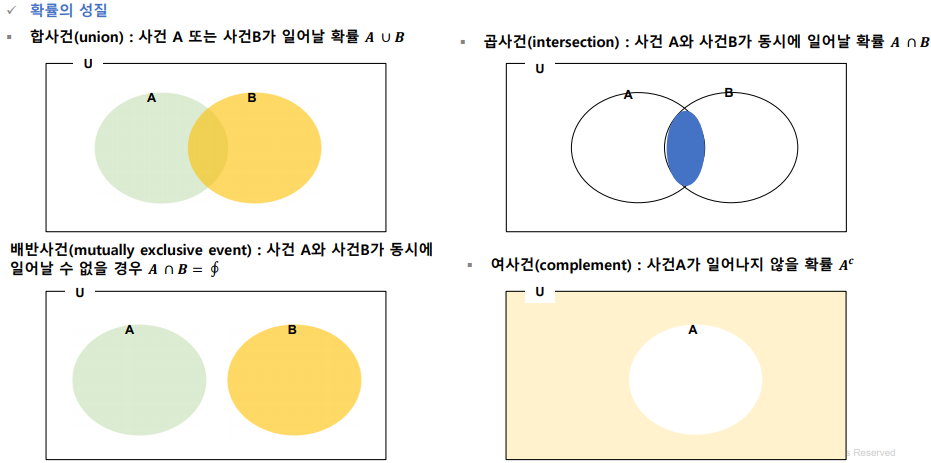
조건부 확률
베이즈 정리
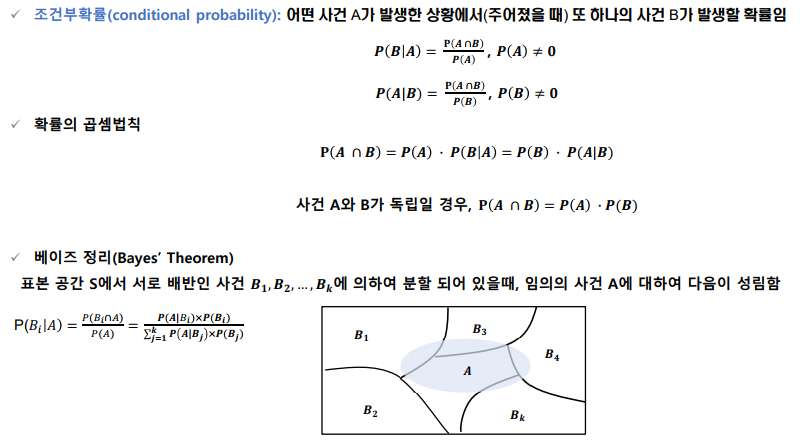
b) 문제가 베이즈 정리에 해당함

확률변수
- 확률변수: 표본공간에서 각 사건에 실수를 대응시키는 함수를 확률 변수라고 함.
- 확률 변수의 값은 하나의 사건에 대하여 하나의 값을 가지며, 실험 결과에 의하여 변함.
- 일반적으로 확률 변수는 대문자로 표현, 확률 변수의 특정값을 소문자로 표현

확률 변수의 평균: 기대값

분산
- 확률 변수의 분산은 x제곱의 기대값 - x의 기대값의 제곱

확률 분포
확률변수 x가 취할 수 있는 모든 값과 그 값을 나타날 확률을 표현한 함수
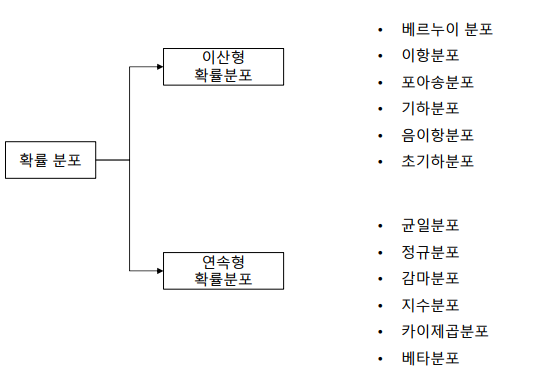
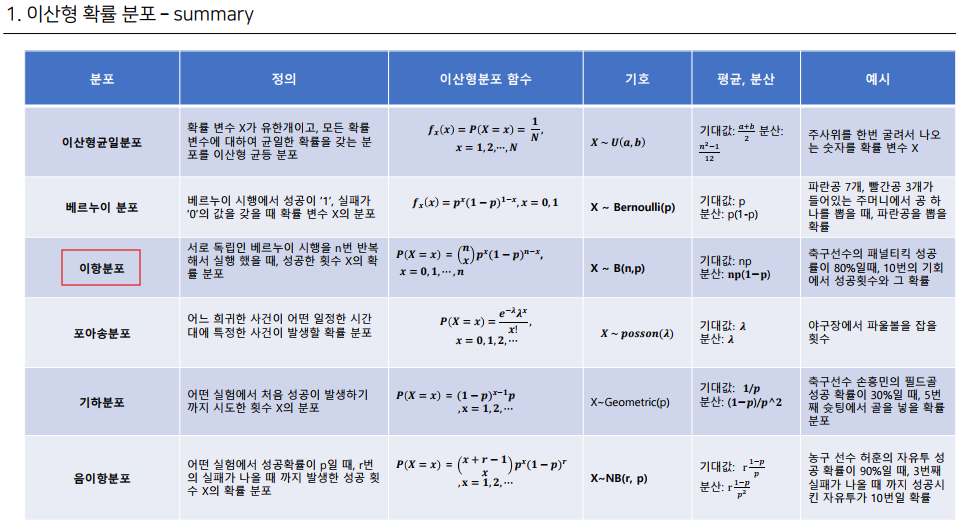
이산형 확률분포
이산형 균등 분포
확률 변수 x가 유한개이고, 모든 확률 변수에 대하여 균일한 확률을 갖는 분포
ex) 주사위 굴려서 숫자가 나올 확률

베르누이 분포
베르누이 시행: 각 시행의 결과가 성공, 실패 두가지 결과만 존재하는 시행을 베르누이 시행이라고 함.
베르누이 분포의 평균: P, 분산 P(1-P) 그냥 외우기

이항분포
이항분포: 연속적인 베르누이 시행을 거쳐 나타나는 확률 분포
서로 독립(공을 하나 뽑고 연속해서 더 뽑는게 아니라 공을 다시 넣고 다시 뽑는 것이 독립의 의미)
이항분포의 평균: np
이항분포의 분산: npq -> q = 1-p 이므로 np(1-p)


포아송 분포
포아송 분포: 어느 희귀한 사건이 어떤 일정한 시간대에 특정한 사건이 발생할 확률 분포


이항 분포의 포아송 근사
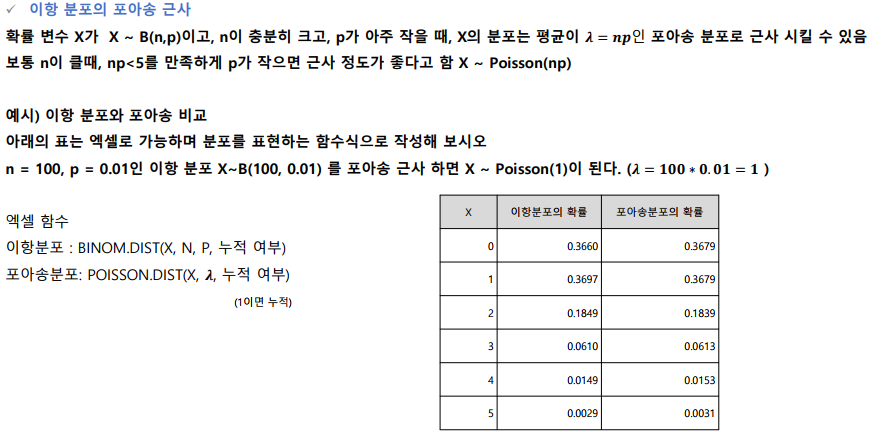
기하 분포
기하분포: 어떤 실험에서 처음 성공이 발생하기까지 시도한 횟수 x의 분포, 이때 각 시도는 베르누이 싱행을 따름

음이항분포
어떤 실험에서 성공확률이 p일 때, r번의 실패가 나올 때 까지 발생한 성공 횟수의 x의 확률분포

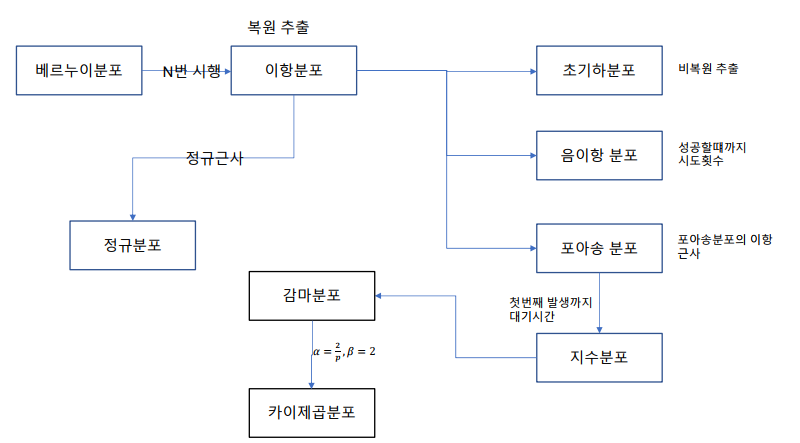
요약
베르누이 분포를 n 번 반복하면 이항분포
연속형확률분포
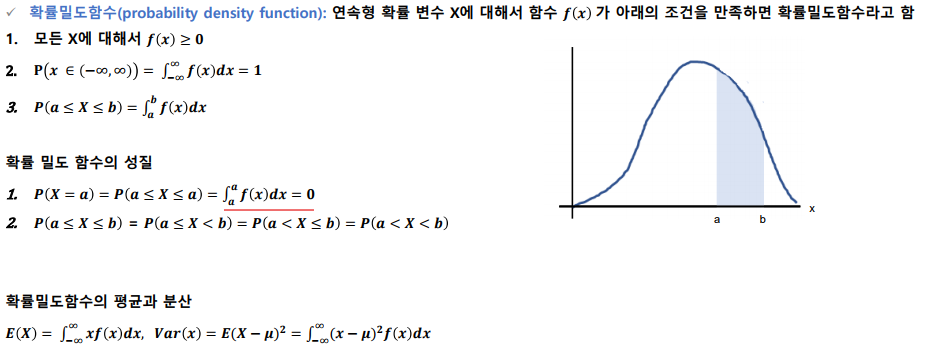
확률밀도함수(pdf)
누적분포함수(cdf)
확률밀도함수를 적분하면 누적분포함수가 됨
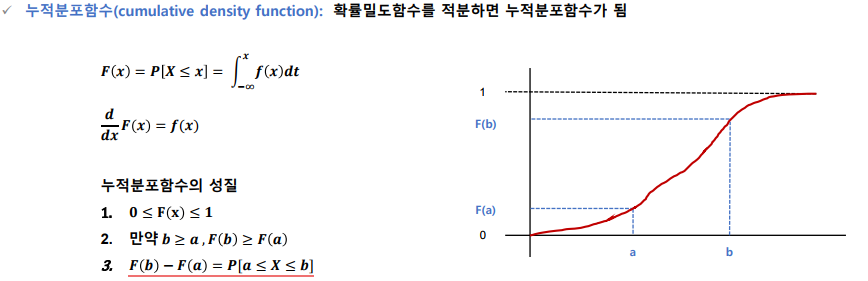
F(b) - F(a): 확률 x가 a와 b사이에 있을 확률이다.
균일분포
확률 변수 x가 a와 b사이에서 아래와 같은 확률 밀도 함수(pdf)를 가짐

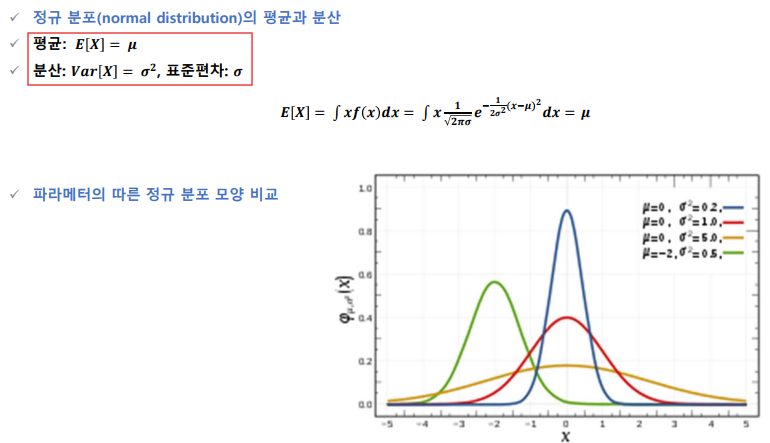
정규분포 **
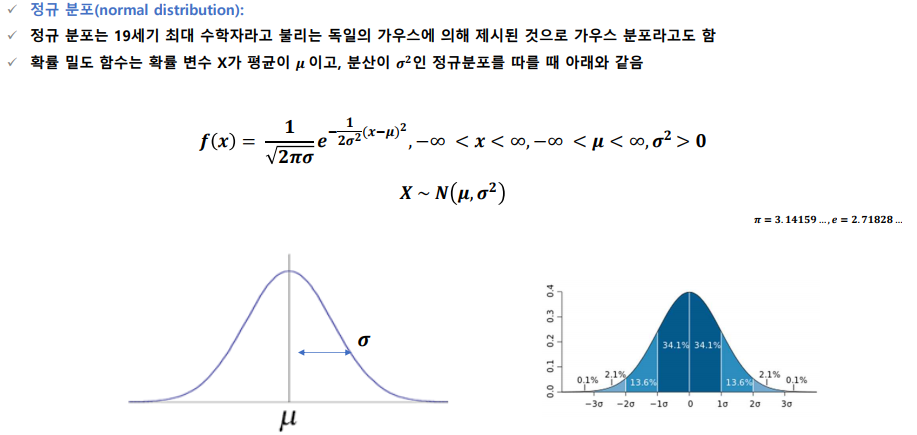
- 중심이 μ(평균)이 된다.
- 좌우 대칭이다.
- 면적의 합 = 1
- σ = 편차
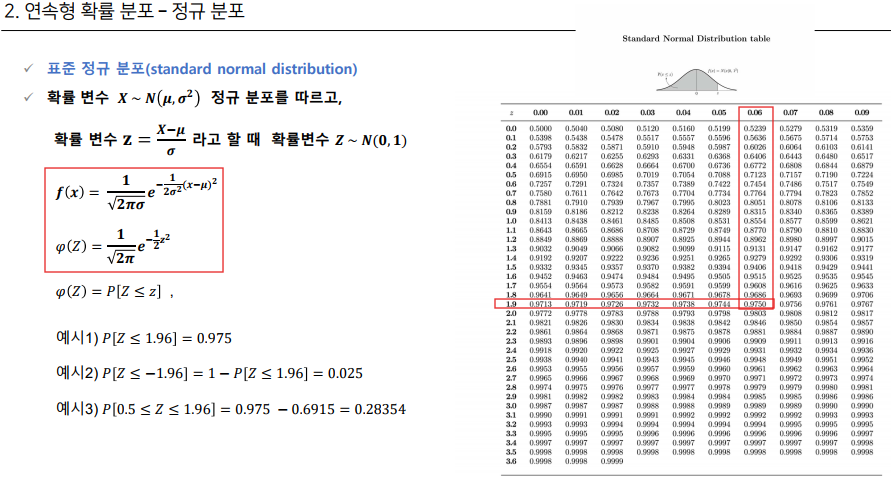
표준 정규 분포
분포를 표준화해서 비교한다.
성질이다른 것들을 표준화 해서 비교한 뒤에 다시 원래대로 돌림.
ex) 섭씨와 화씨를 그대로 비교할 순 없으니 표준화 해서 비교 한 뒤에 다시 원래 값으로 돌림.
시그마 = 1, 평균 = 0으로 표준화

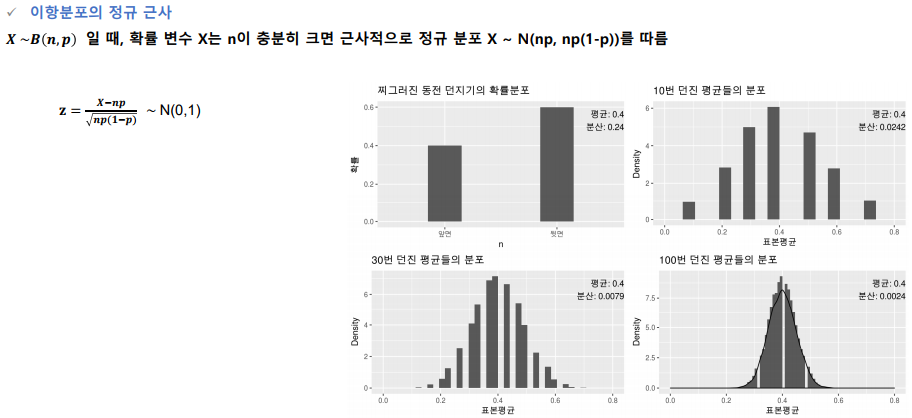
B(n,p): 이항분포
N(μ, σ^2): 정규분포
'이항분포는 n 이커질수록 정규분포에 가까워진다' 는 뜻
이항분포의 평균 np -> 정규 분포의 평균 μ
이항 분포의 분산 np(1-p) -> 정규 분포의 분산 σ^2
-> 평균이 np, 분산이 np(1-p)인 정규 분포로 근사할 수 있다.
연속형 확률 분포 - 실습

엑셀에서 정규 분포를 구하는 함수: NORM.DIST
(예시5)엑셀에서 z알파의 값을 찾는 함수: NORM.INV
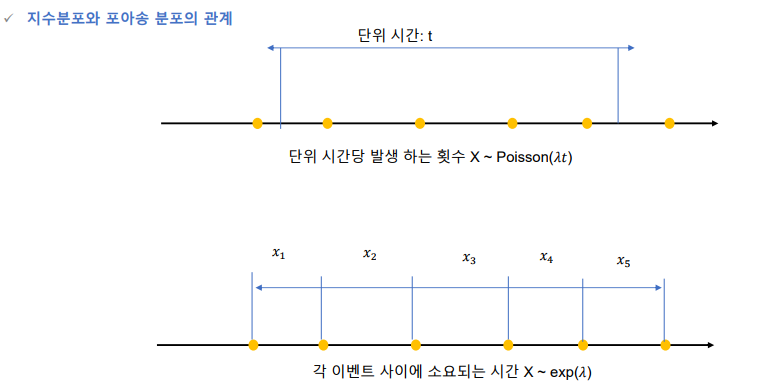
지수분포
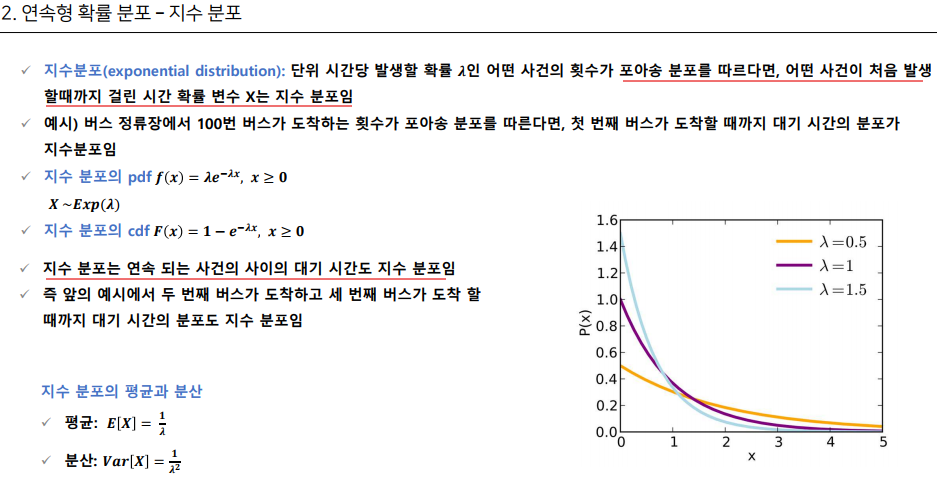
람다: 단위 시간당 이벤트가 발생하는 수

지수분포의 무기억성

모집단과 표본 분포
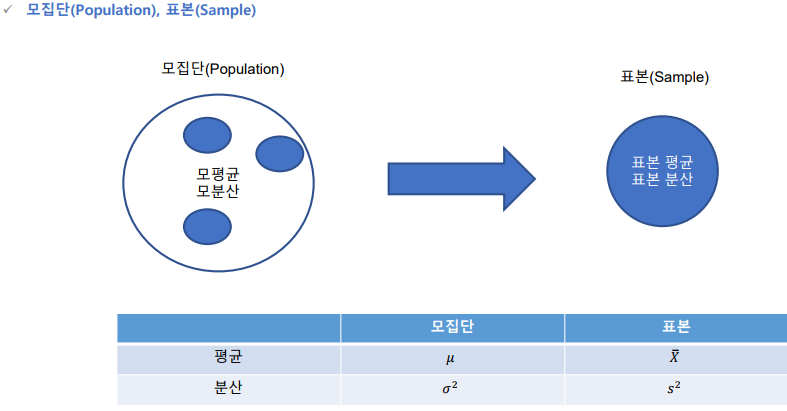
표본추출
모집단으로 부터 표본을 추출하는 것을 sampling이라고 한다.
sampling이라는 말을 많이 씀.

샘플링을 할때 발생하는 문제

샘플링기법

과도적합: 샘플링한것들을 다 맞춰가려고 하는 것임.
표본 분포
통계량

S^2 은 편차의 제곱의 합을 (n-1)로 나눈 것
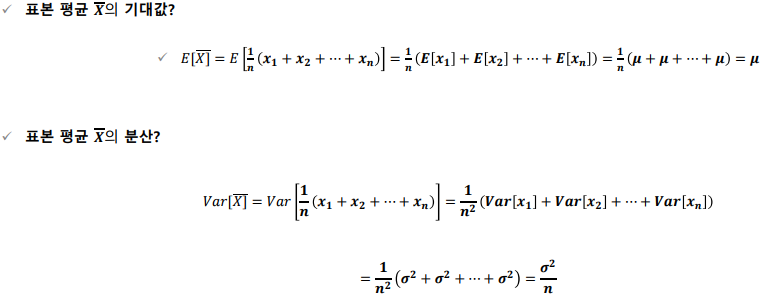

iid: 모든 표본은 서로 독립이고 동일한 분포에서 뽑는다
중심극한정리**(면접에 정의 나오기도 함)
표본이 충분히 크면 정규분포를 따른다

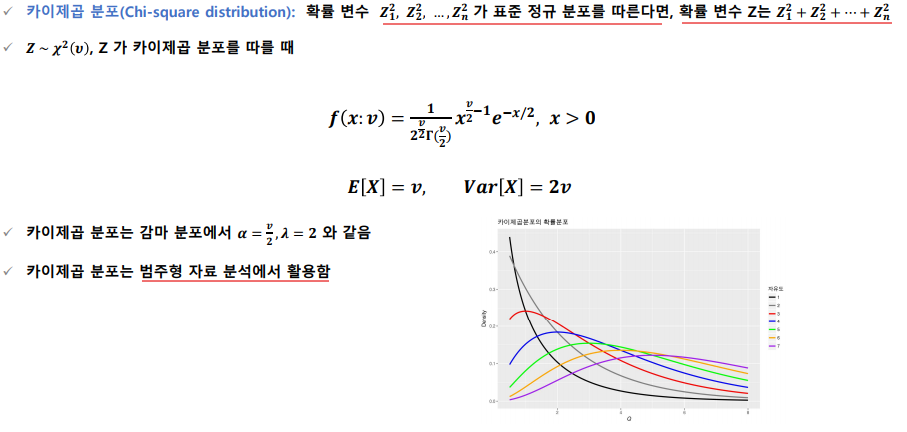
카이제곱분포
분산분포, 회귀분포에서도 이 개념을 사용함.
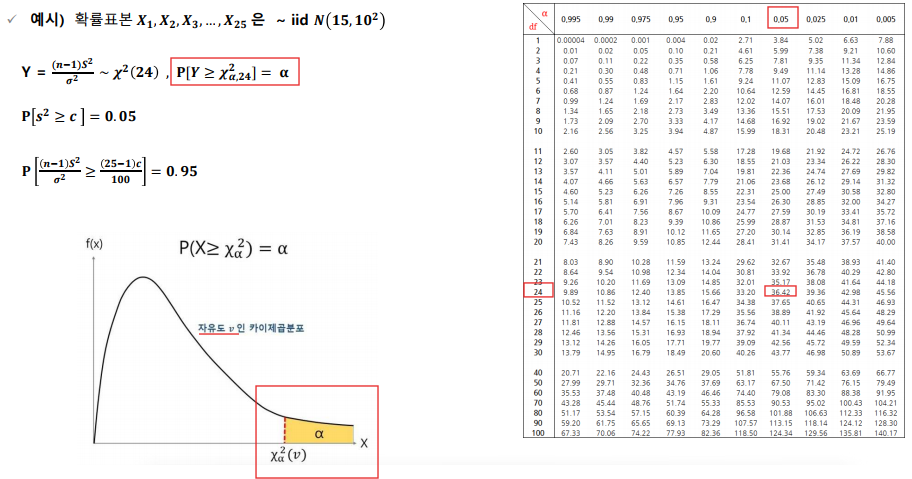
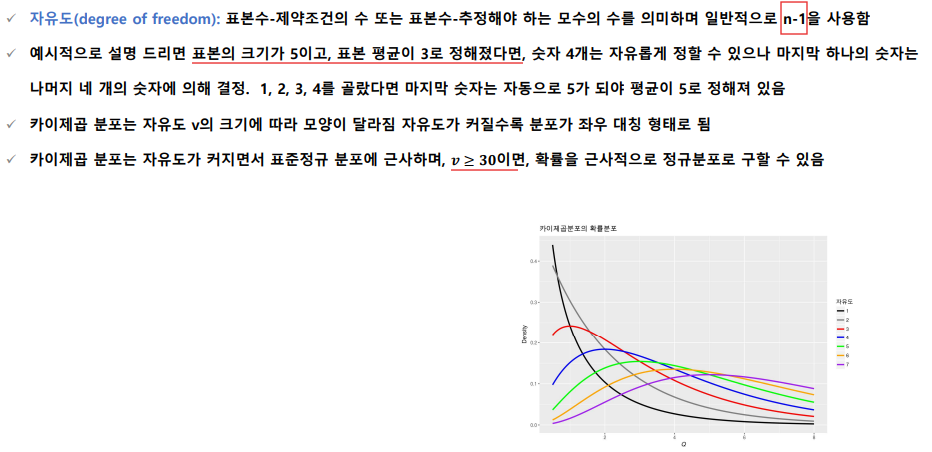
자유도
표본 크기가 5, 표본 평균이 3이면 만약 숫자가 1,2,3,4로 정해져있다면 마지막 5번째 숫자는 5여야만 표본 평균이 3이됨.
t분포 **
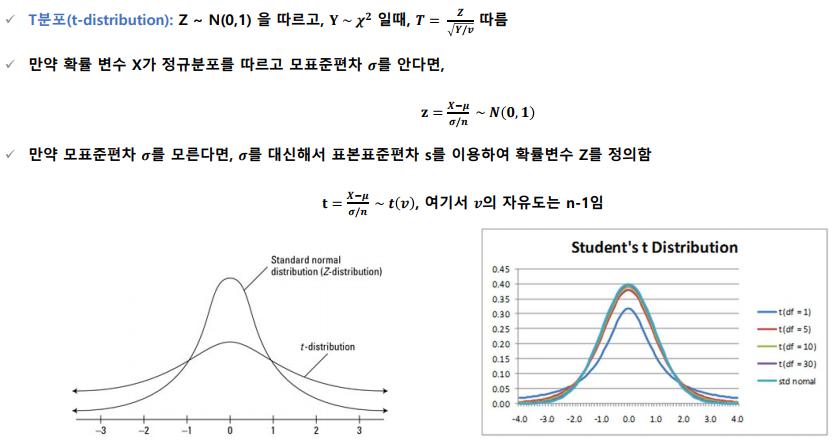

F분포

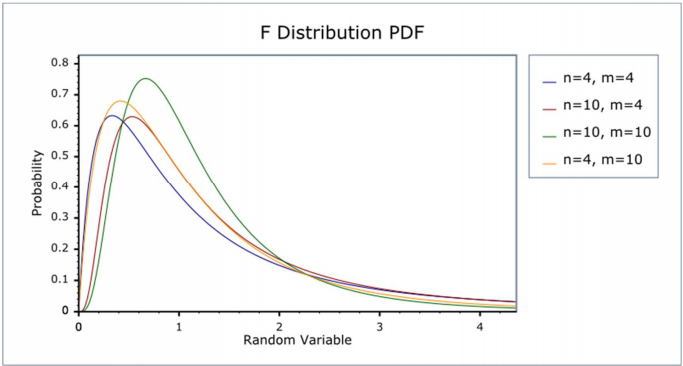

추정



알파는 오차
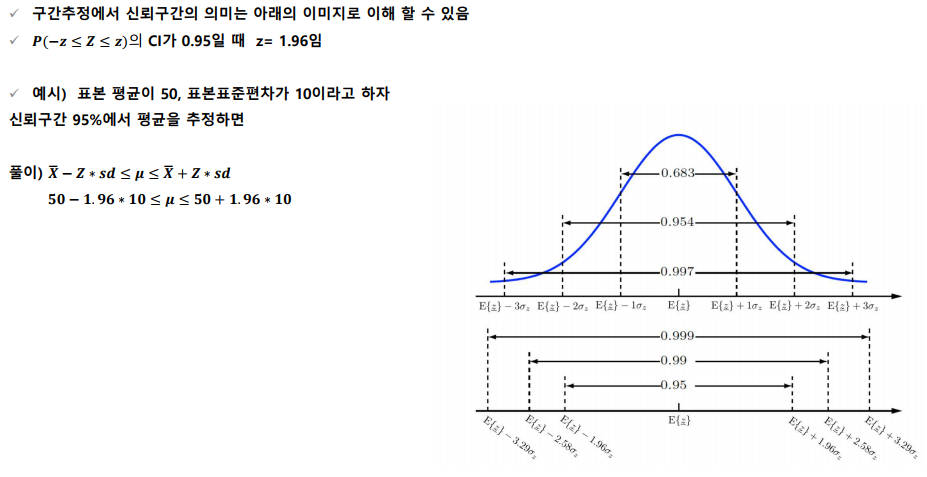
모평균의 구간 추정

모집단의 분산을 모르는 경우 t분포를 사용한다.
밑에 오타: t0.25 -> t0.025


모비율의 추정
계속 모니터로만 공부하기 어려워 이후 통계 부분은 종이 필기로 대체
