데이터 취업 스쿨 스터디 노트 -(48) 머신러닝, dicision tree, scikit learn, accuracy, zip

Decision Tree

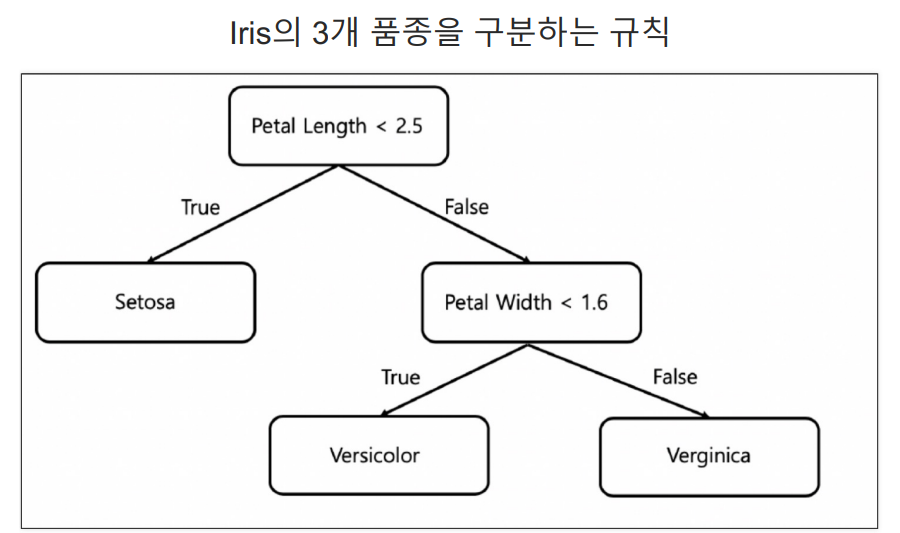
분할 기준

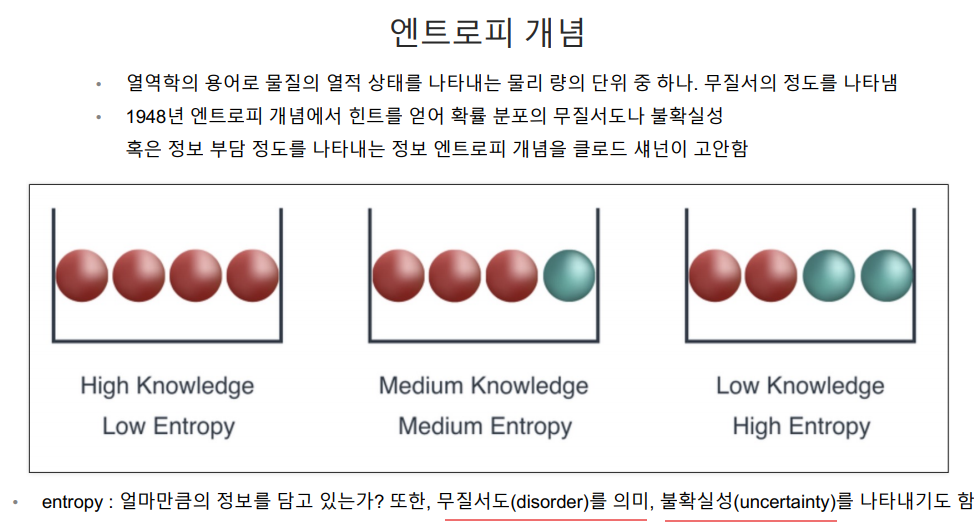
데이터 분석 영역에서는 엔트로피가 높다는 것은 무질서도가 높다는 의미.

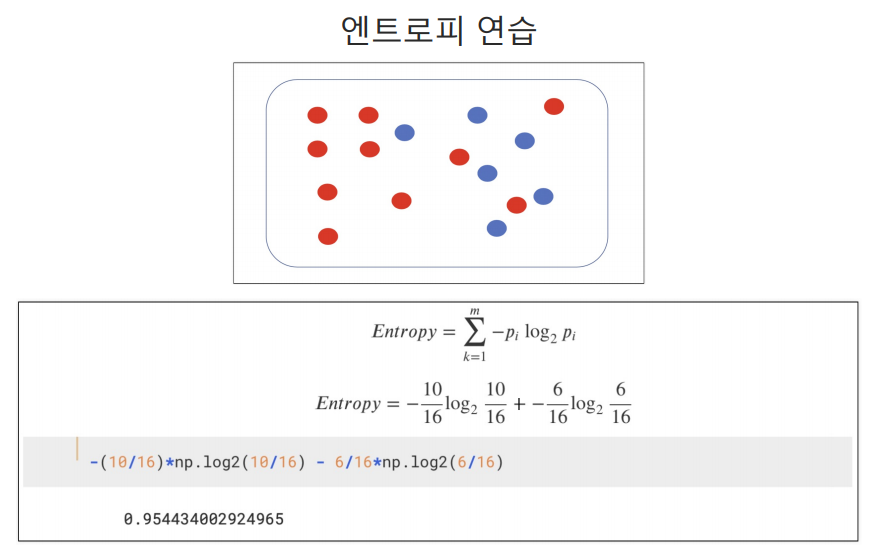
빨간색 공은 10개, 파란색 공은 6개

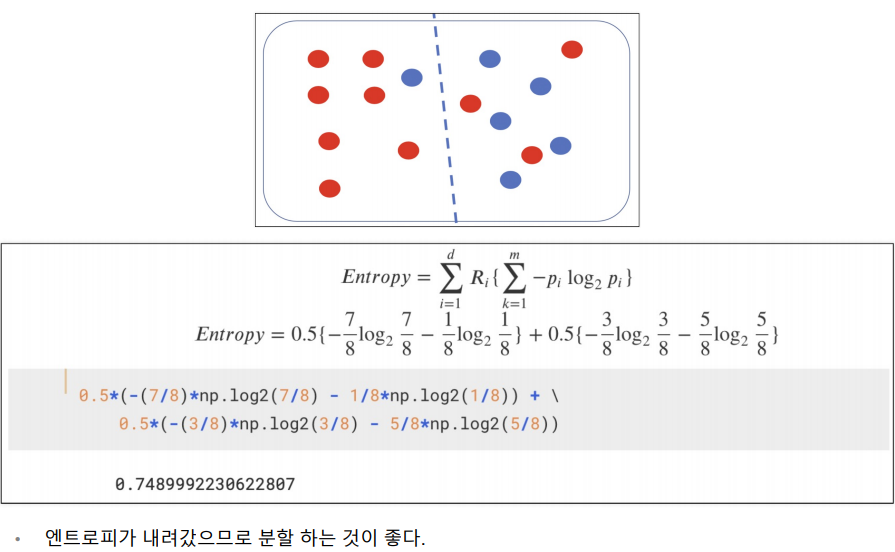
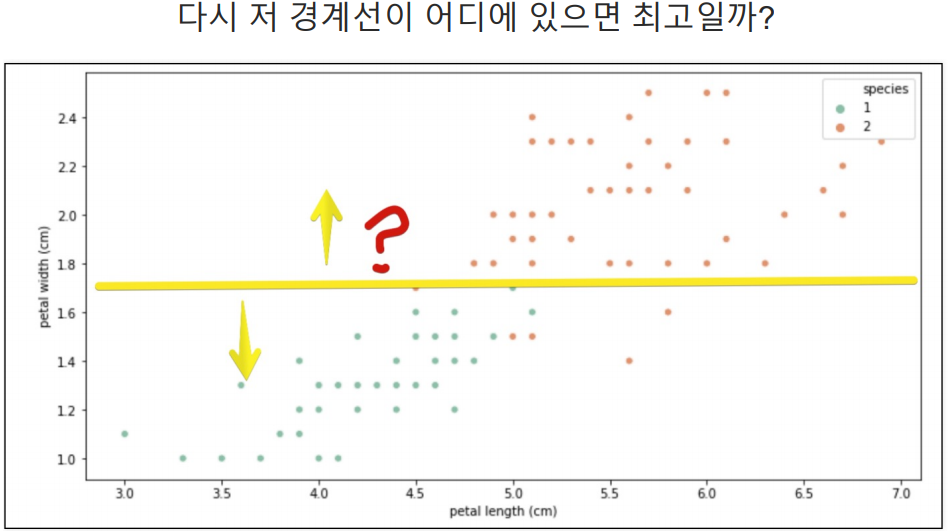
왜 나누는 기준점을 여기로 잡은거야?
다른 곳을 기준점으로 잡아서 나눠도 되잖아?
기준점을 잡은 근거를 위해 '지니계수'를 사용함.
지니계수가 낮기 때문에 무질서도가 낮아 더 잘 분류했다고 할 수 있기 때문이다.

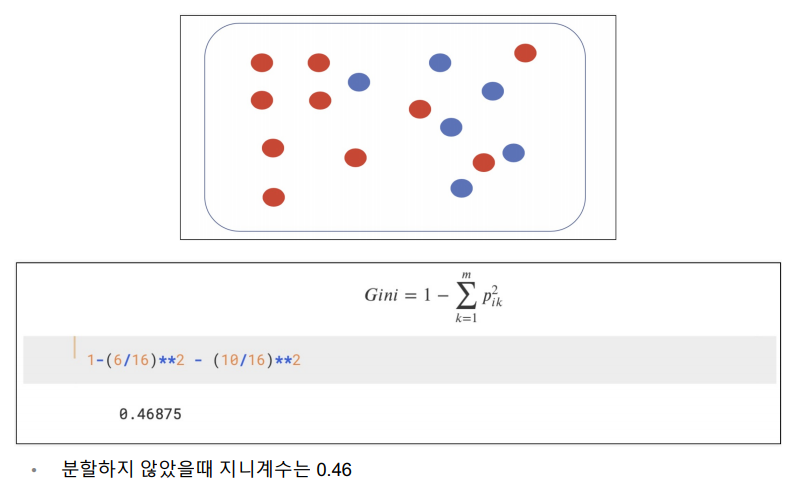
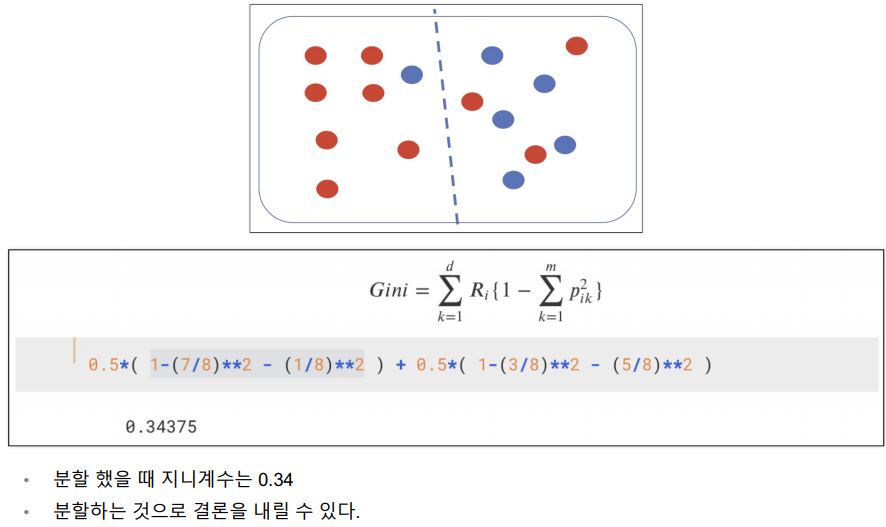
그렇다면 IRIS 데이터에서 품종을 나누는 기준은 어떻게 잡는것이 좋을까?

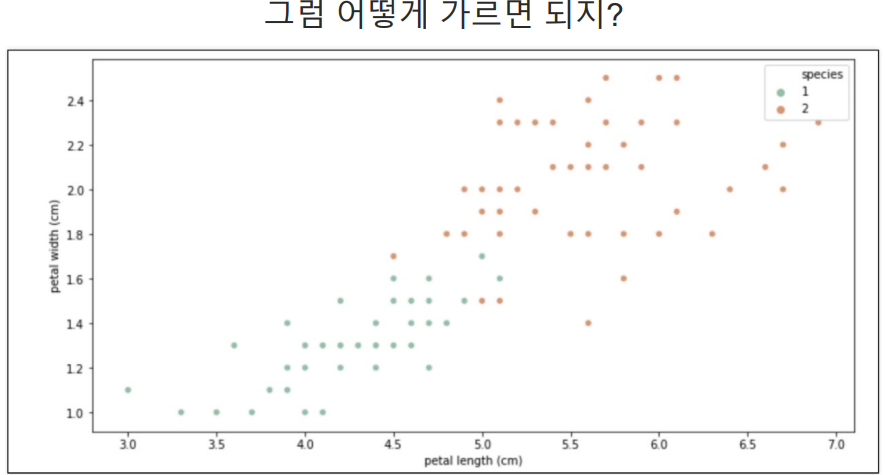
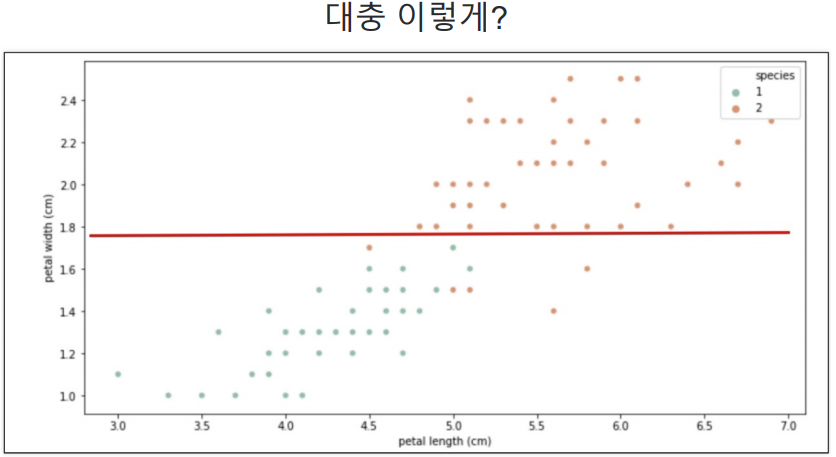
과거에는 위의 기준점을 계속 하나씩 변경하면서 직접 코딩을 했지만 지금은 프레임워크가 있다. 그 프레임워크가 Scikit Learn 이다.

Scikit Learn

from sklearn.tree import DecisionTreeClassifier
#
iris_tree = DecisionTreeClassifier()
iris_tree.fit(iris.data[:, 2:], iris.target)
# fit: 학습을 해라, fit(학습할 데이터, 정답)

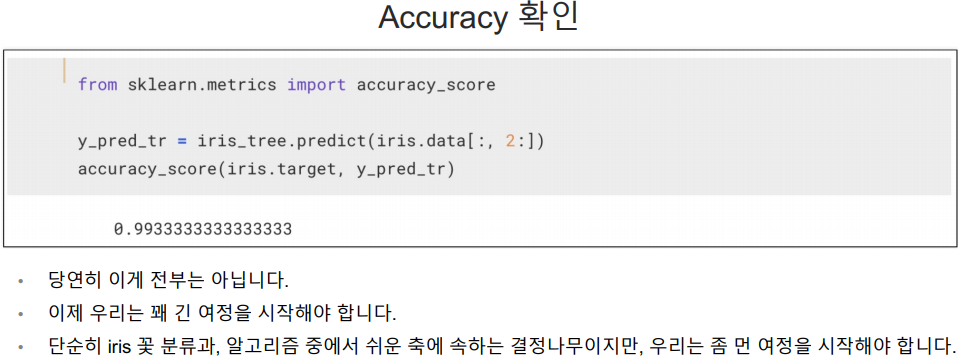
위 코드를 통해 학습이 완료됨.
그리고 학습한 내용을 바탕으로 예측을 진행(predict() 함수)
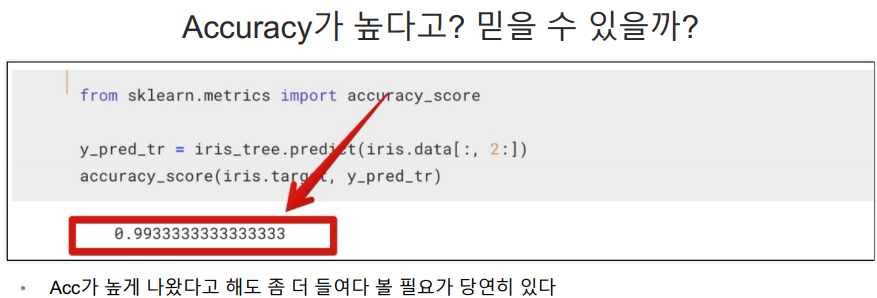
accuracy_score(정답, 예측한 결과) : 얼마나 정확성이 있는지 알려줘.

과적합

내가 가진 모델에만 너무 적합한 모델

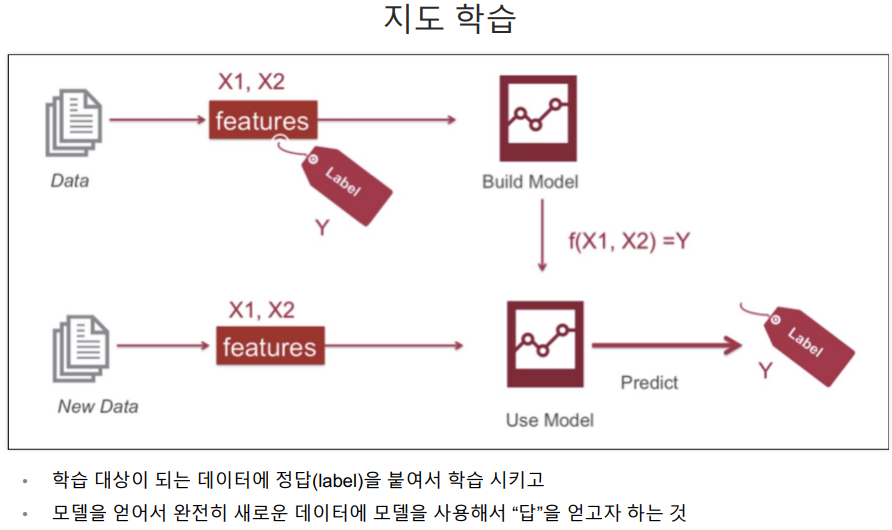
위의 과정들은 정답을 알려주고 학습을 시키는 '지도학습'이었다.

참고)

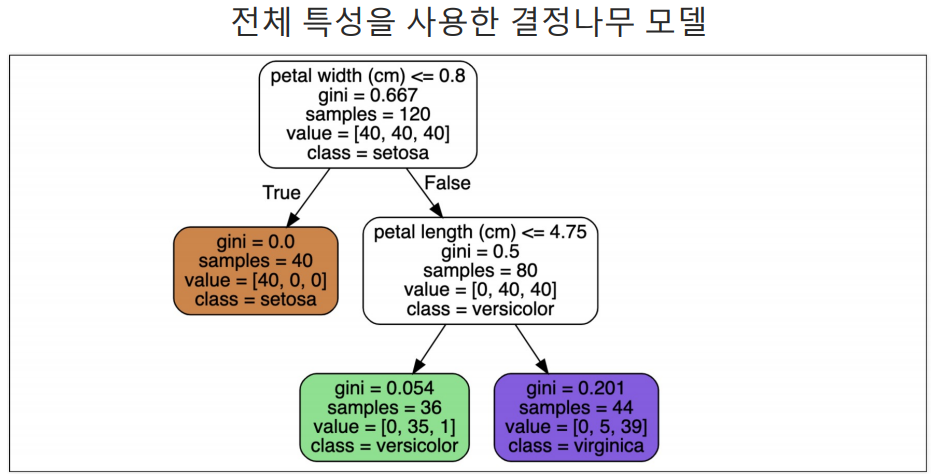
from sklearn.tree importy plot_tree
plt.figure(figsize=(10,12))
plot_tree(iris_tree)

plot_tree(학습결과)라는 함수는 내가 학습시킨 모델의 decision tree를 보여주는 함수이다.

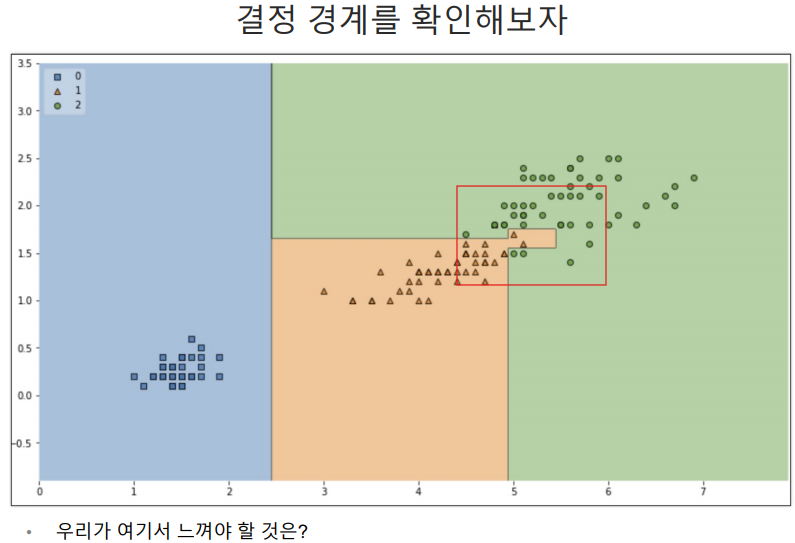
복잡한 경계면 덕분에 위에서 accuracy가 99.3%가 나온 것이다.

내가 가진 데이터에만 너무 적합해지면 해당 머신러닝 모델은 일반적인 성능을 가질 수 없다. 그것을 '과적합'이라고 한다.
이 과적합을 주의해야 한다.

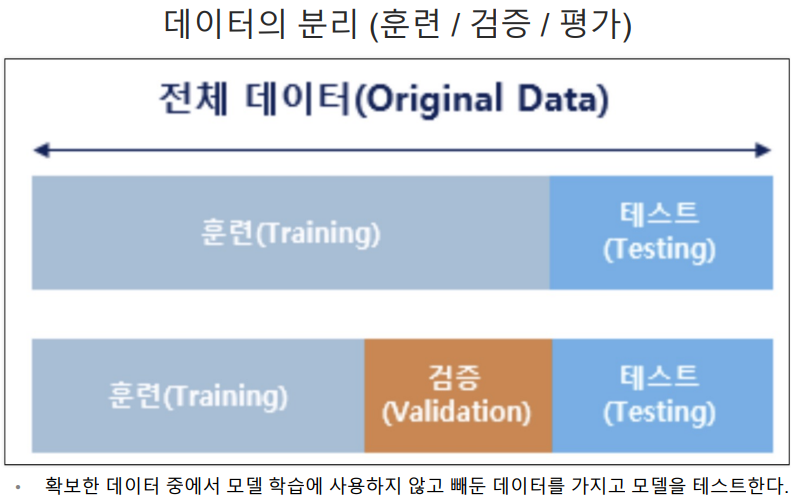
데이터 나누기

데이터 자체를 구하기 어려운 경우도 많아 내가 만든 모델이 과적합인지 아닌지 판단하기 어려운 경우도 있다. 그렇기에 모델을 만들기 전에 현재 가지고 있는 데이터 중 테스트용 데이터를 미리 나눠놔야 한다.

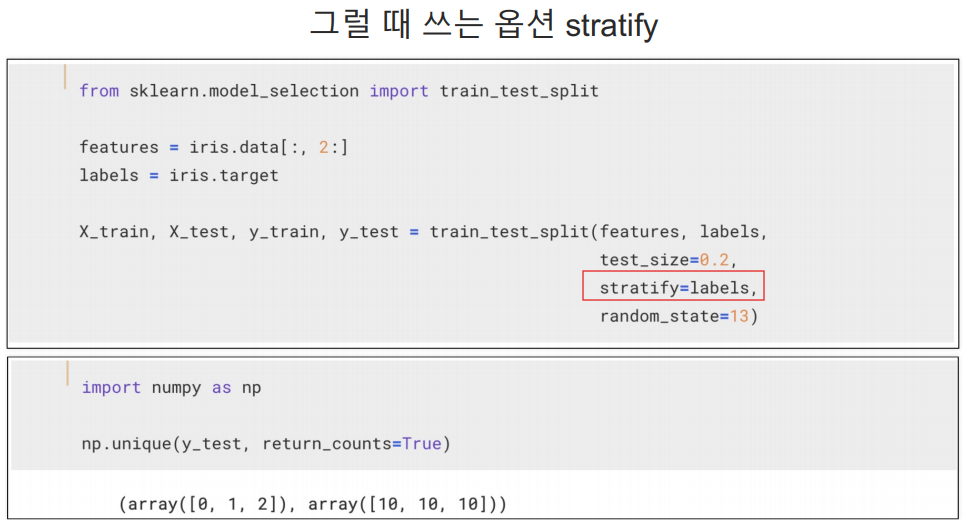
입력 데이터(독립 변수): features에 있는 값을 사용
타깃 레이블(종속 변수): labels 값
test_size = 0.2 : 전체 데이터의 20%가 테스트 데이터
random_state: 난수 시드를 설정하여 데이터를 무작위로 분할하는 과정을 재현 가능하게 한다.

구성요소는 [0, 1, 2]가 있다.
0이 9개, 1이 8개 2가 13개이다. 꼭 모두 동일한 개수일 필요는 없다. 그건 본인 판단이다. 하지만 클래스별 분포를 모두 동일하게 하려면 'stratify'를 사용하면 된다.

max_depth가 깊을수록 내가 제공한 데이터에 점점 더 100% 일치한다. 하지만 나의 데이터에 너무 최적화되면 모델의 성능이 좋지 않으니 max_depth를 조정해서 성능을 제한하고 규제하는 것이다.

훈련용 데이터에 대한 accuracy 확인

모델 확인

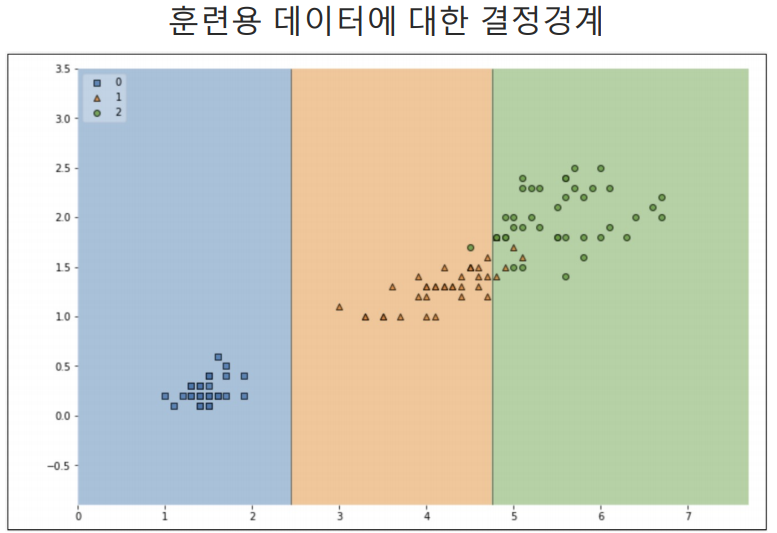
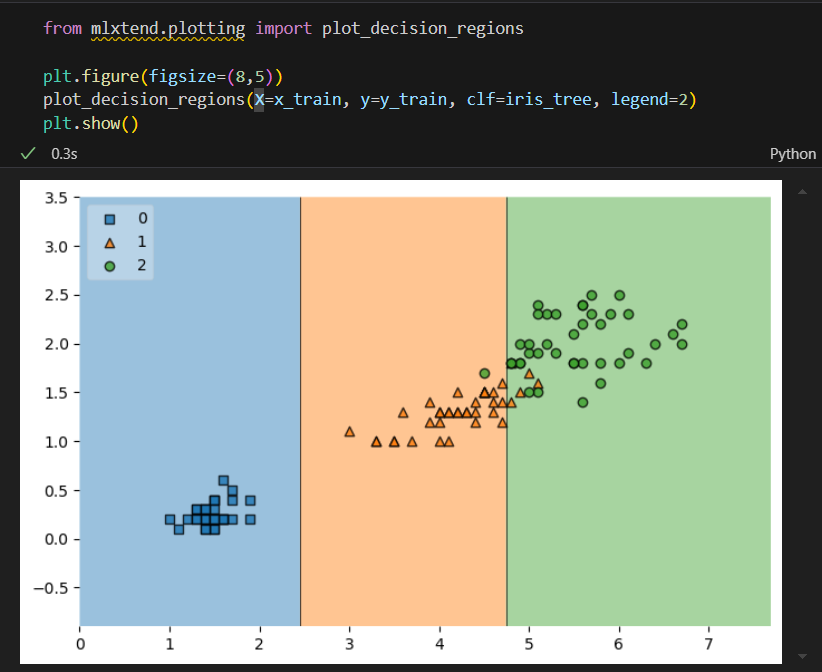
결정경계 확인

훈련용 데이터에 대한 accuracy가 0.95 였는데 테스트 데이터는 0.96으로 그 주변에 있으니 과적합은 아니구나 판단.

150개의 전체 데이터를 가지고 train 데이터와 test 데이터로 분리시켜서 강조하고 결정경계까지 넣는 과정
alpha: 하이라이트 정도

모델을 사용하는 방법

테스트 데이터를 내가 만든 모델(iris_tree)에 넣고 예측을 시킨다.

여기서 [[4.3, 2., 1.2, 1.0]] 처럼 대괄호[]를 두번 쓰는 이유는 행렬로 만들어주기 위함이다. 행렬로 만들어줘야 해당 데이터를 적용해 계산할 수 있다.
단순히 대괄호 한번만 사용하면 1행 4열이 아니라 4개만 있는 리스트 형태가 된다.
위 결과 array에 있는 내용을 보면 versicolor일 확률이 97%로 나온다.

petal length가 0.42, petal width가 0.57의 중요도를 가진다.

zip

zip은 여러 요소들을 묶어 튜플로 만들어주는 함수다.

pairs = [('a', 1), ('b', 2), ('c', 3)]가 주어졌을 때 *pairs는 이를 개별 요소로 풀어준다. 즉, ('a', 1), ('b', 2), ('c', 3)으로 변환된다.
즉, zip(('a',1), ('b',2), ('c',3))이되어 'a', 'b', 'c'끼리 하나의 튜플로 묶이고 1, 2, 3 끼리 하나의 튜플로 묶인다.