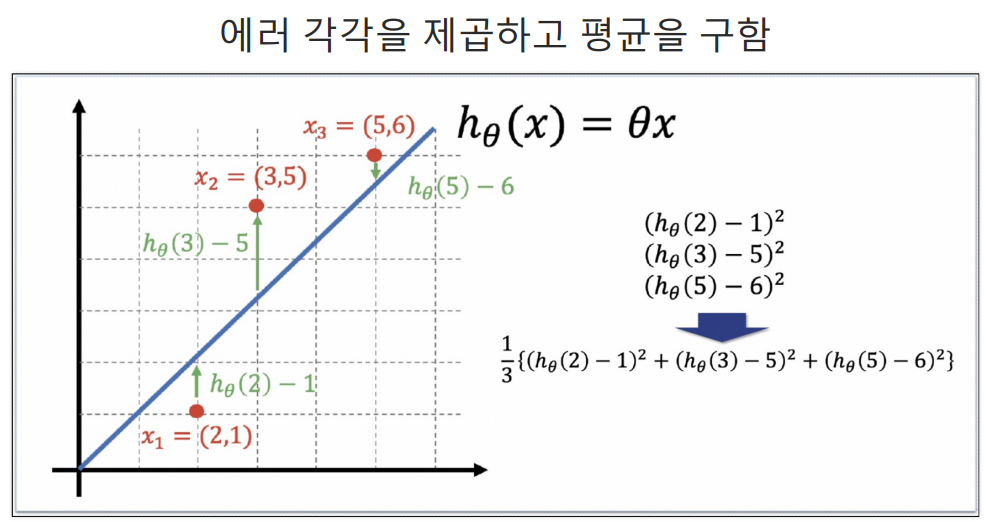

h는 예측값이다.
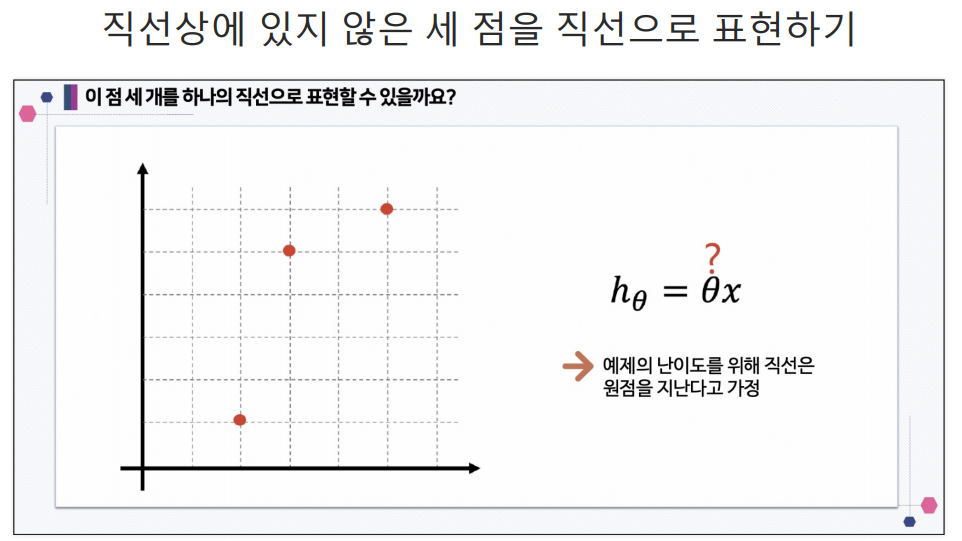
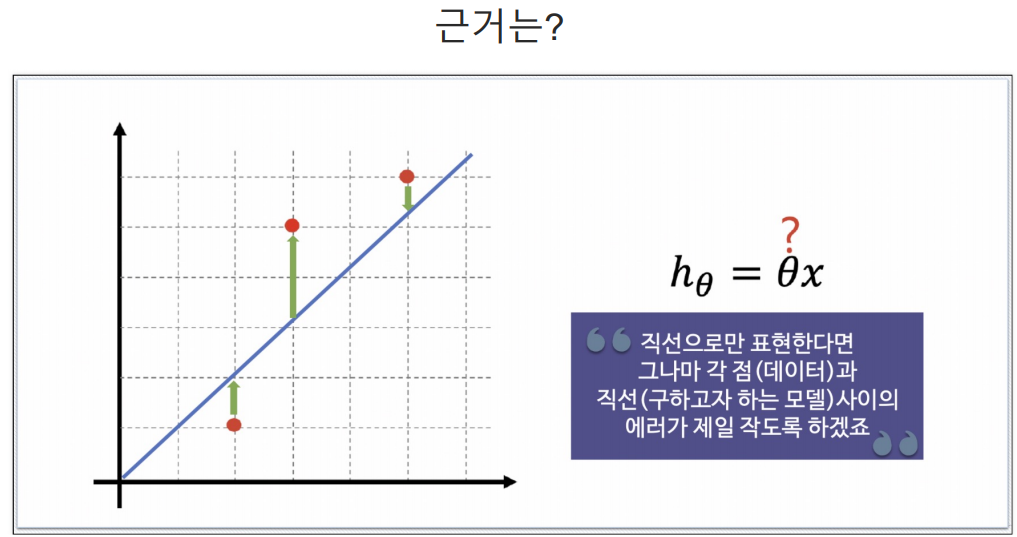
Hypothesis 함수
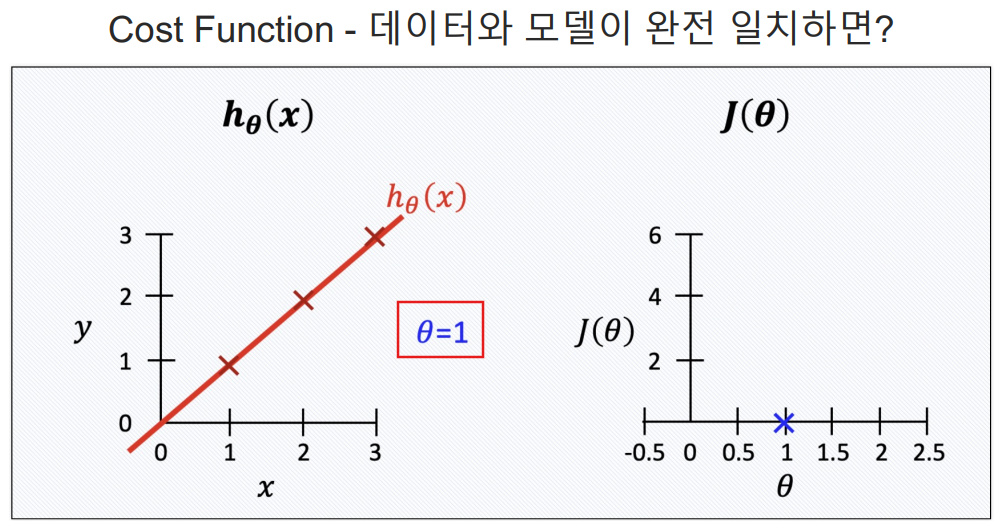
Cost Function
- 딥러닝에서도 많이 사용함.
- cost function은 에러를표현하는 도구임.
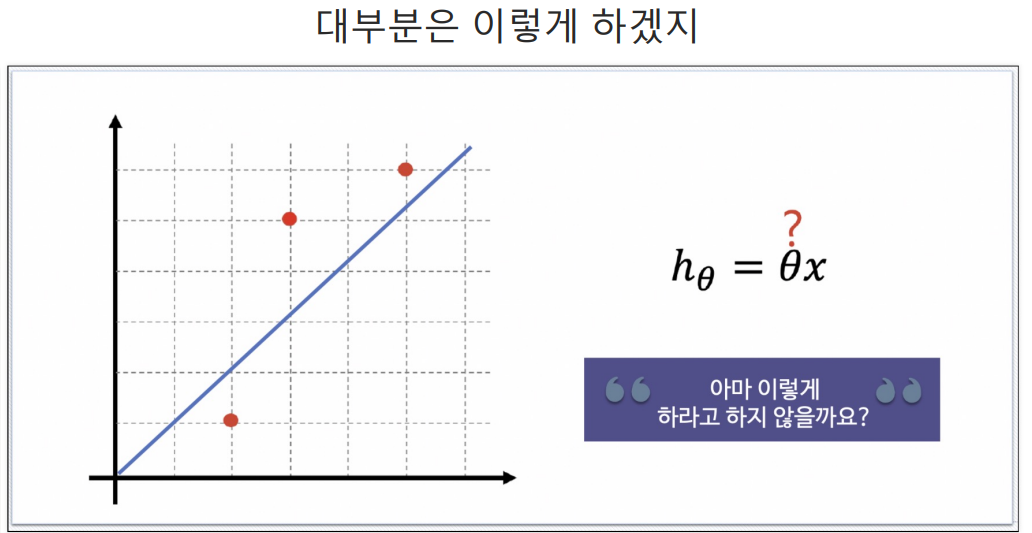
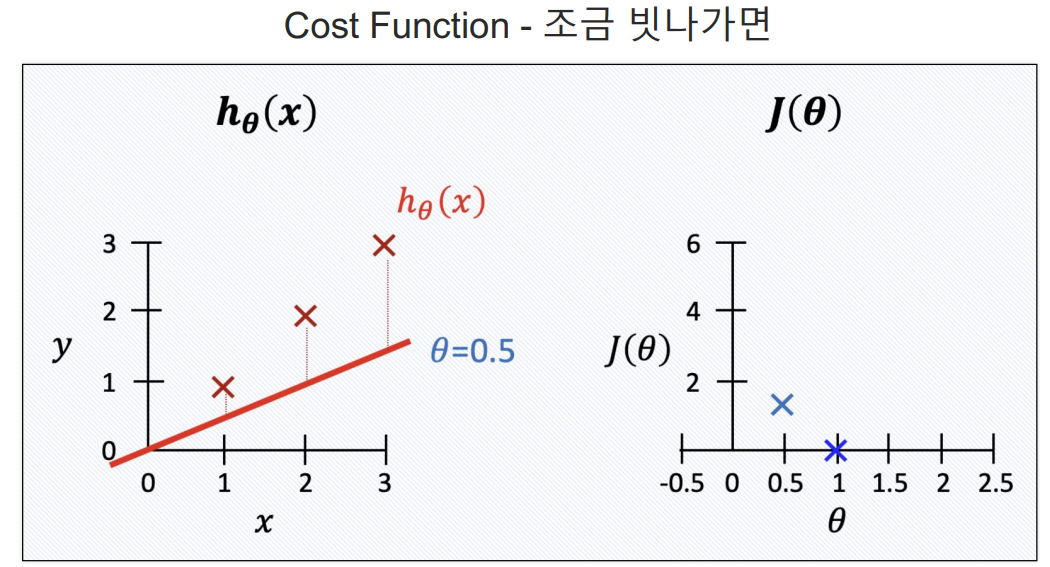
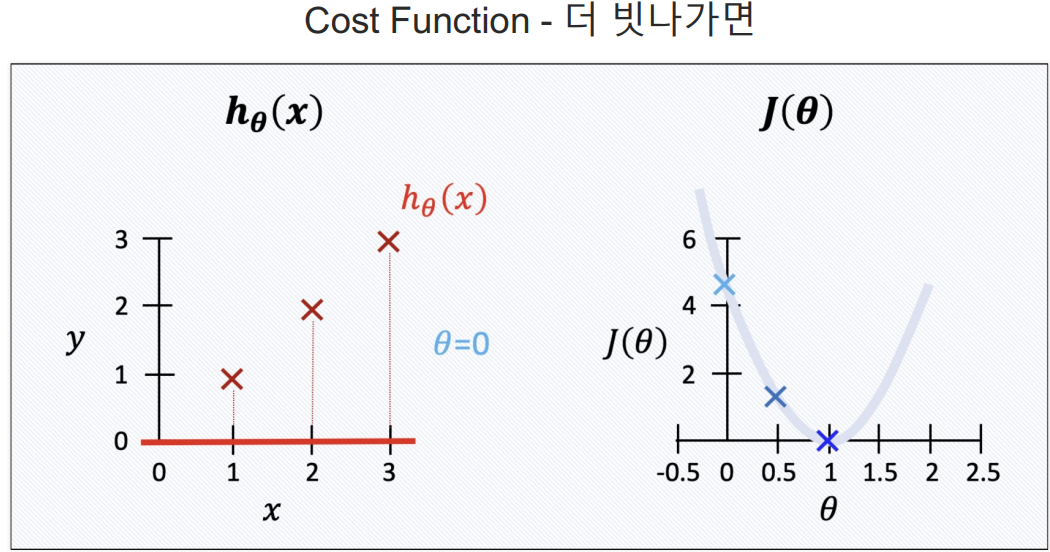
- 에러가 작을수록 좋으니까 cost function을 최소화 할 수 있는 기울기가 최적의 직선이다.


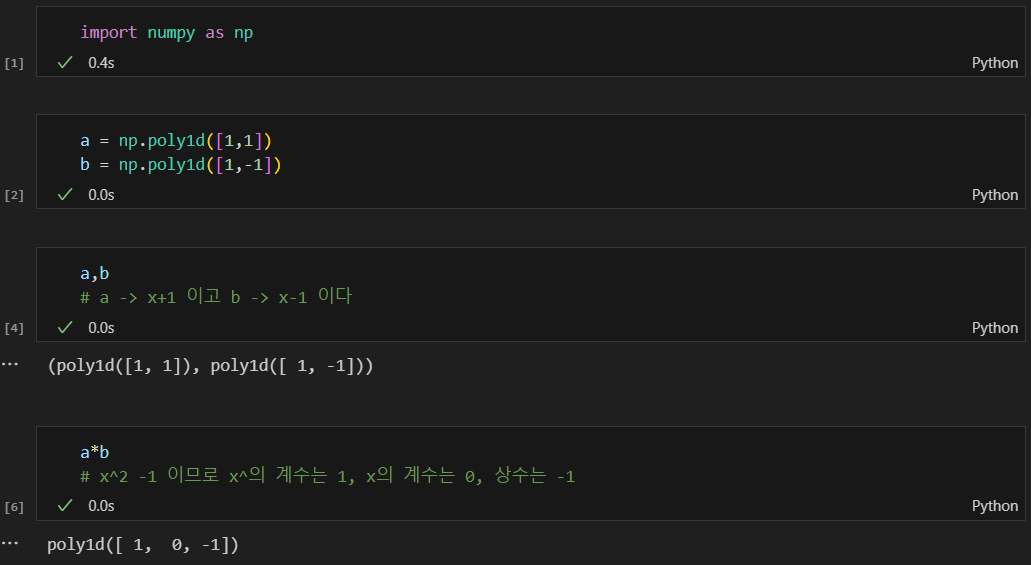

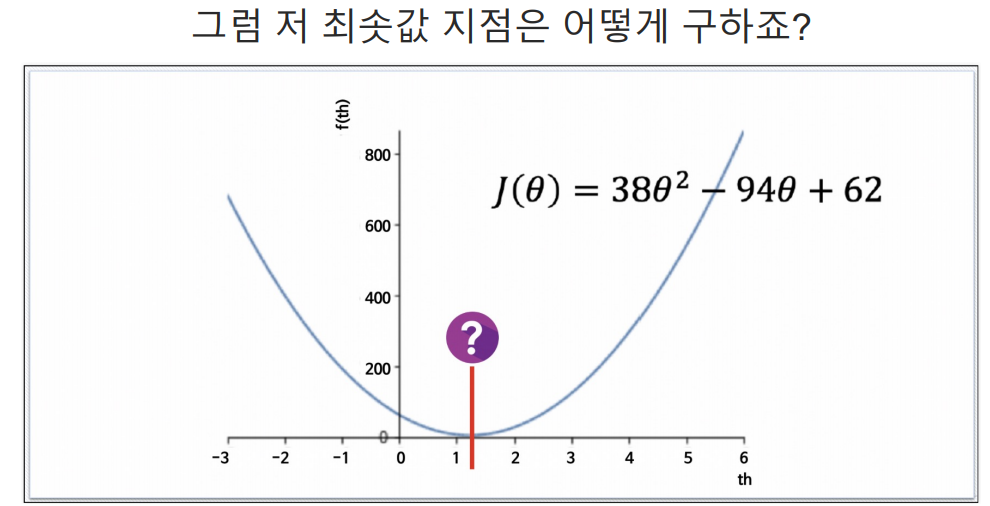


sympy를 이용해 cost function 최소값 구하기
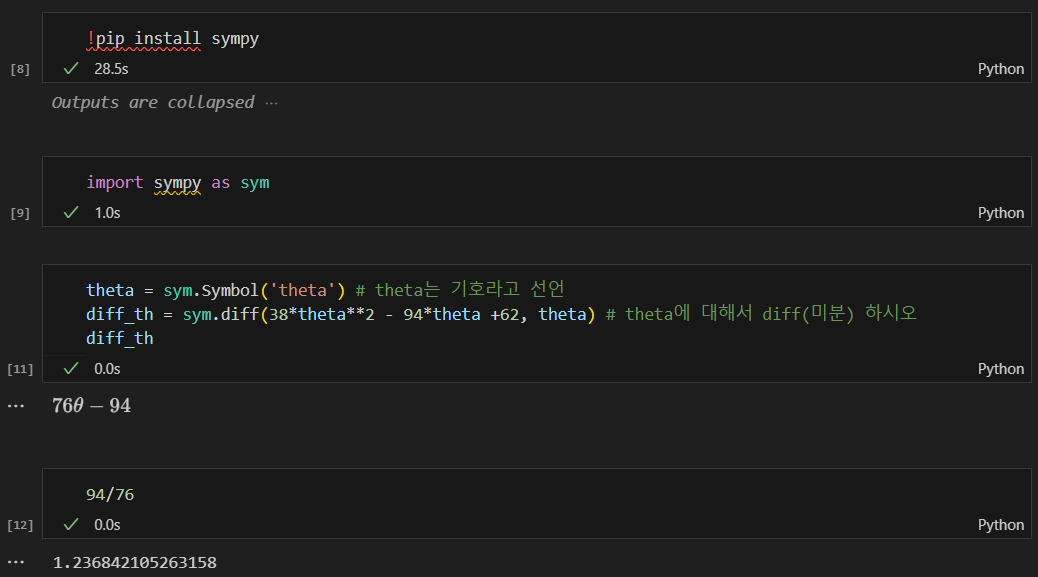
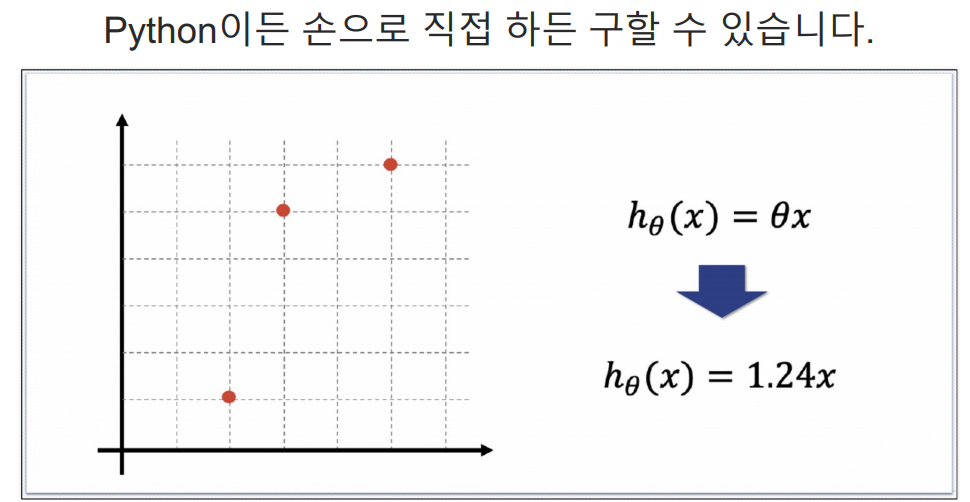
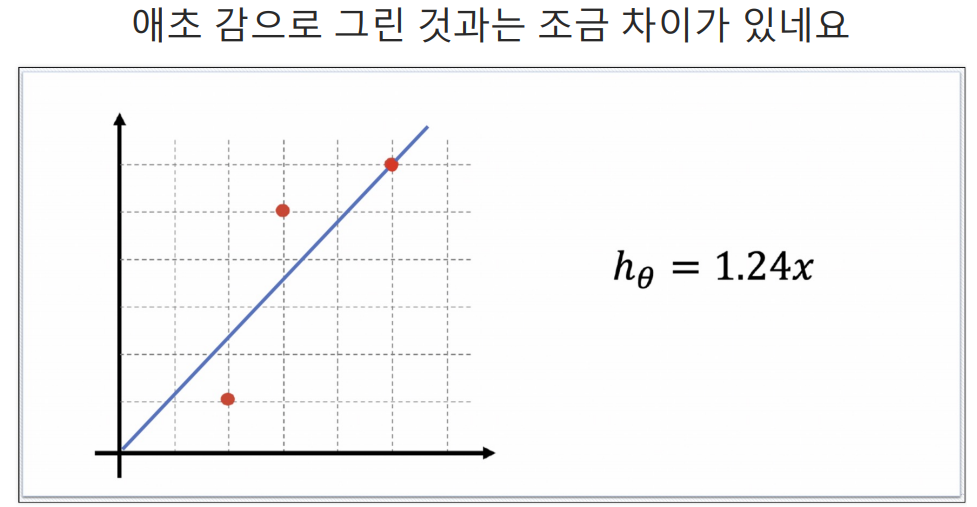
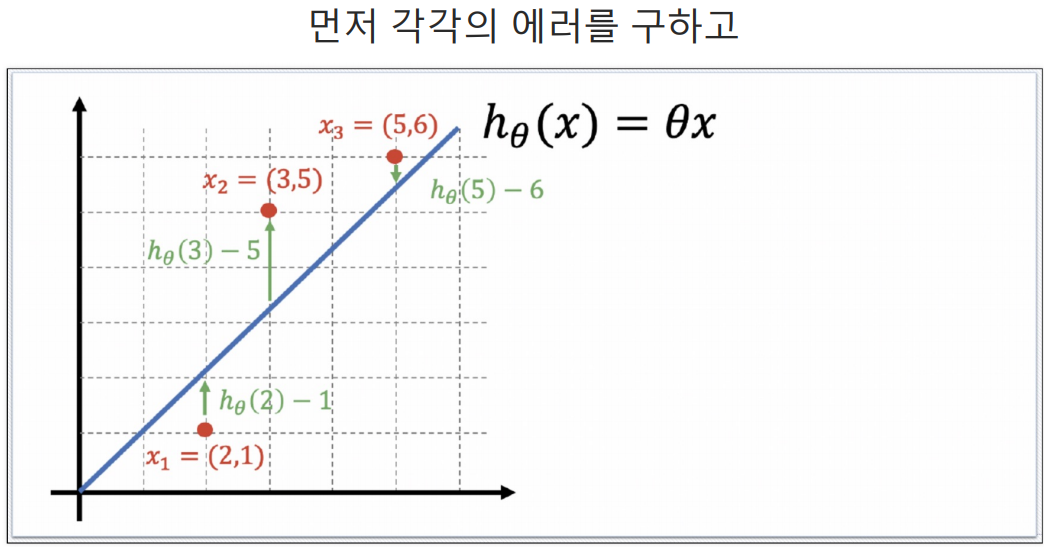
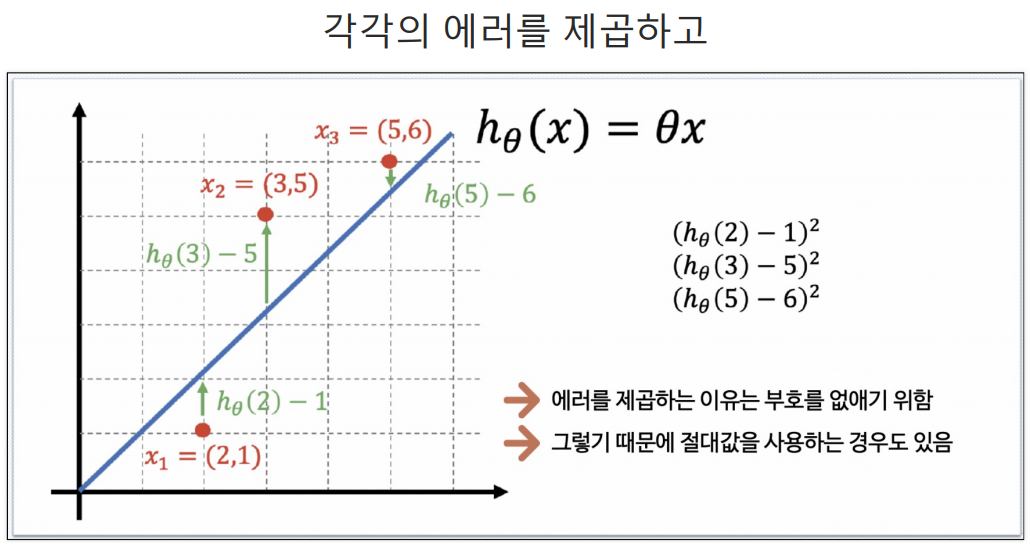
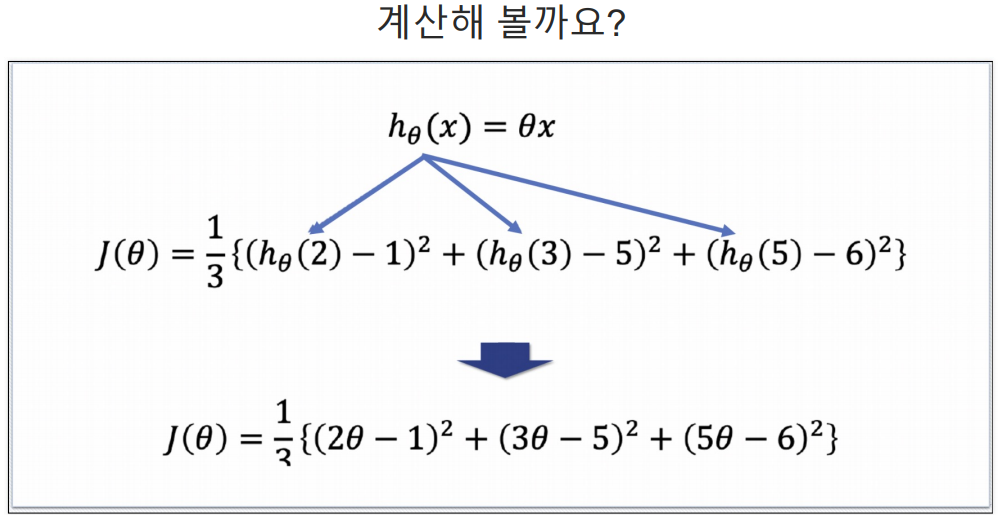
예측하기 위한 직선(h(x) = Θx)을 기준으로 에러(예측값과 실제 값의 차이를 제곱해서 더한값들)가 최소가 되게하는 값을 구하면 Θ 값을 구할 수 있다. 여기서 구한 Θ값이 결국 가장 에러가 적은 기울기가되는 것이다.
Gradient Descent
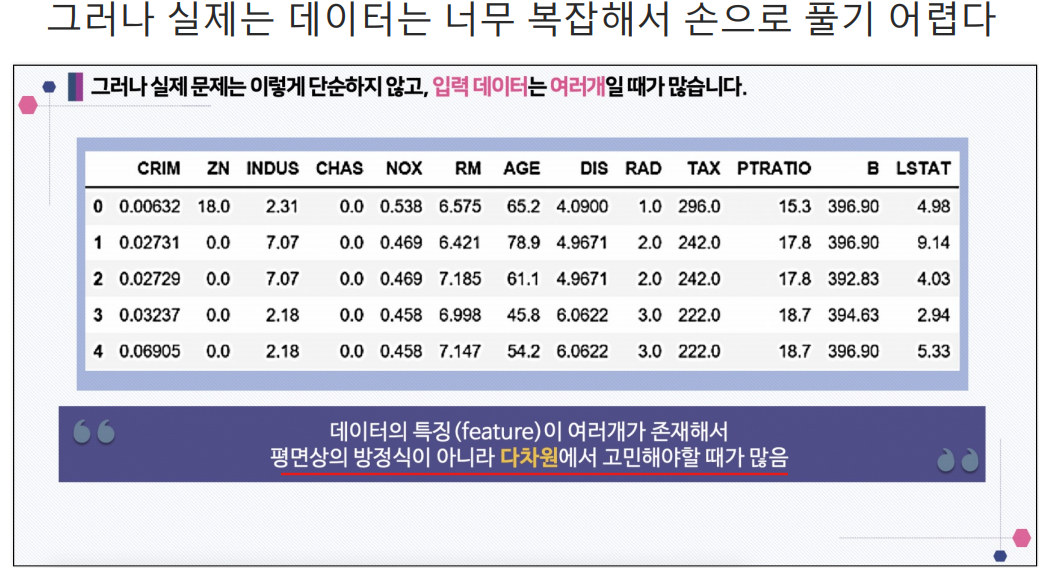
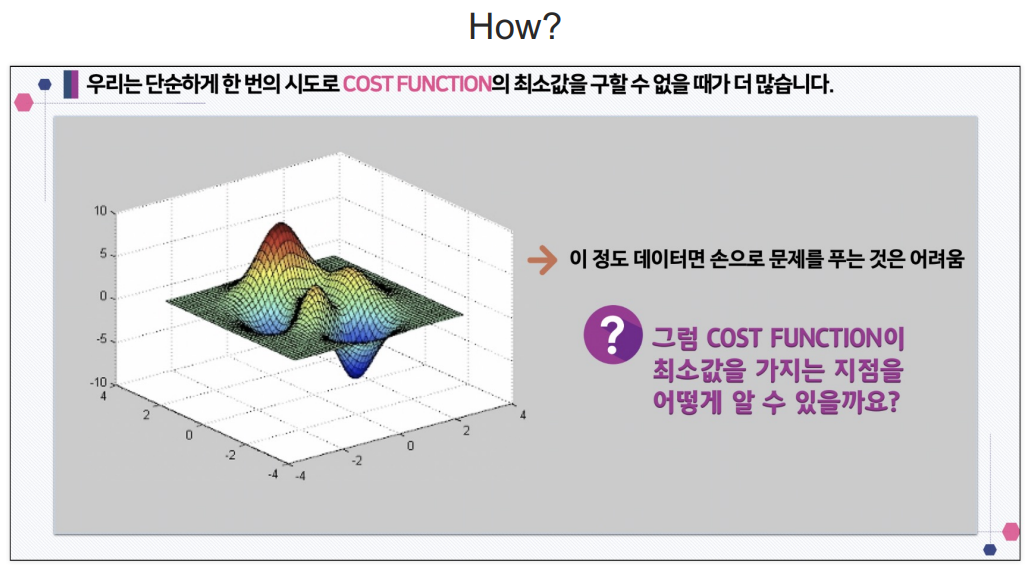
- 다차원의 데이터일때는 위의 방법으로 cost function을 찾는것이 어려움. 그래서 이 방법을 사용함.
- 요즘에 이 방법을 사용하지는 않음.
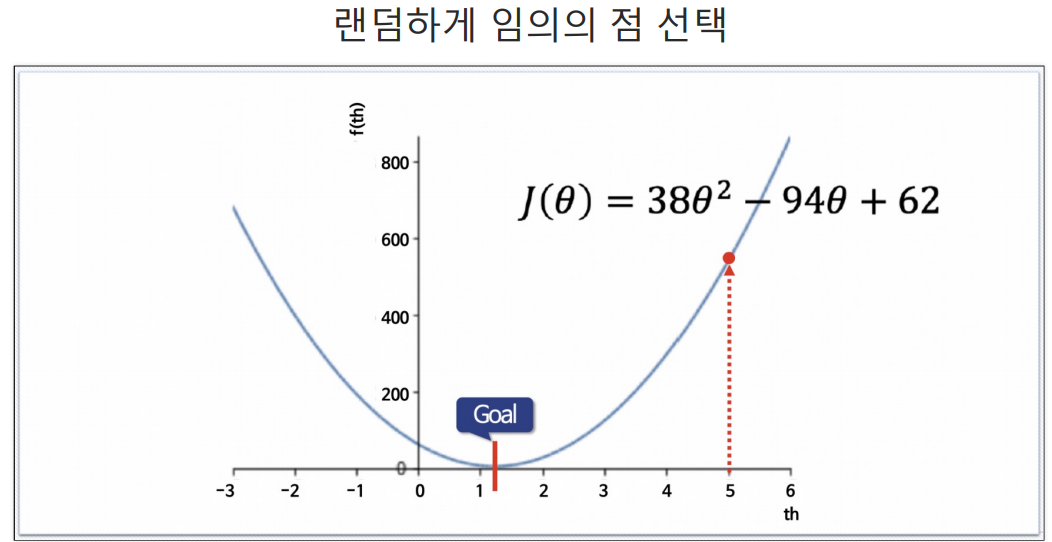
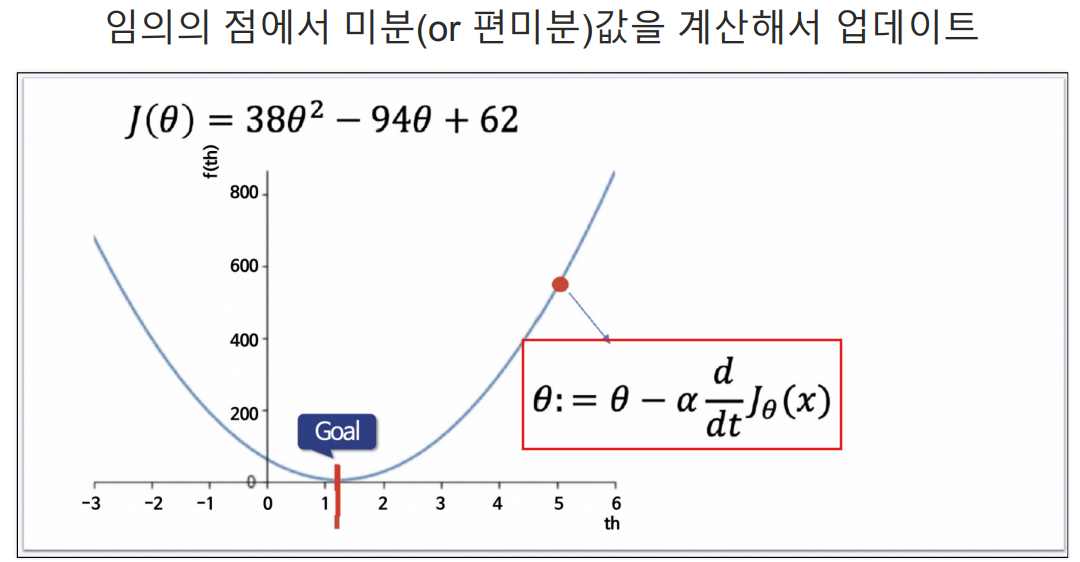
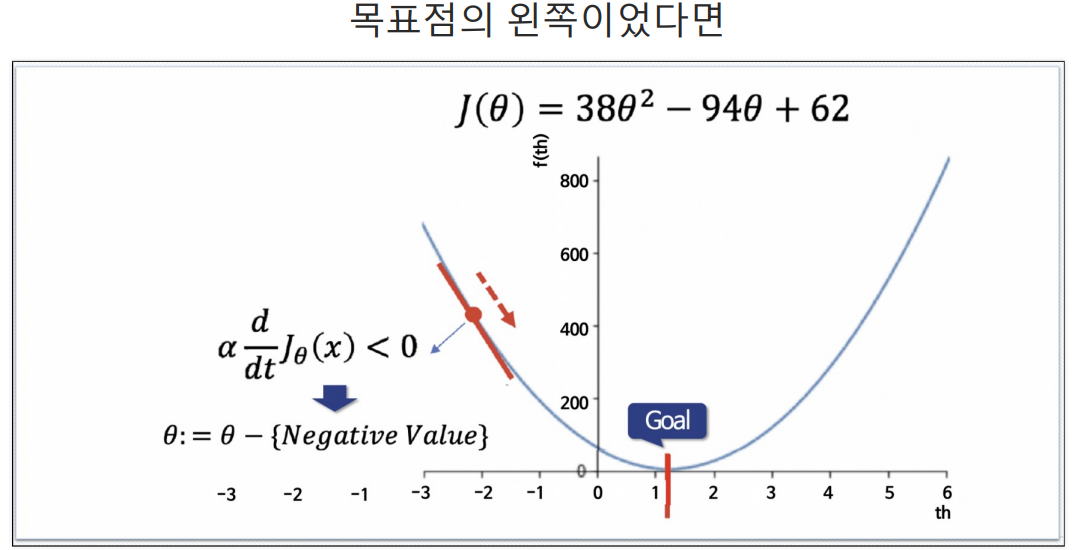
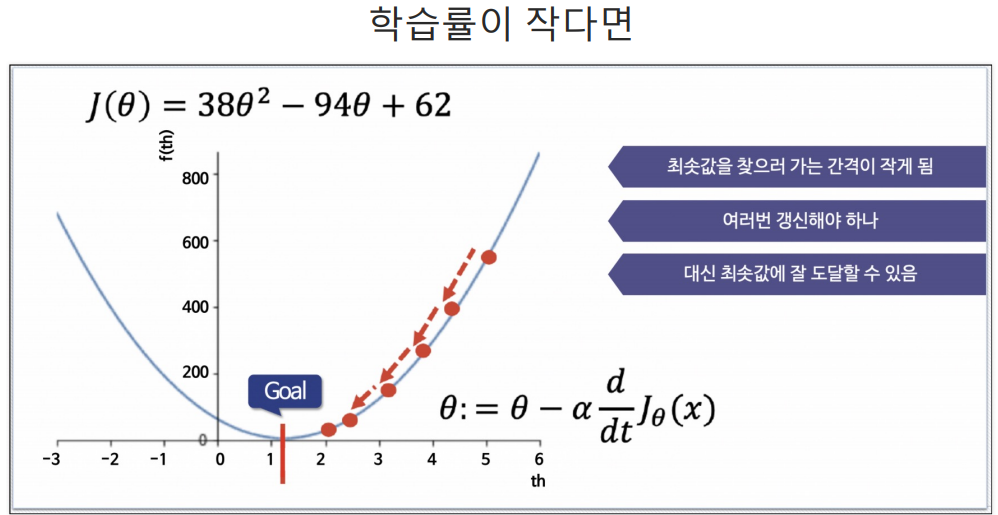
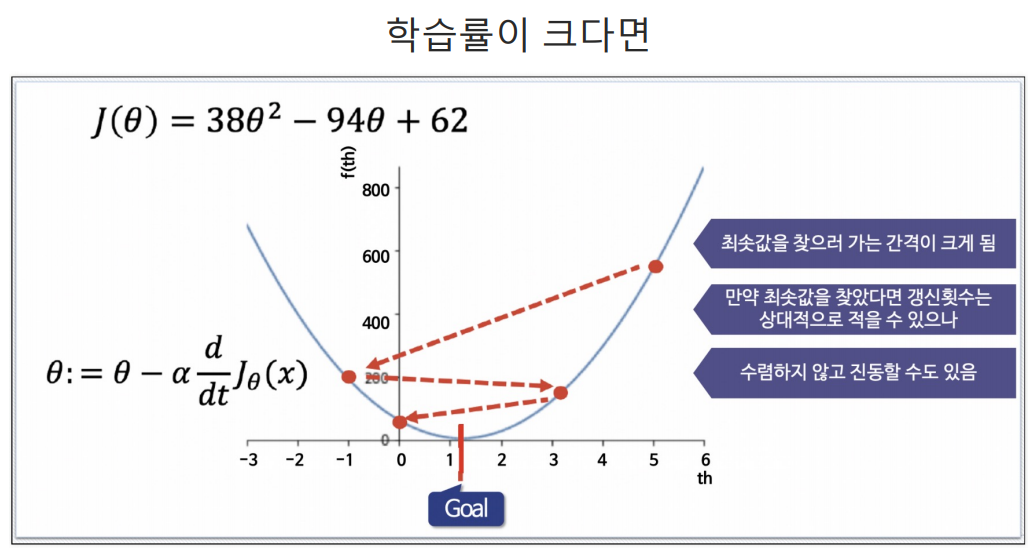
임의의 점이 오른쪽이든 왼쪽이든 (임의의 점 - 임의의 점에서의 기울기)를 하게되면 점점 목표 Θ값으로 가까워짐. 이것이 Gradient Descent.

α는 학습률(Learning Rate)이다.
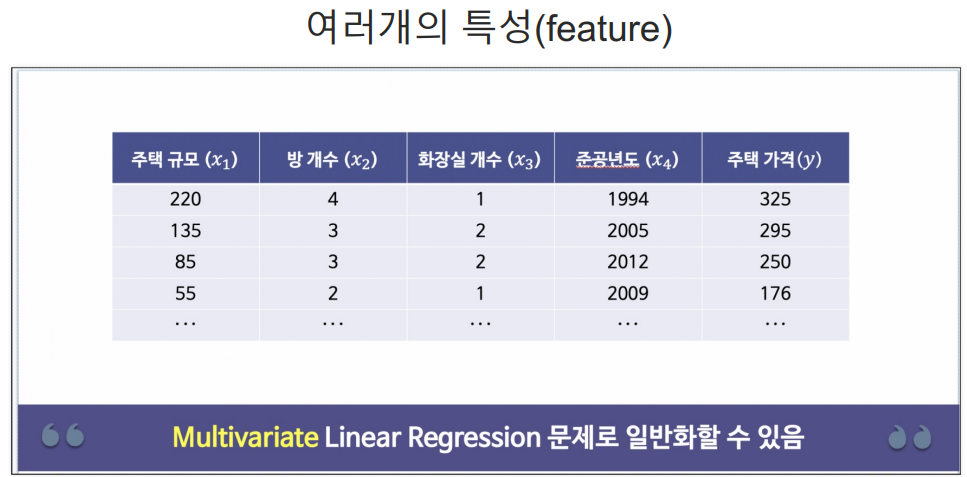
다변수 데이터에 대한 회귀

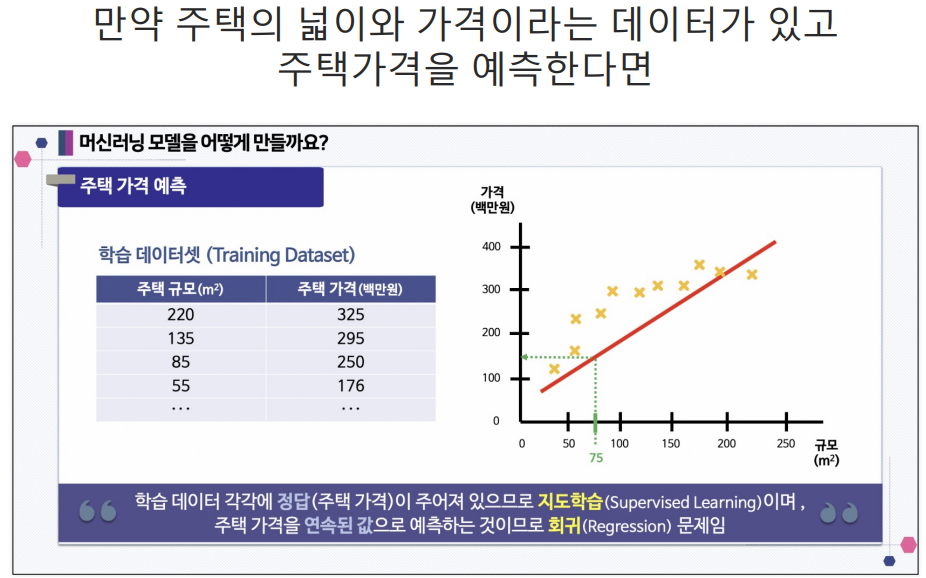
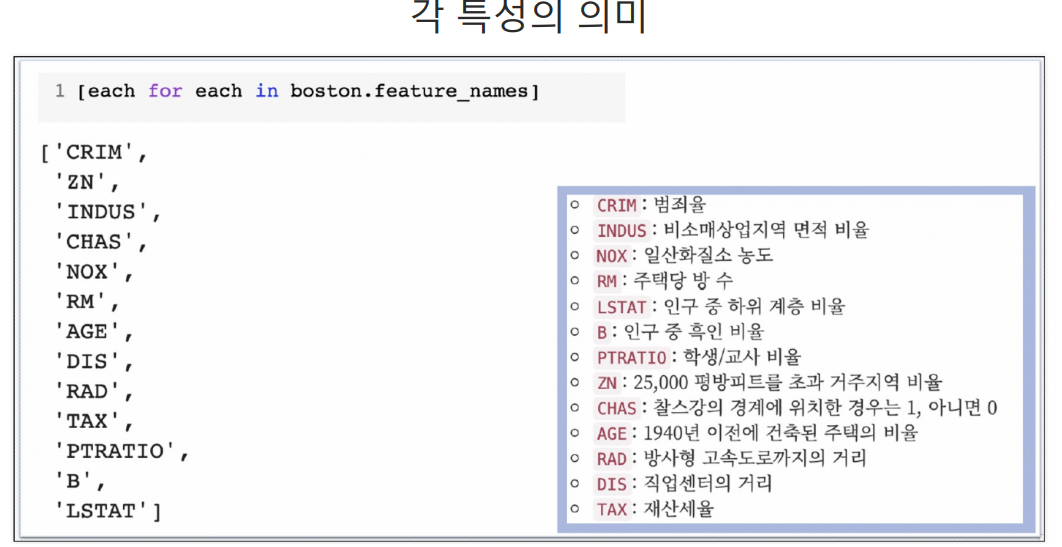
Boston 집값 예측
from sklearn.datasets import load_boston 의 데이터는 더이상 제공되지 않음.
그래서 그냥 캡처이미지와 강의로 학습.

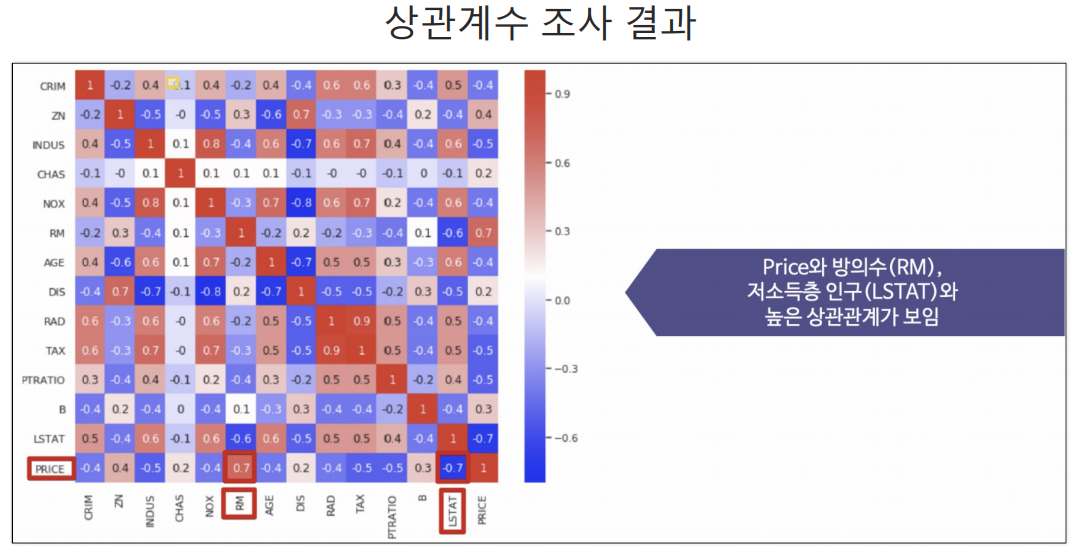
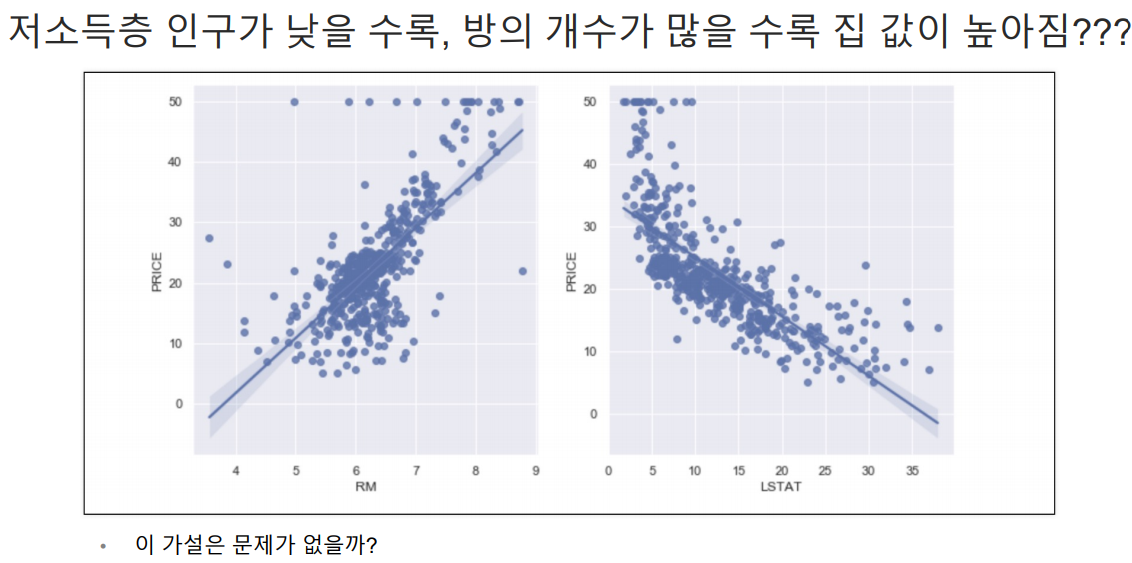
LSTAT와 PRICE의 관계 파악


LinearRegression은 OLS랑 같은거다.

회귀는 분류처럼 정확성을 보는 accuracy_score가 없다.
많이 사용하는 것이 mean_squared_error이다.
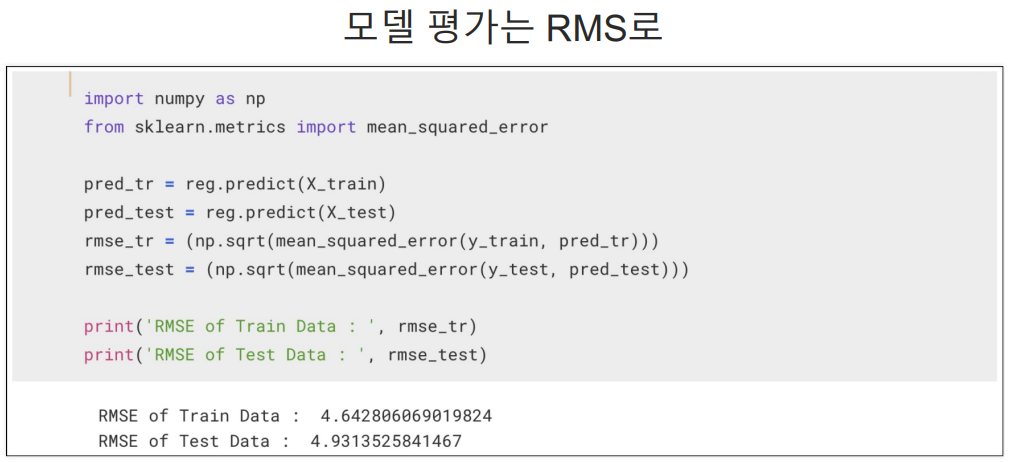

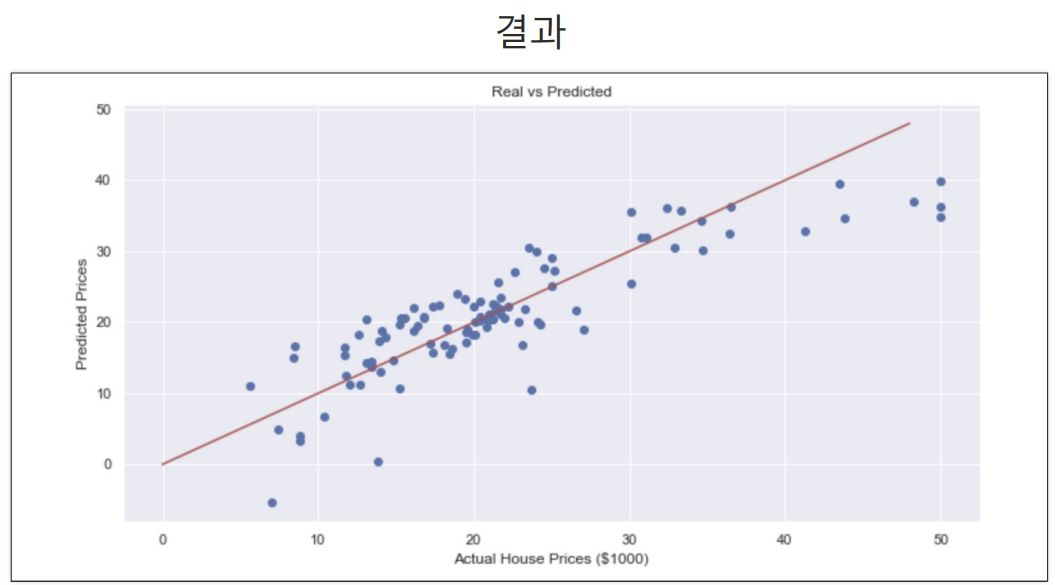
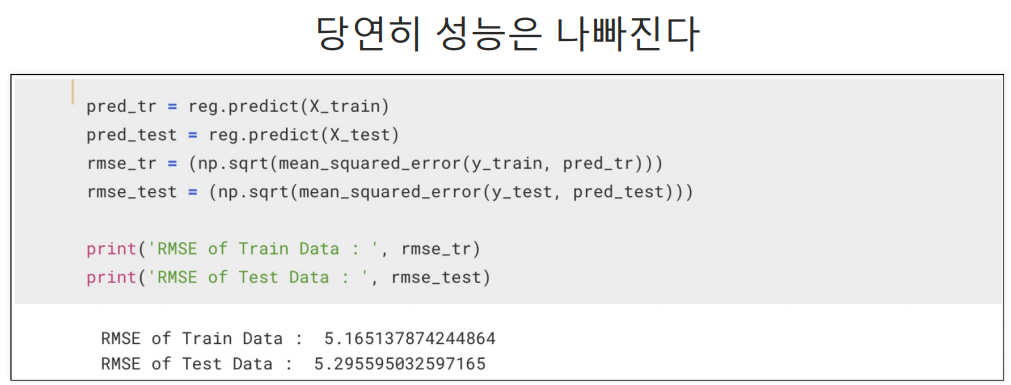
인구중 하위계층비율인 LSTAT 데이터를 제외하고 모델을 테스트 해봄.

당연히 성능은 나빠지지만 그렇다고 LSTAT 데이터를 넣어야할지 고민할 필요는 있는 것이다.(하위계층이 살고있으니까 어찌보면 다연히 집값이 그곳이 싼 것이기에 이 데이터를 포함해 boston의 집값을 예측하기는 무리가 있긴함.)