PCA(Principal Component Analysis)
주성분 분석
- 차원축소와 변수추출 기법으로 널리 쓰이고 있다.
- 많은 특성(변수)을 가진 데이터는 시각화나 분석하기 어려울 수 있어 고차원의 데이터를 낮은 차원의 데이터로 바꿔 시각화나 모델링에 용이하게 하는 것.
- feature(변수)를 추출하는 것이 아니라 새로운 feature를 만드는 것이다.
- pca를 하기위해서는 데이터를 정규화 하는것이 필수다. 그렇지 않으면 스케일이 큰 특성이 주성분에 과하게 영향을 끼친다.
- 각 주성분을 표현하는 벡터는 원본데이터의 특성에 대한 가중치를 포함하고 있다.
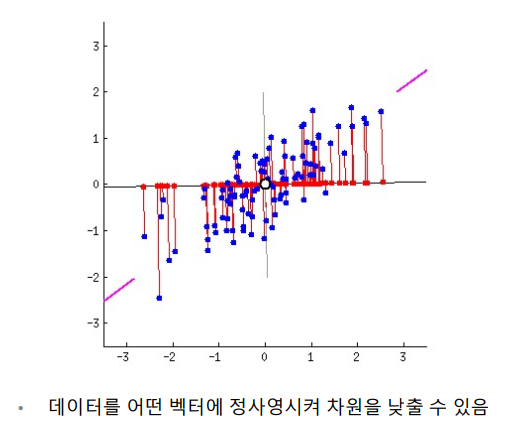
- 만약 n차원의 데이터를 2차원으로 줄인다면 주성분 벡터 2개의 값을 가지고 표현하는 것이다.


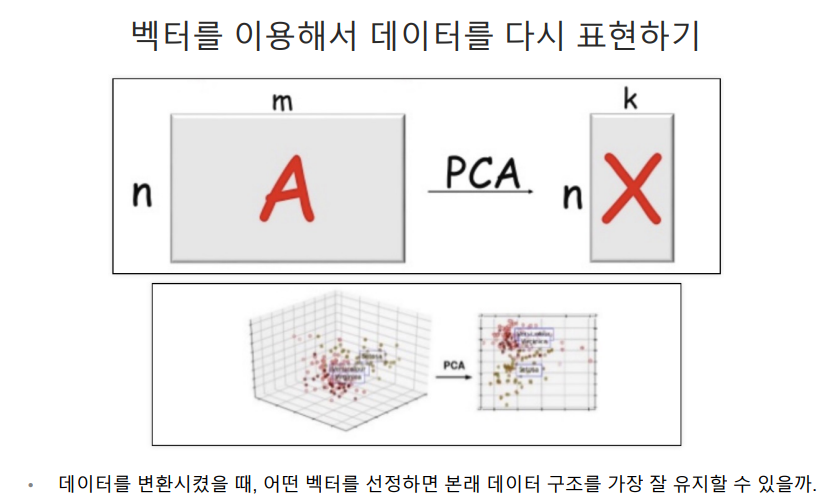
실습
np.random.RandomState(13)
- RandomState는 13과 같은 시드를 설정할 수 있는데 동일한 시드를 사용하면 항상 동일한 난수를 만들 수 있다.
- 대신 매번 np.random.RandomState(13)이것도 같이 실행해 줘야함.
- 처음에만 rng=np.random.RandomState(13)로 해놓고 rng.rand(2,2)만 계속 실행하면 매번 다른 난수값이 나온다.
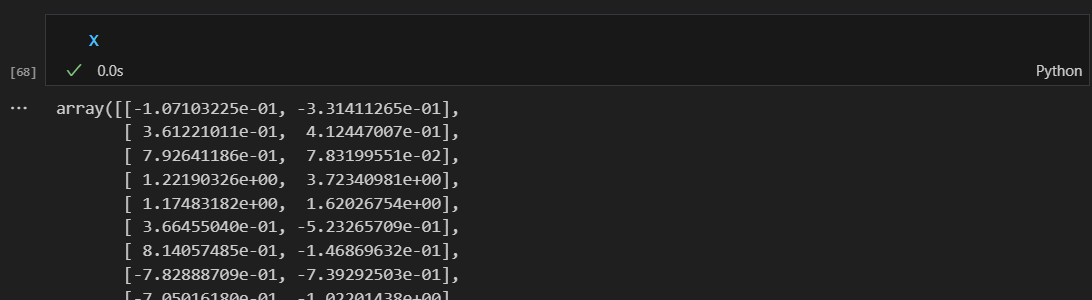
실습용 데이터
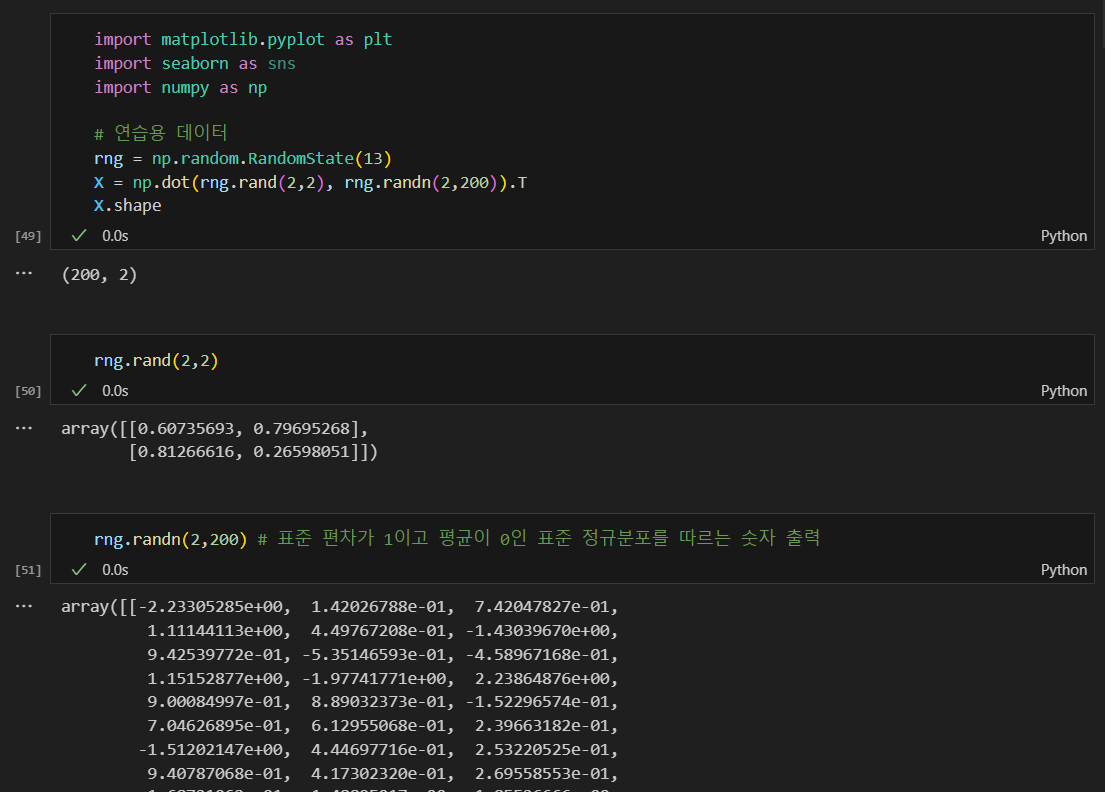
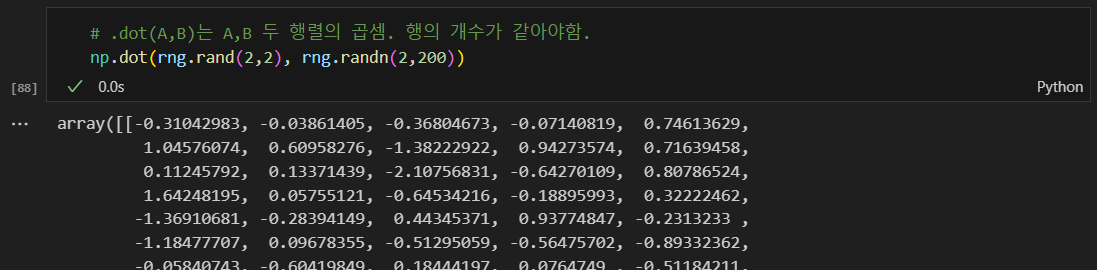
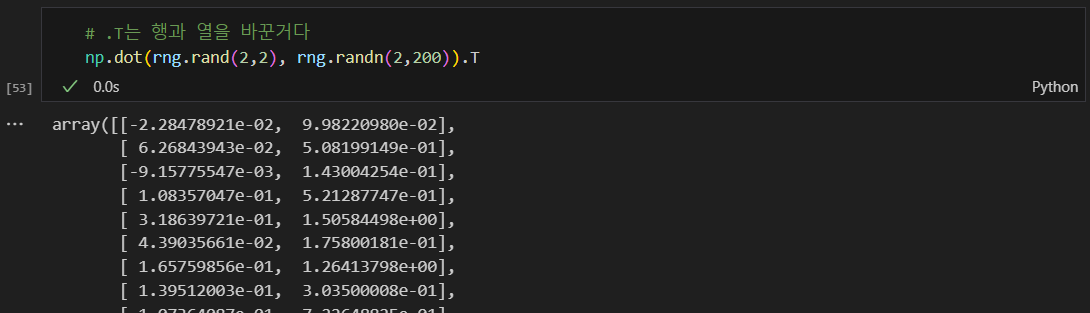
데이터 생긴거 확인
PCA 모델을 생성하고, 데이터 차원을 1로 축소 및 모델 학습
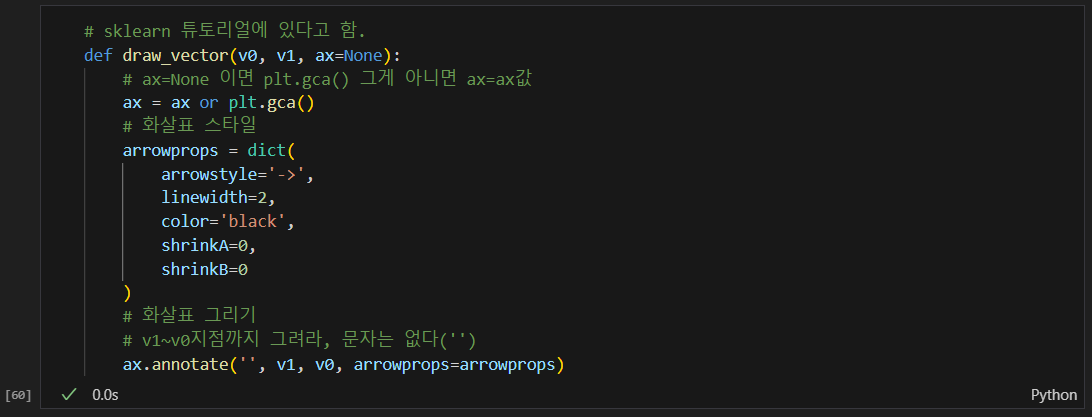
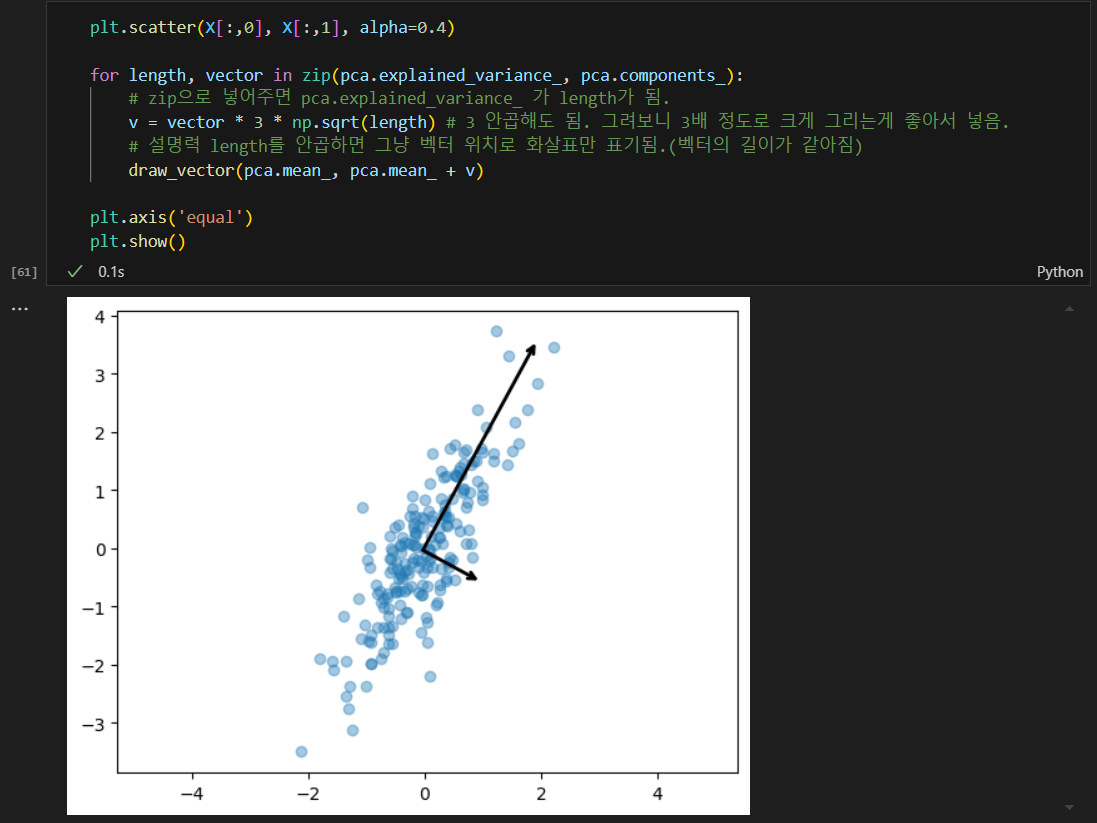
주성분 벡터 그릴 준비
주성분 벡터 그리기
데이터 차원을 1차원으로 축소
기존 테스트 데이터와 pca로 축소한 데이터 비교
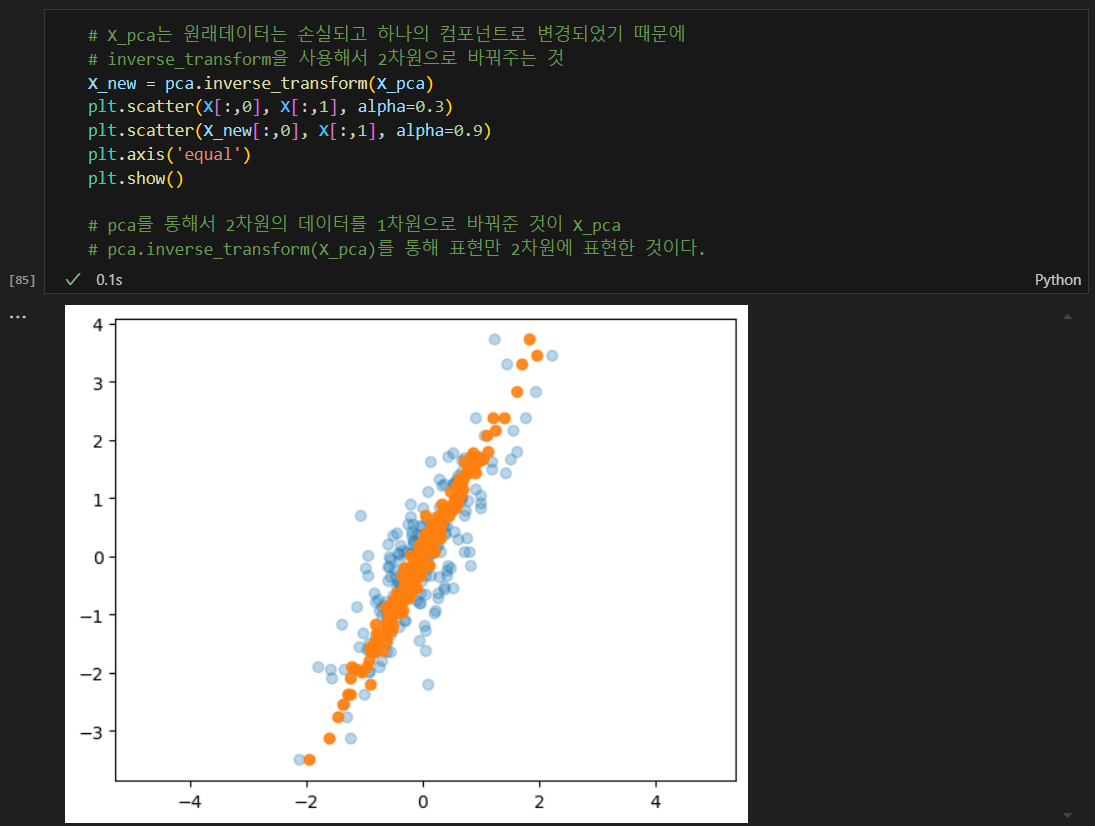
pca로 축소한 데이터를 2차원상에 그리기
iris 데이터로 pca 실습
iris 데이터 불러오기
pca를 위해 정규화
pca 결과를 리턴하는 함수 만들기
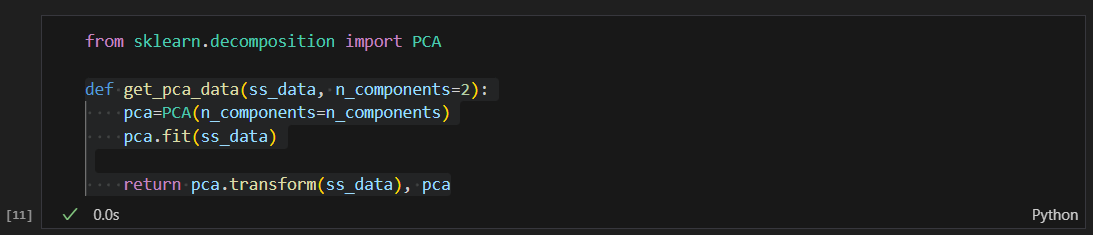
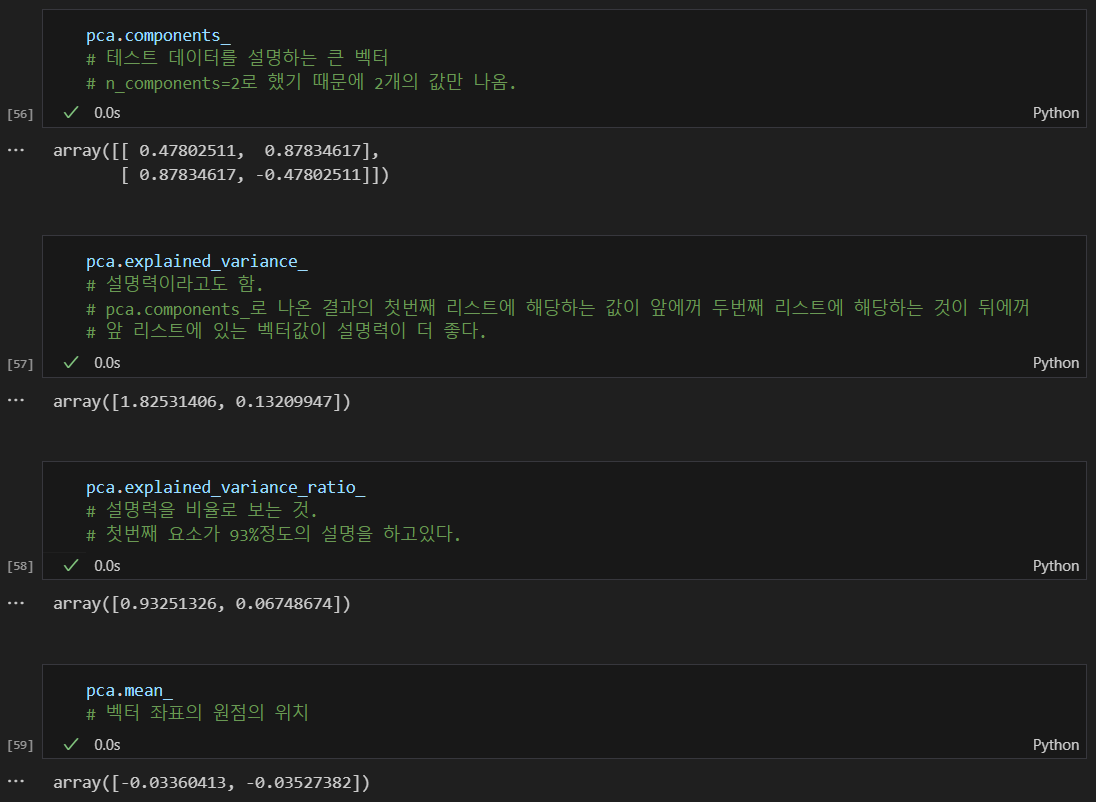
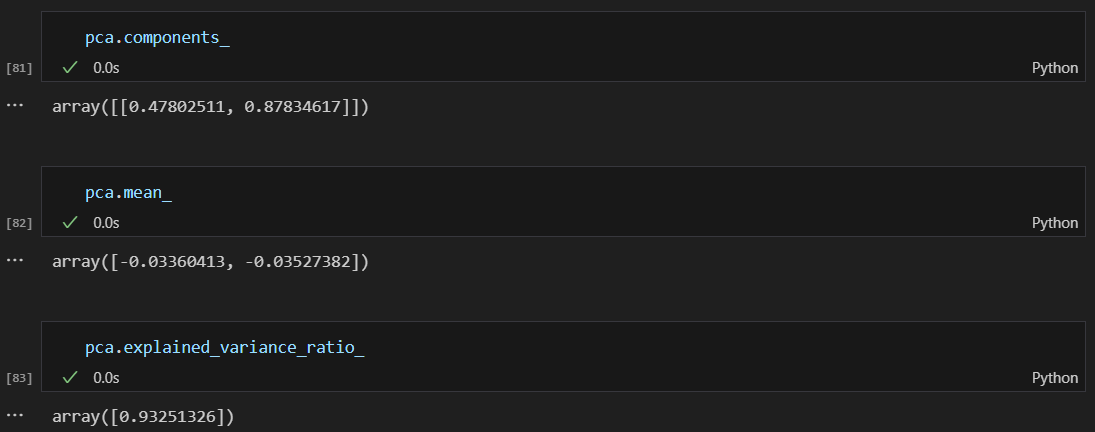
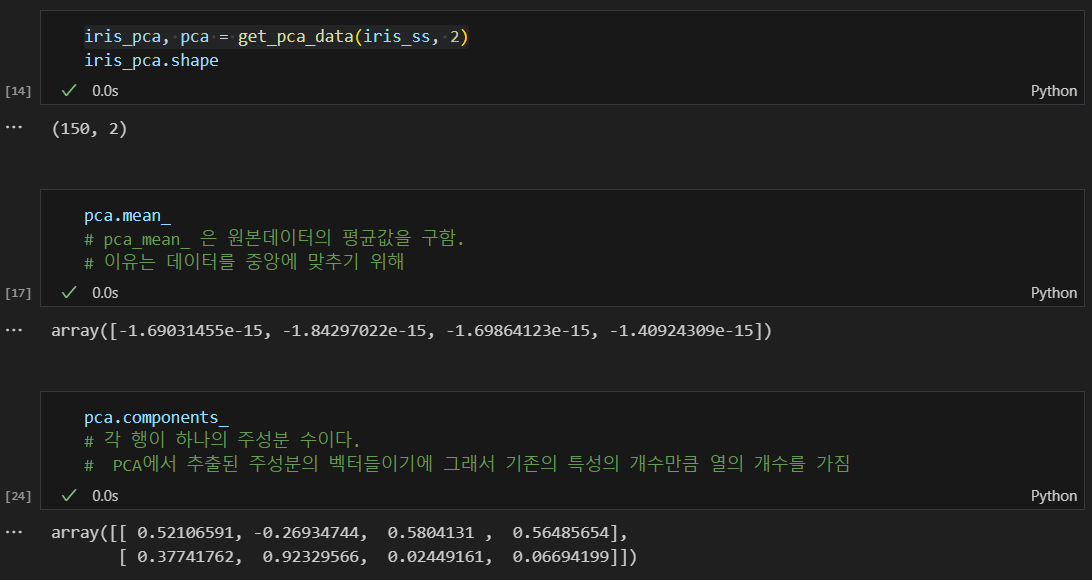
관련 pca 값 확인
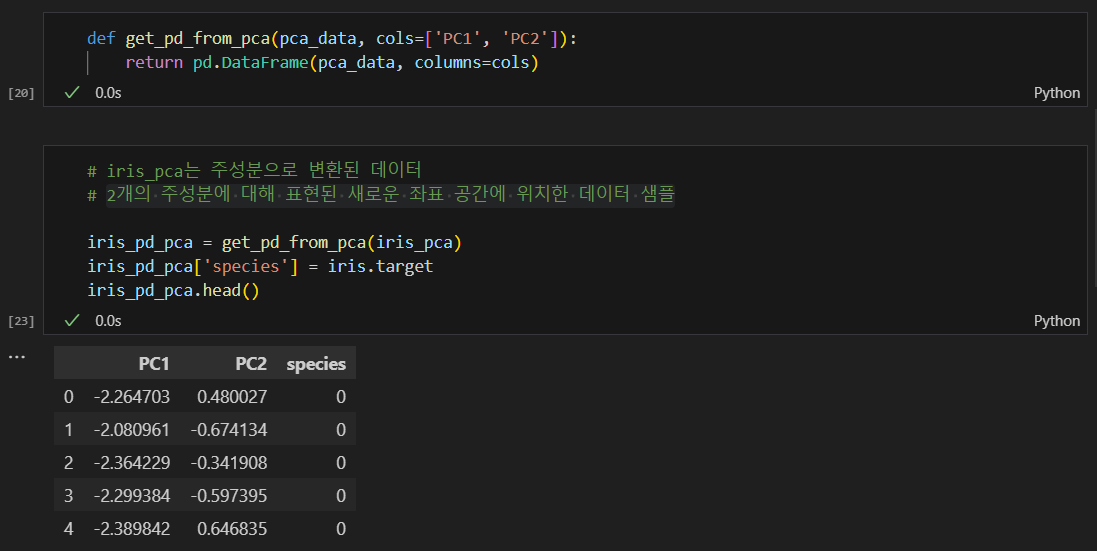
pca를 pandas로 정리
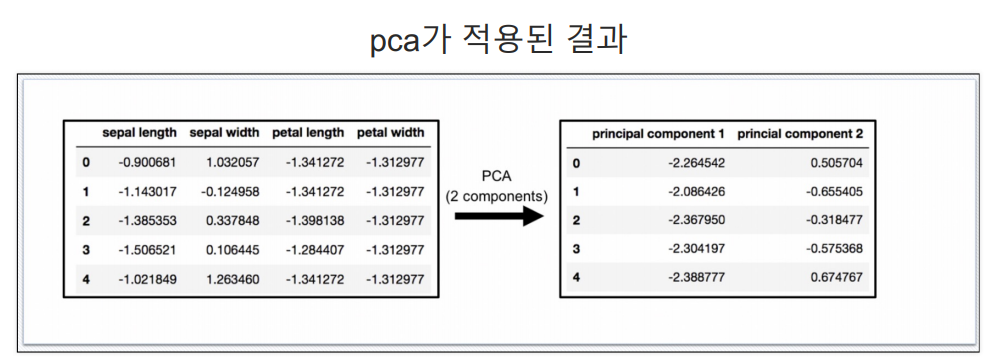
잠깐!
pca.components_와 iris_pca 데이터 형태가 왜 다른가?
- pca.components_는 각 행이 하나의 주성분이다.
- PCA에서 추출된 주성분의 벡터들이기에 그래서 기존의 특성의 개수만큼 열의 개수를 가짐
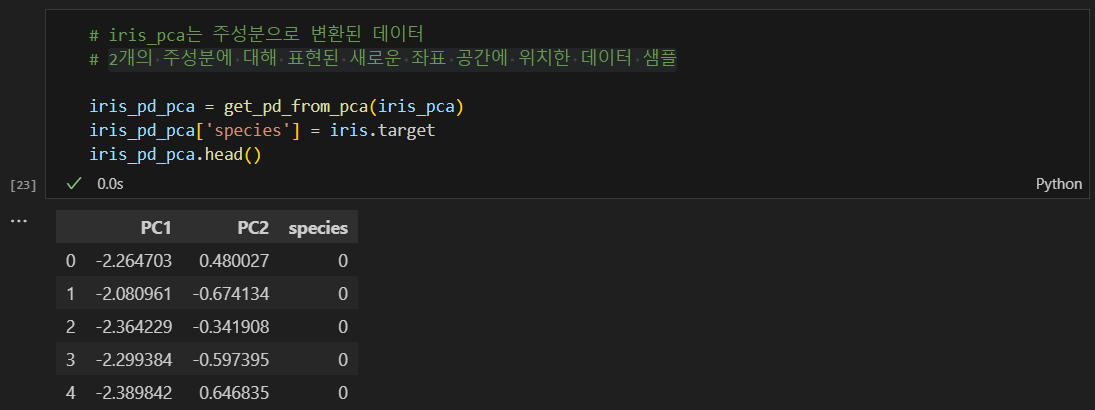
반면- iris_pca는 주성분으로 변환된 데이터이다.
- 2개의 주성분에 대해 표현된 새로운 좌표 공간에 위치한 데이터 샘플
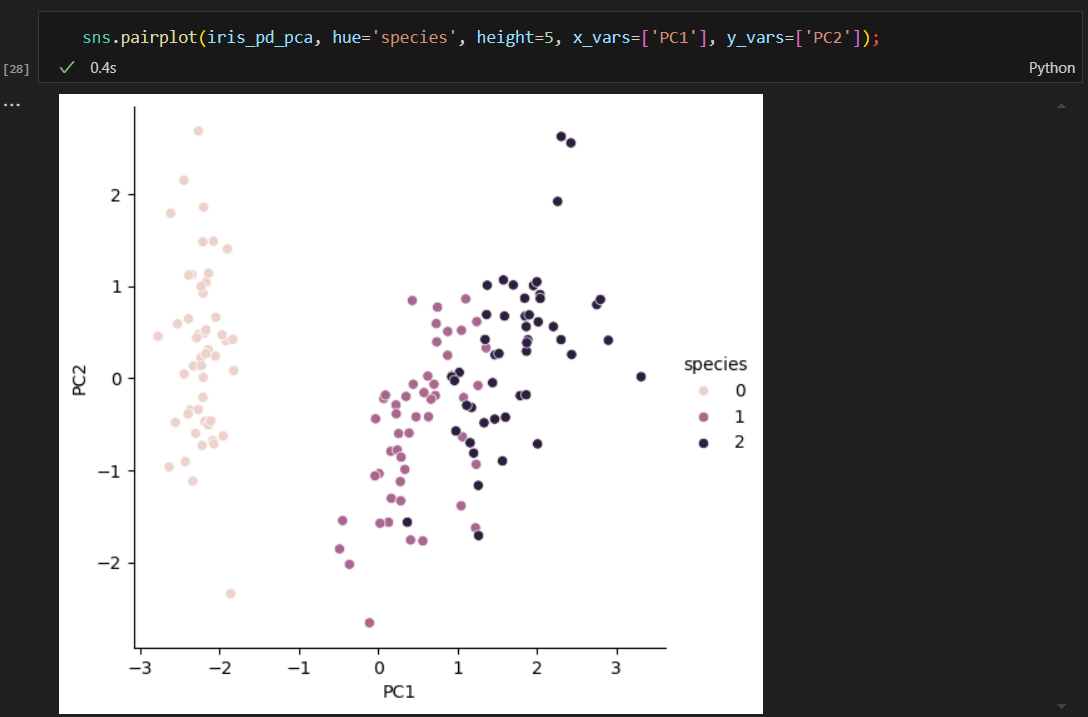
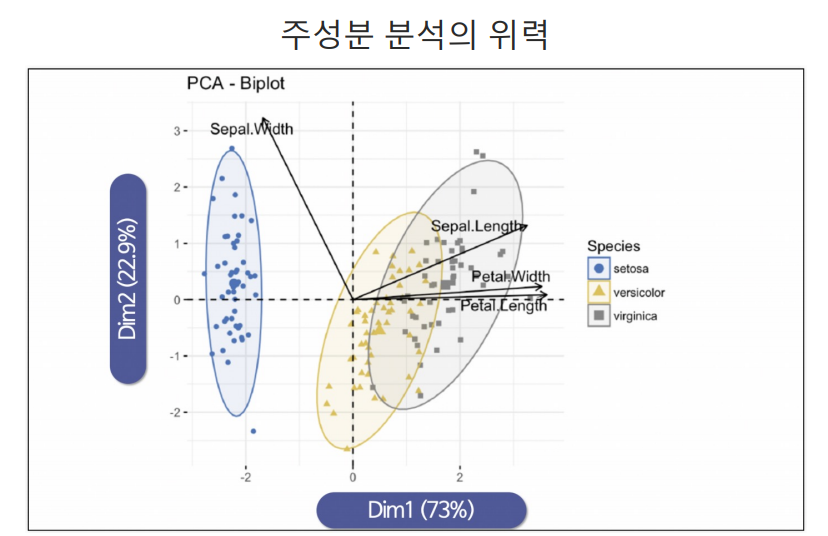
두개의 특성(주성분) 그리기
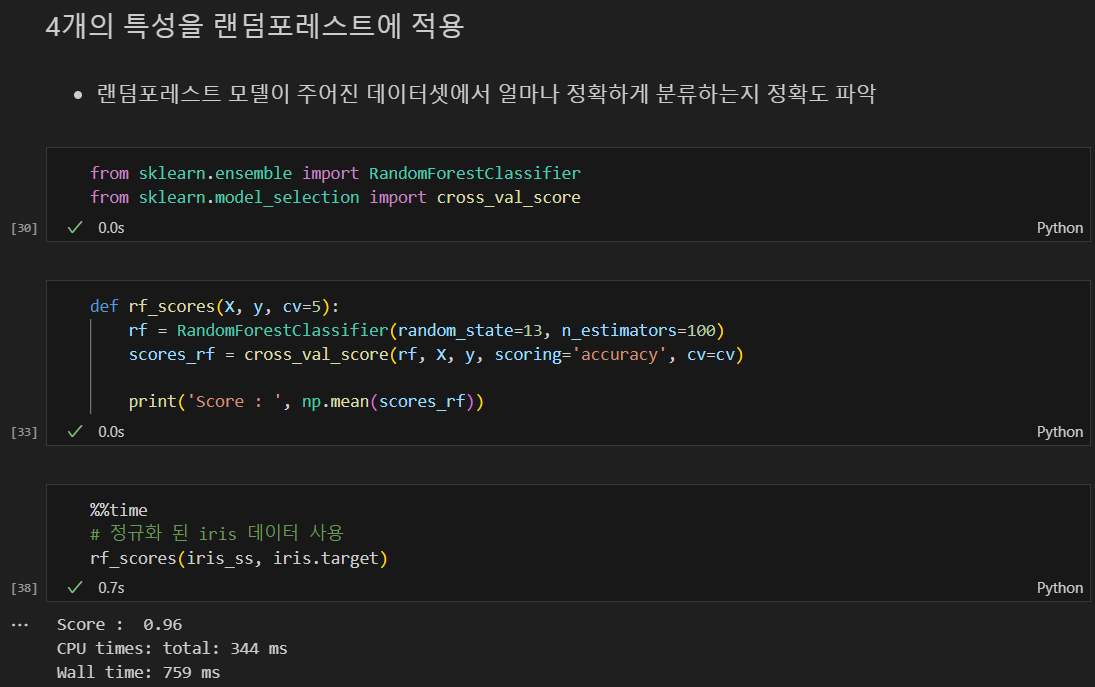
4개의 특성을 랜덤 포레스트에 적용
- 랜덤포레스트 모델이 주어진 데이터셋에서 얼마나 정확하게 분류하는지 정확도 파악
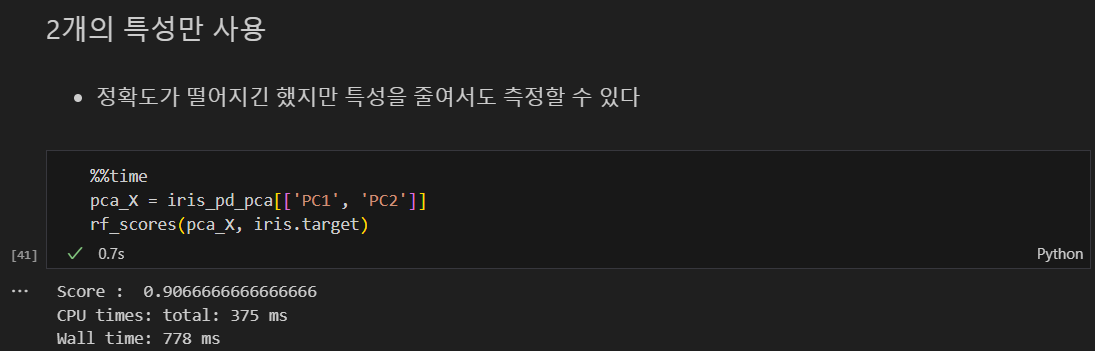
2개의 특성만 사용
wine 데이터로 실습
데이터 불러오기 및 색상 분류
데이터 정규화 및 두개의 주성분으로 줄이기
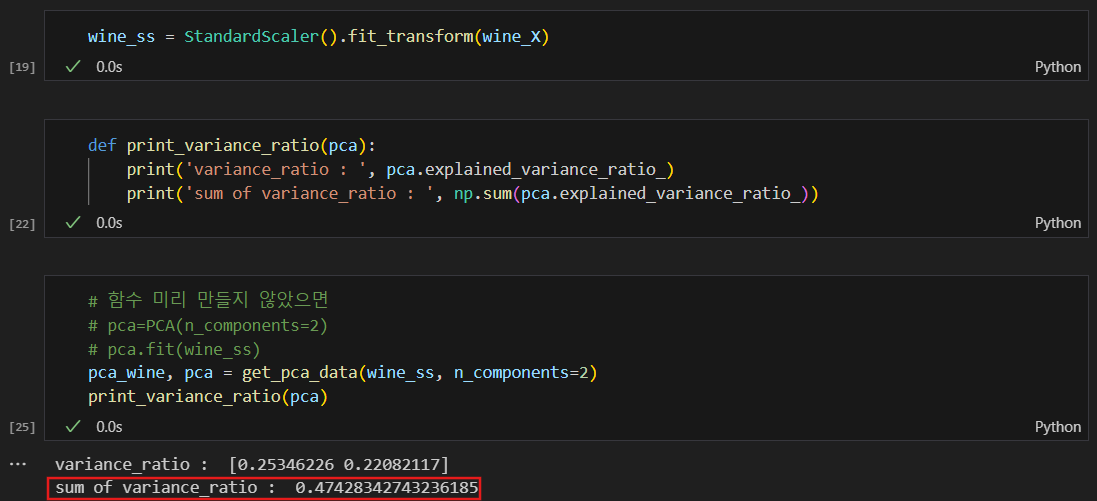
두개의 주성분으로 줄이면, 각 주성분이 데이터 전체 분산에 얼마만큼 차지하는지를 보는 variance_ratio를 보면 두개의 주성분 비율을 합쳐도 전체의 50%가 안되긴 한다.
그래도 그려보기
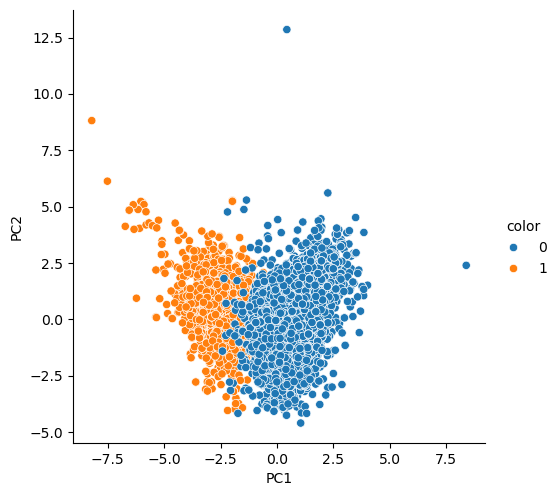
랜덤포레스트에 적용했을 때 원래의 데이터와 큰 차이는 없다.
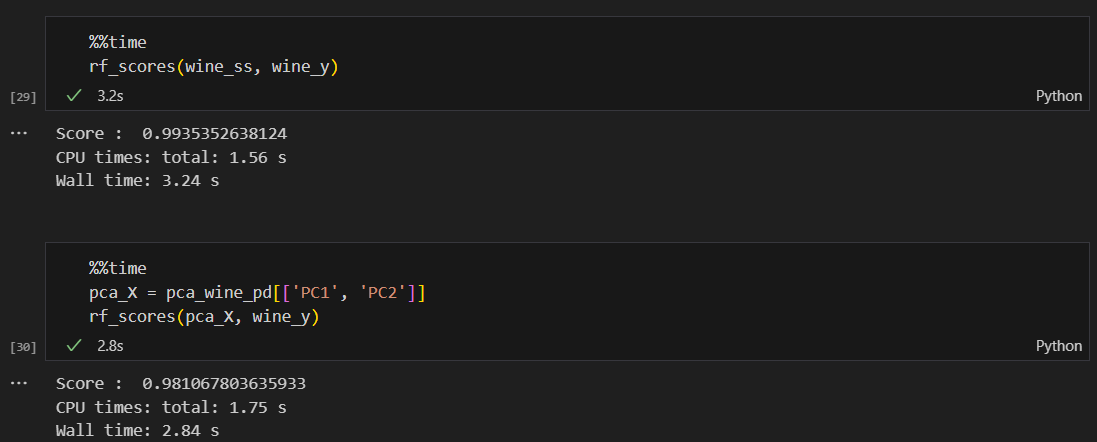
주성분을 3개로 변경
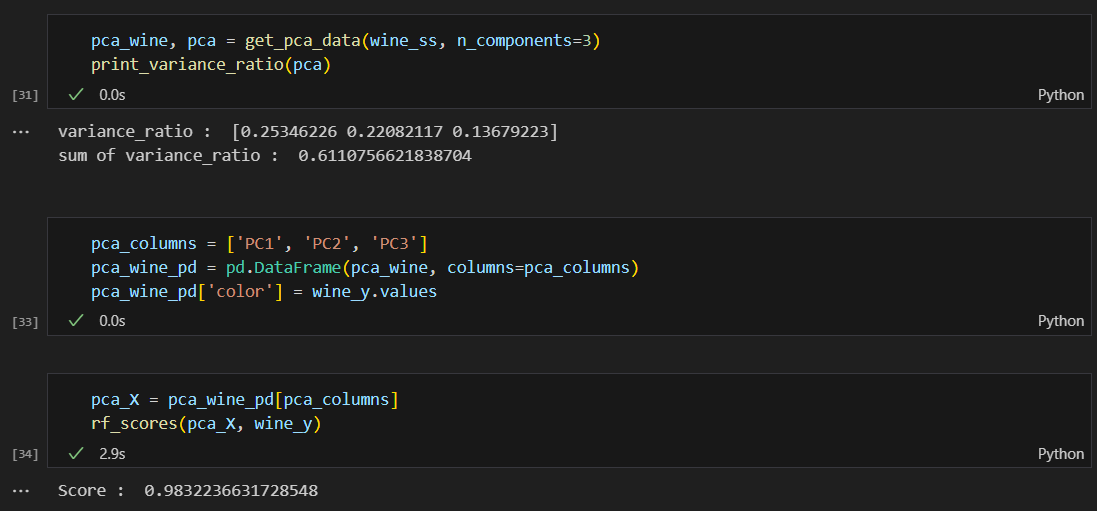
정확도 점수는 0.981 -> 0.983으로 살짝 상승했다.
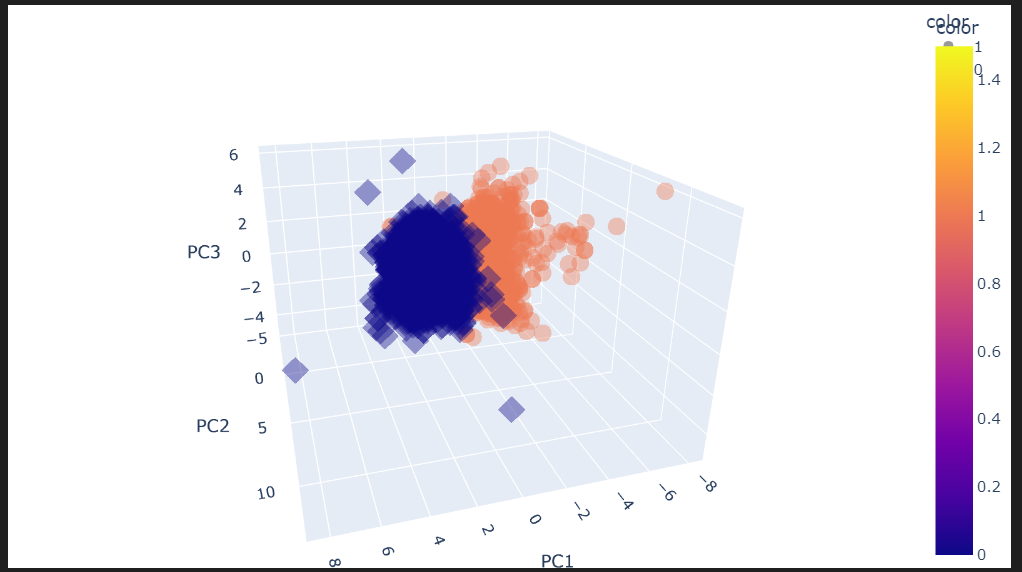
정리하고 3D로 그려보기