서론

문제를 해결한 후, n의 숫자가 소수인지를 판별할 때, 수가 클수록 연산횟수가 비효율적이라는 생각이 들었다.
때문에, 내가 푼 풀이 외에도, 소수를 구하는 알고리즘을 따로 정리하게 되었다.

소수 찾기

문제 설명

1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.

소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.(1은 소수가 아닙니다.)

제한 조건

• n은 2이상 1000000이하의 자연수입니다.

입출력 예

n	result
10	4
5	3

입출력 예 설명

입출력 예 #11부터 10 사이의 소수는 [2,3,5,7] 4개가 존재하므로 4를 반환

입출력 예 #21부터 5 사이의 소수는 [2,3,5] 3개가 존재하므로 3를 반환

문제출처: 프로그래머스

문제 해결 아이디어

1. 각 숫자들이 나눠떨어지는지 제곱근까지만 확인하는 방법.

   • 약수는 대칭을 이루기 때문에 제곱근까지만 탐색을 하면된다.
   • 예를 들어, 8의 약수는 (1x8, 2x4, 4x2, 8x1)로 대칭을 이루게 된다.

2. 에라토스테네스의 체를 사용하는 방법

에라토스네스의 체

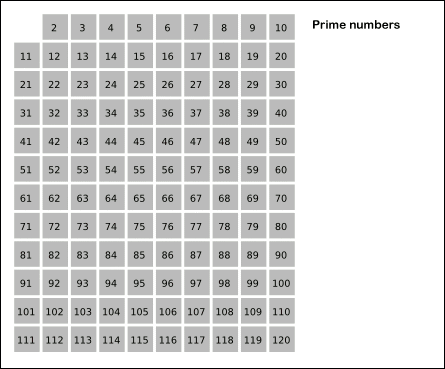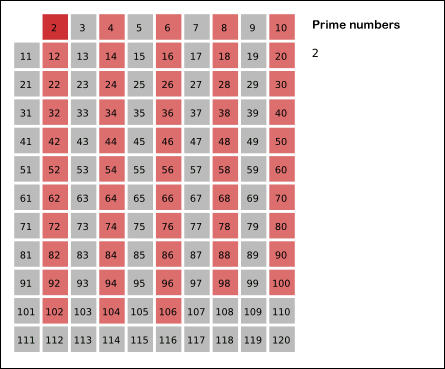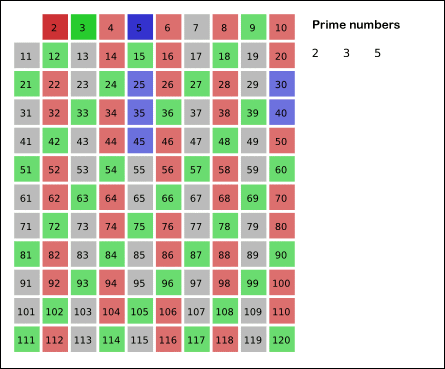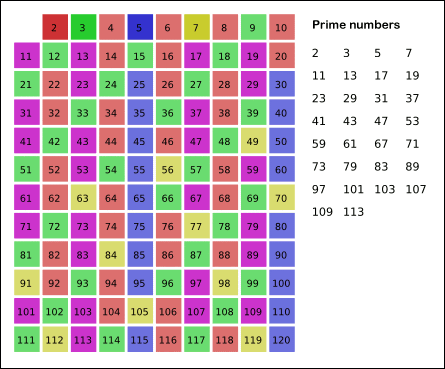
이미지 출처: https://defian.tistory.com/entry/알고리즘-에라토스테네스의-체-C-소수-찾기


탐색하고 있는 숫자의 배수를 제외시킨다.(해당 숫자는 남겨둠)

이렇게 소수가 아닌 수들은 제외가 되며, 나머지는 소수만이 남게 된다.

내 솔루션

#include <string>
#include <vector>
#include <cmath>

using namespace std;

int solution(int n) {
    int answer = 0;
    bool isPrime = true;
    vector<int> v;
    int sq;
    for(int i=2; i<=n; i++) {
        sq = sqrt(i);
        isPrime = true;
        for(int j=2; j<=sq; j++) {
            if(i%j == 0) {
                isPrime = false;
                break;
            }
        }
        if(isPrime)
            v.push_back(i);
    }
    answer = v.size();
    return answer;
}

풀이 설명

제곱근 까지만 탐색하는 문제 해결 아이디어 1번 방법을 사용하여 풀었었다.

n까지의 수를 탐색하면서, 현재 탐색하고 있는 수가 소수인지, 현재 수의제곱근까지 다시 탐색하여 소수인지 판별하였다.

다른 사람 풀이

#include <vector>
#include <cmath>
bool memo[1000000]{ false };

int solution(int n) {
    int answer = 0;
    for (int i = 2; i <= n; i++) {
        if(memo[i])        // 어떤 수의 배수였다면 소수가 아님
            continue;
        answer++;
        // 현재수의 배수부터 N까지 자신의 배수를 소수가 아님으로 메모함
        for (int j=i+i; j <= n; j += i)
            memo[j] = true;
    }
    return answer;
}

풀이 설명

문제 해결 아이디어 2번을 사용하였다.

가장 작은 수부터 탐색.

해당 수의 배수를 전부 제외시키고, 배수로 남지 않은 숫자들이 소수가 된다.

느낀점

소수를 찾는 방법은 여러 방법이 있지만, 하나하나 전부 소수인지를 확인하기 위하여 1부터 탐색하는 방법은 비효율적이고, 연산횟수도 너무 많았다.

그래서 문제를 푼 뒤, 더 연산횟수를 줄일 수 있는 알고리즘이 없을까 찾게 되었고, 에라토스테네스의 체 알고리즘을 공부하게 되었다. 다음부터, 소수를 구하는 알고리즘 문제에서는 좀 더 효율적으로 풀 수 있을 것 같다.