알고리즘
1.[ 알고리즘 ] 빅오 표기법(Big-Oh Notation)

알고리즘의 시간복잡도를 계산하기 위해, 가장 많이 사용되는 방법 중 하나가 바로 빅오 표기법이다.이번에는 빅오표기법을 통해 시간복잡도를 어떻게 계산하는지, 어떤 빅오가 효율적인지 공부했다.T(n)이 다항식으로 표현된 경우, 최고차항의 차수가 빅-오가 된다.$$T(n)=
2.[ 알고리즘 ] 이진탐색

첫번째 인덱스와 마지막 인덱스의 값을 합한 후 절반으로 나눈다.절반으로 나눠 나온 중앙 인덱스의 값과 target 값을 비교한다.만약 target 값보다 작다면 왼쪽을 크다면, 오른쪽을 탐색한다.그럼, 언제까지 이 탐색을 반복해야 할까?탐색하는 first와 last 값
3.[ 알고리즘 ] 이진 탐색 알고리즘의 재귀적 구현

이진탐색 알고리즘의 논리는 재귀적이기 때문에, 충분히 재귀함수로 구현할 수 있다.이진탐색 알고리즘의 논리는 아래와 같은 작업들이 반복된다.중앙 인덱스 값과 target 값을 비교target 값이 더 크다면, start 값을 mid 오른쪽으로, 아니라면 end값을 mid
4.[ 알고리즘 ] 하노이의 탑
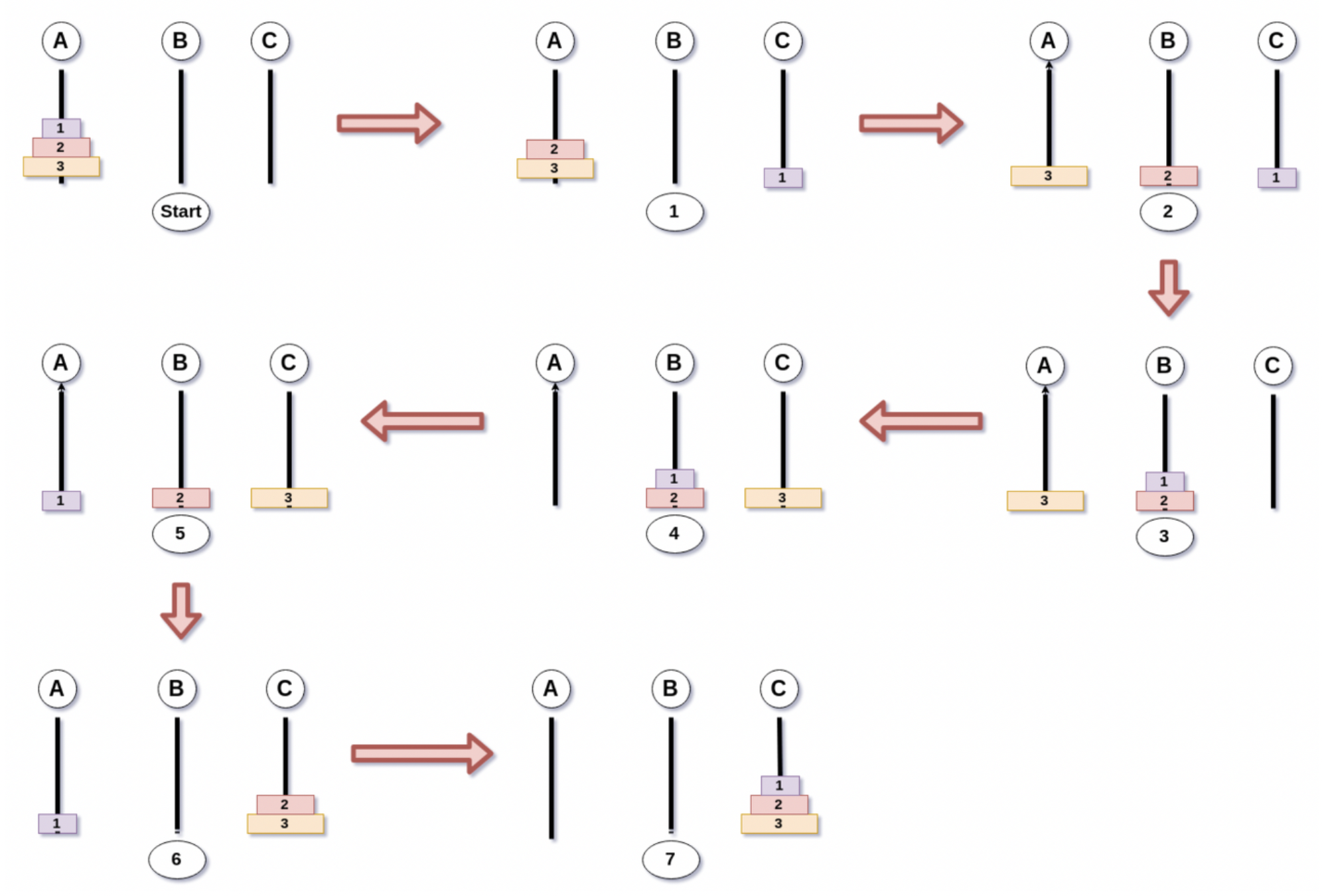
규칙:각 원반은 자신보다 큰 원반 위에만 올 수 있다.한 번에 옮길 수 있는 것은 한개의 원반밖에 없다.어떻게 해결해야 할까?한 번 직접 원반이 있다 생각하고, 그림으로 표현하면 이렇다.작은 원반 n-1개를(맨 아래 원반을 제외한 원반들)을 A에서 B로 이동큰 원반(맨
5.[ 알고리즘 ] 유클리드 호제법

유클리드 호제법이란, 2개의 자연수 또는 정식의 최대공약수를 구하는 알고리즘의 하나이다.호제법이란, 두 수가 서로 상대방 수를 나누어서 결국 원하는 수를 얻는 알고리즘이다.출처: 위키피디아2개의 자연수 a와 b의 나머지를 r이라고 하자.이때, a와 b의 최대공약수 ==
6.[ 알고리즘 ] 프로그래머스: 문자열 내 마음대로 정렬하기

문자열로 구성된 리스트 strings와, 정수 n이 주어졌을 때, 각 문자열의 인덱스 n번째 글자를 기준으로 오름차순 정렬하려 합니다. 예를 들어 strings가 "sun", "bed", "car"이고 n이 1이면 각 단어의 인덱스 1의 문자 "u", "e", "a"로
7.[ 알고리즘 ] 프로그래머스: 두 개 뽑아서 더하기

오늘 푼 문제에 대하여, 내 풀이와 다른 사람 풀이를 비교하고 정리해보려 한다.정수 배열 numbers가 주어집니다. numbers에서 서로 다른 인덱스에 있는 두 개의 수를 뽑아 더해서 만들 수 있는 모든 수를 배열에 오름차순으로 담아 return 하도록 soluti
8.[ 알고리즘 ] 프로그래머스: 소수 찾기

문제를 해결한 후, n의 숫자가 소수인지를 판별할 때, 수가 클수록 연산횟수가 비효율적이라는 생각이 들었다.때문에, 내가 푼 풀이 외에도, 소수를 구하는 알고리즘을 따로 정리하게 되었다.1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution