
📚 이상치 처리
이상치란?
이상치는 일반적인 데이터 값과 편차가 큰 값 (전체 데이터 패턴에서 동떨어진 값) 들을 말한다.
이러한 이상치를 학습 전에 처리하는 과정을 거치지 않으면 데이터에 왜곡이 발생해 원하는 결과를 도출하지 못할 수 있기 때문에 이상치를 처리하는 과정은 필수적이다.
이상치는 두가지로 나눌 수 있는데,
- 지대점 (Leverage point) : 독립변수에 존재하는 이상치
- 아웃라이어 (Outlier) : 종속변수에 존재하는 이상치
데이터 전처리 과정에서 주로 Outlier만을 다루는 경우가 많기에 보통
이상치 = Outlier라고 생각하면 된다.
이상치를 확인하는 방법으론, 단변수의 경우 Boxplot을, 이변수의 경우 Scatter 그래프를 사용한다.
이상치를 확인 후, 검출할 때는 likelihood (통계), Nearest neighbor (데이터 간의 거리), Density (카이제곱 분포), Tukey's Fence (4분위), Z-Score (정규분포) 등이 있는데 여기선 주로 사용하는 Tukey's Fence와 Z-Score에 대해 알아보자.
📚 Tukey's Fence
IQR, InterQuartile Range
Tukey's Fence는 사분위 범위(IQR)를 기반으로 이상치를 처리하는 방법이다. IQR은 세번째 사분위에서 첫번째 사분위를 뺀 값이며 이를 식으로 나타내면
IQR value = Q (Upper Quartile) - Q (Lower Quatile) 이 된다.
코드로 Tukey's Fence를 구현해보자. Tukey's Fence를 구현하기 위해 필요한 library는 다음과 같다.
import numpy as np
import matplotlib.pyplot as plt📚 데이터 셋 준비
data = np.array([3, 30, 35, 40, 45, 48, 49, 50, 51, 52, 53, 55, 60, 65, 90, 95])우선 임의로 데이터 셋을 준비한다.
📚 Boxplot?
우선 Boxplot에 대해 간단하게 알아보자.
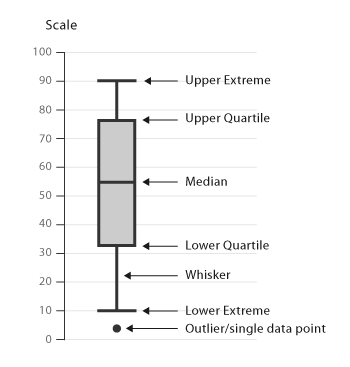
그림을 보면, Boxplot은 크게 최댓값, 3(75%), 2(50%), 1(25%) 사분위, 최솟값으로 나눠지며 최대, 최소보다 크고 작은 값들을 우리는 이상치라고 여긴다.
print(np.median(data)) # 50.5 2사분위
print(np.percentile(data, 25)) # 43.75 1사분위
print(np.percentile(data, 75)) # 56.25 3사분위이와 같은 NumPy 함수를 사용하여 데이터에 대한 각 사분위를 간단하게 구할 수 있다.
📚 IQR value
# IQR Value
iqr_value = np.percentile(data, 75) - np.percentile(data, 25)
# Upper Fence (upper_fence보다 큰 수는 상위 이상치)
upper_fence = np.percentile(data, 75) + (iqr_value * 1.5)
# Lower Fence (lower_fence보다 작은 수는 하위 이상치)
lower_fence = np.percentile(data, 25) - (iqr_value * 1.5)
print(upper_fence, lower_fence) # 75.0 25.0우선 NumPy를 사용하여 구한 3사분위와 1사분위의 값을 빼주어 IQR value를 구한 뒤, 이상치를 구하기 위한 upper_fence와 lower_fence를 구해준다. 이때 구하는 식으론,
Upper Fence, Lower Fence
Upper Fence = Q (3사분위 값) + (IQR value x 1.5)
Lower Fence = Q (1사분위 값) - (IQR value x 1.5)
IQR value에 1.5를 곱해주고 1, 3사분위에 각각 더해고 빼준다.
📚 이상치 제거
result_data = data[(data <= upper_fence) & (data >= lower_fence)] # 이상치 제거
print(result_data) # [30 35 40 45 48 49 50 51 52 53 55 60 65]이제 구한 Upper, Lower Fence를 활용하여 가지고 있는 Raw Data에 Boolean indexing**을 통해 이상치를 걸러준다. Raw Data와 비교해보면 전체 데이터에 비해 매우 크거나 작은 데이터가 삭제된 것을 볼 수 있다.
📚 결과 확인
fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
ax1.set_title('Original Data')
ax1.boxplot(data)
ax2.set_title('Processed Data')
ax2.boxplot(result_data)
plt.show()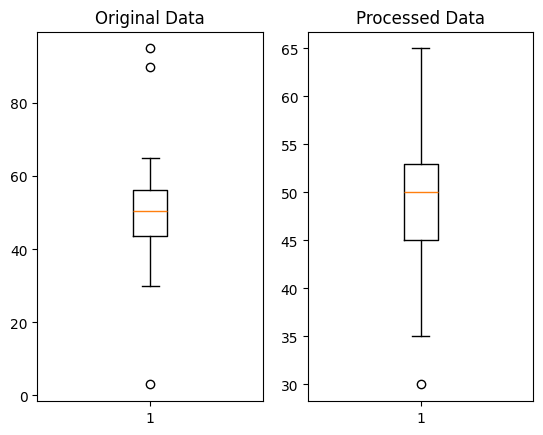
Raw Data와 이상치가 처리된 데이터로 Boxplot을 그려보면, 전체 데이터 값과 편차가 큰 값들이 많이 제거된 것을 볼 수 있다.
📚 Z-Score
Z-Score (표준 점수)
표준 점수란 데이터의 평균과 표준편차의 차이를 말한다. 이때 표준 점수는
표준 점수 = (데이터 포인트 - 데이터의 평균) / 데이터의 표준편차
위와 같이 구할 수 있으며, threshold를 지정해 제거하고자 하는 이상치의 범위를 설정할 수 있다.
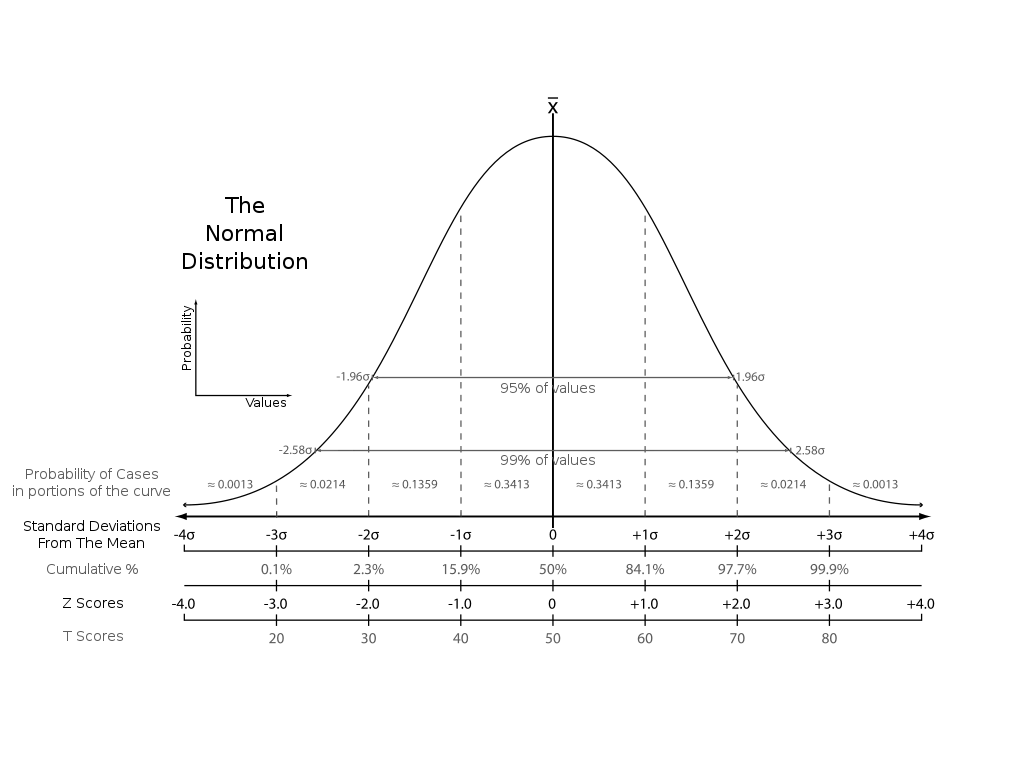
위 그림의 Z Scores를 통해 주어진 데이터 포인트가 평균과 얼마나 떨어져 있는지를 판단할 수 있으며, 임의로 지정한 threshold 값을 통해 얼마나 엄격하게 이상치를 판별할 지 정할 수 있다.
이제 Z-Score를 코드로 구현해보자. Z-Score를 구현하기 위해 필요한 library는 다음과 같다.
import numpy as np
from scipy import stats📚 데이터 셋 준비
data = np.array([3, 30, 35, 40, 45, 48, 49, 50, 51, 52, 53, 55, 60, 65, 90, 95])Tukey's Fence에서 사용했던 데이터 셋을 그대로 사용한다.
📚 Z-Score 도출
print(stats.zscore(data))
# [-2.32218008 -1.02440286 -0.78407374 -0.54374462 -0.30341551 -0.15921804
# -0.11115222 -0.06308639 -0.01502057 0.03304525 0.08111108 0.17724272
# 0.41757184 0.65790095 1.85954653 2.09987565]이와 같이 scipy 라이브러리의 stats.zscore() 함수를 사용하면 쉽게 Z-Score를 구할 수 있다.
📚 threshold 설정 및 결과 확인
zscore_threshold = 2.0
print(~(np.abs(stats.zscore(data)) > zscore_threshold)) # Boolean Mask
# [False True True True True True True True True True True True
# True True True False]
print(data[~(np.abs(stats.zscore(data)) > zscore_threshold)]) # Boolean Indexing
# [30 35 40 45 48 49 50 51 52 53 55 60 65 90]임의로 설정한 zscore_theshold를 사용하여 Boolean Mask를 만들고, 이를 사용하여 Boolean indexing을 하면 이상치가 제거 된 것을 학인할 수 있다. 이때 NumPy의 abs() 함수를 사용해 모든 Z-Score에 절댓값을 씌워준 뒤 (차이만 구하면 되기에), zscore_threshold와 비교해준다.
