베이즈 통계학 맛보기

c0natus·2022년 1월 29일
ai math
0

AI Math

목록 보기
7/9
  • 베이즈 정리는 새로운 정보가 추가될 때, 정보를 업데이트하는 이론적 기반을 소개하는 내용이다.

1. 조건부 확률

  • 조건부 확률 P(A∣B)P(A|B)는 사건 BB가 일어난 상황에서 사건 AA가 발생할 확률이다.

  • 수학적으로는 아래와 같이 나타낸다.


P(A∣B)=P(A∩B)P(B)P(A|B) = \frac{P(A \cap B)}{P(B)}

  • 조건부 확률은 product rule이라고도 얘기한다.

  • 베이즈 정리는 조건부확률을 이용해 정보를 갱신하는 방법을 알려준다.

  • AA와 BB가 서로 독립이라면 P(A∣B)=P(A)P(A|B) = P(A)이고 P(A∩B)=P(A)⋅P(B)P(A\cap B) = P(A) \cdot P(B)이다.

2. 확률 법칙

Product rule(conditional probability)


P(A∩B)=P(A∣B)P(B)=P(B∣A)P(A)P(A\cap B) = P(A|B)P(B) = P(B|A)P(A)

Sum rule(marginalization)


P(A)=P(P(A∩B)∪P(A∩¬B))=P(A∩B)+P(A∩¬B)P(A) = P(P(A \cap B)\cup P(A \cap \neg B)) = P(A \cap B) + P(A \cap \neg B)

  • 일반적으로 아래와 같이 표현한다.
P(X1=x1,⋯ ,Xd−1=xd−1)=∑xd∈XdP(X1=x1,⋯ ,Xd−1=xd−1,Xd=xd)P(X_1 = x_1, \cdots , X_{d-1} = x_{d-1}) = \sum\limits_{x_d \in X_d} P(X_1 = x_1, \cdots , X_{d-1} = x_{d-1}, X_d = x_d)

  • 위의 과정을 $X_d$에 대해서 marginalize out 한다라고도 부른다.

  • P(X1=x1,⋯ ,Xd−1=xd−1)P(X_1 = x_1, \cdots , X_{d-1} = x_{d-1}) 분포를 marginal 분포라고 부른다.

  • 또한, Projection을 통해 차원을 하나 줄이는 것으로 해석할 수도 있다.

Chain rule


P(X1,⋯ ,Xn)=P(Xn∣X1,⋯ ,Xn−1)⋅P(X1,⋯ ,Xn−1)P(X_1, \cdots , X_n) = P(X_n|X_1, \cdots , X_{n-1}) \cdot P(X_1, \cdots, X_{n-1})

P(X1,⋯ ,Xn−1)=P(Xn−1∣X1,⋯ ,Xn−2)⋅P(X1,⋯ ,Xn−2)P(X_1, \cdots, X_{n-1}) = P(X_{n-1}|X_1, \cdots, X_{n-2}) \cdot P(X_1, \cdots, X_{n-2})

P(X1,⋯ ,Xn)=P(Xn−1∣X1,⋯ ,Xn−2)⋅P(X1,⋯ ,Xn−2)⋅... ⋅P(X2∣X1)⋅P(X1)P(X_1, \cdots , X_n) = P(X_{n-1}|X_1, \cdots, X_{n-2}) \cdot P(X_1, \cdots, X_{n-2}) \cdot ... \ \cdot P(X_2|X_1)\cdot P(X_1)

∴P(X1,⋯ ,Xn)=∏i=1nP(Xi∣X1,⋯ ,Xi−1)\therefore P(X_1, \cdots , X_n) = \prod_{i=1}^nP(X_i|X_1, \cdots,X_{i-1})

3. 베이즈 정리

  • P(A∣B)P(A|B)와 P(B)P(B)를 알고있는 상태에서 P(A)P(A)가 주어졌을 때, P(B∣A)P(B|A)는 다음과 같이 계산한다.

P(B∣A)=P(B)P(A∣B)P(A)P(B|A) = P(B)\frac{P(A|B)}{P(A)}

  • P(B∣A)P(B|A)를 사후 확률(posterior), P(B)P(B)를 사전확률(prior), P(A∣B)P(A|B)를 가능도(likelihood), P(A)P(A)를 증거(evidence)라고 볼 수 있다.

  • 즉, BB가 예측된 확률분포의 모수 θ\theta이고, AA 실제 데이터 D\mathcal{D}로 볼 수 있다.

3.1. 조건부 독립

  • CC가 주어졌을 때 P(A∩B∣C)=P(A∣C)⋅P(B∣C)P(A\cap B|C) = P(A|C)\cdot P(B|C)가 성립되면, AA와 BB는 독립이다.

Theroem

  • CC가 주어졌을 때, AA와 BB는 독립이면 아래와 같은 식이 성립한다.
  1. P(A∩B∣C)=P(A∣C)⋅P(B∣C)→definitionP(A\cap B|C) = P(A|C)\cdot P(B|C) \rightarrow \text{definition}
  2. P(A∣B∩C)=P(A∣C)P(A|B \cap C) = P(A|C)
  3. P(B∣A∩C)=P(B∣C)P(B|A \cap C) = P(B|C)

P(A∩B∩C)=P(A∩B∣C)P(C)=P(A∣C)P(B∣C)P(C)→definitionP(A\cap B \cap C) = P(A \cap B|C)P(C) = P(A|C)P(B|C)P(C) \rightarrow \text{definition}

P(A∩B∩C)=P(A∣B∩C)P(B∣C)P(C)→chain ruleP(A\cap B \cap C) = P(A|B \cap C)P(B|C)P(C) \rightarrow \text{chain rule}

∴P(A∣B∩C)=P(A∣C)\therefore P(A|B \cap C) = P(A|C)

3.2. 예제 - 1: 사후확률

COVID-99의 발병률이 10%로 알려져있다. COVID-99에 실제로 걸렸을 때 검진될 확률은 99%, 실제로 걸리지 않았는데 검진될 확률이 1%라고 하자.

Q)Q) 질병에 걸렸다고 검진 결과가 나왔을 때, 정말로 COVID-99에 감염되었을 확률은?

  • θ\theta를 발병률(관찰 불가)라 하고, D\mathcal{D}를 검진될 확률이라고 하자.

  • 사전확률: P(θ)=0.1P(\theta) = 0.1

  • 가능도: P(D∣θ)=0.99,P(D∣¬θ)=0.01P(\mathcal{D}|\theta) = 0.99, P(\mathcal{D}|\neg\theta) = 0.01

  • 증거: P(D)=∑θP(D∣θ)P(θ)=0.99×0.1+0.01×0.9=0.108P(\mathcal{D}) = \sum\limits_{\theta}P(\mathcal{D}|\theta)P(\theta) =0.99 \times 0.1 + 0.01 \times 0.9=0.108

  • 사후확률: P(θ∣D)=0.1×0.990.108≈0.916P(\theta|\mathcal{D}) = 0.1\times\frac{0.99}{0.108} \approx 0.916

오검진될 확률(1종 오류)가 10%일 때, 사후확률을 구해보자.

  • 가능도: P(D∣θ)=0.99,P(D∣¬θ)=0.1P(\mathcal{D}|\theta) = 0.99, P(\mathcal{D}|\neg\theta) = 0.1

  • 증거: P(D)=0.99×0.1+0.1×0.9=0.189P(\mathcal{D}) = 0.99 \times 0.1 + 0.1 \times 0.9=0.189

  • 사후확률: P(θ∣D)=0.1×0.990.189≈0.524P(\theta|\mathcal{D}) = 0.1\times\frac{0.99}{0.189} \approx 0.524

  • 오탐률(False alarm)이 오르면 테스트의 정밀도(Precision)가 떨어진다.

  • 사전확률이 없으면 베이즈 통계학을 하기 어렵다.

  • 사전확률이 없는 경우 임의로 설정한다. → 신뢰도는 떨어진다.

3.3. confusion matrix

  • 정밀도는 오탐지율과 민감도에 영향을 받는다.

precision(posterior)=recall×prior(P(θ))recall×prior(P(θ))+false alarm×prior(P(¬θ))\text{precision(posterior)} = \frac {\text{recall} \times \text{prior}(P(\theta))} {\text{recall} \times \text{prior}(P(\theta)) + \text{false alarm} \times \text{prior}(P(\neg \theta))}

  • 위의 예제를 confusion matrix로 나타내면 아래와 같다.

↓\boldsymbol{\downarrow}

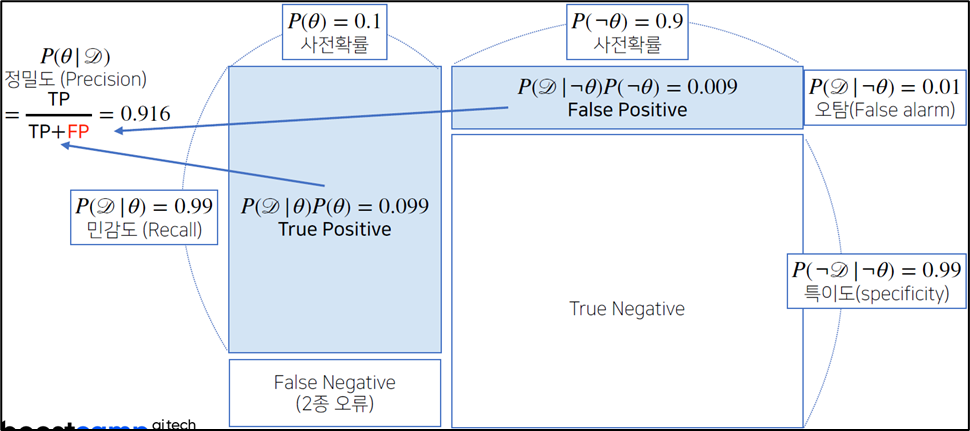
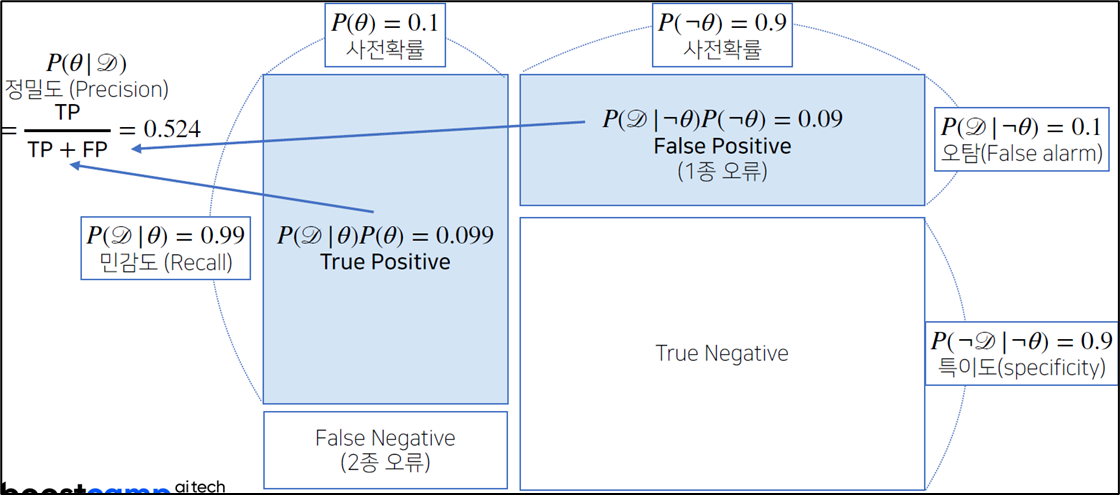
3.4. 갱신된 사후확률

  • 베이즈 정리를 통해 새로운 데이터가 들어왔을 때, 앞서 계산한 사후확률을 사전확률로 사용해 갱신된 사후확률을 계산할 수 있다. → 베이즈 통계학의 장점

P(θ∣D)=P(θ)P(D∣θ)P(D)P(\theta|\mathcal{D}) = P(\theta)\frac{P(\mathcal{D}|\theta)}{P(\mathcal{D})}

  • 위의 결과값 P(θ∣D)P(\theta|\mathcal{D})를 P(θ∗)P(\theta^*)라고 하자.

  • 새로운 데이터가 들어왔을 때, 갱신된 사후확률은 아래와 같이 계산할 수 있다.


P(θ∗∣D∗)=P(θ∗)P(D∣θ)P(D∗)=P(θ∣D)P(D∣θ)P(D∗)P(\theta^*|\mathcal{D}^*) = P(\theta^*)\frac{P(\mathcal{D}|\theta)}{P(\mathcal{D}^*)} = P(\theta|\mathcal{D})\frac{P(\mathcal{D}|\theta)}{P(\mathcal{D}^*)}

  • 데이터가 추가되면 가능도는 그대로 유지한 채, evidence와 prior만 갱신된다.

3.5. 예제 - 2: 갱신된 사후확률

QQ) 예제 - 1에서 COVID-99 판정을 받은 사람이 두 번째 검진을 받았을 때도 양성이 나왔을 때, 진짜 COVID-99에 걸렸을 확률은?

  • 앞서 계산한 P(θ∣D)=0.1×0.990.189≈0.524P(\theta|\mathcal{D}) = 0.1\times\frac{0.99}{0.189} \approx 0.524 이다.

  • 갱신된 P(θ∗)=P(θ∣D)≈0.524P(\theta^*) = P(\theta|\mathcal{D}) \approx 0.524 이다.

  • 갱신된 P(D∗)=0.99×0.524+0.1×0.476≈0.566P(\mathcal{D}*) = 0.99 \times 0.524 + 0.1 \times 0.476 \approx 0.566 이다.

  • 갱신된 사후확률 P(θ∗∣D∗)=P(θ∗)P(D∣θ)P(D∗)=0.524×0.990.566≈0.917P(\theta^*|\mathcal{D}^*) = P(\theta^*)\frac{P(\mathcal{D}|\theta)}{P(\mathcal{D}^*)} = 0.524 \times \frac{0.99}{0.566} \approx 0.917 이다.

  • 세번째 검사에도 양성이 나오면 정밀도는 99.1% 까지 갱신된다.

3.6. 인과관계 추론

  • 조건부 확률은 유용한 통계적 해석을 제공하지만, 인과관계(causality)를 추론할 때 사용하면 안된다.

  • 인과관계는 데이터 분포의 변화에 강건한(robust) 예측모형을 만들 때 필요하다.

  • 인과관계를 알아내기 위해서는 중첩요인(confounding factor)의 효과를 제거하고, 원인에 해당하는 변수로만 인과관계를 추론해야 한다.

  • 만약 중첩효요인의 효과를 제거하지 않으면, 가짜 연관성(spurious correlation)이 나온다.

예제

  • 위의 예제에서 중첩요인(ZZ: 신장결석 크기)의 효과를 제거하지 않으면, 전체적으로(overall) 치료법 b가 더 나은 것으로 보인다.

  • 이는 심슨의 역설(Simpson's paradox)로, 부분에서 성립하는 대소 관계는 전체를 보았을 때 역전될 수 있다.

  • P(R∣T)=P(R∣T,Z)P(Z∣T)+P(R∣T,Zc)P(Zc∣T)P(R|T) = P(R|T,Z)P(Z|T) + P(R|T,Z^c)P(Z^c|T) → paradox가 생기는 이유

  • P(Z∣T)P(Z|T)과 P(Zc∣T)P(Z^c|T)는 weight로 두 사람이 큰 시장 결석과 작은 신장 결석을 수술한 비율이 달라서 paradox가 생긴다.

  • 이를 해결하기 위해 do(T=a)do(T = a)라는 조정(intervention) 효과를 통해 ZZ의 개입을 제거해야 한다.

  • 이것은 신장 결석에 상관없이 모든 환자가 치료법 a를 선택했다고 가정하는 것이다.

  • 즉, P(Z∣T)P(Z|T)과 P(Zc∣T)P(Z^c|T)대신 P(Z)와P(Zc)P(Z)와 P(Z^c)를 weight로 사용한다.

  • 이것에 대해 추상적으로는 이해가 되는데, 명확한 이해는 아직 잘 안 된다...

  • 극단적으로 a의 z=0, z=1 성공 확률이 100%라고 생각하면 조금은 이해가 된다...(?)

치료법 a


Pa(R=1)=∑z∈{0,1}Pa(R=1∣T=a,Z=z)P(Z=z)P^{a}(R=1) = \sum\limits_{z\in\{0,1\}}P^{a}(R=1|T=a,Z=z)P(Z=z)

∴Pa(R=1)=8187×(87+270)700+192263×(263+80)700≈0.8325\therefore P^{a}(R=1) = \frac{81}{87} \times \frac{(87+270)}{700} + \frac{192}{263} \times \frac{(263+80)}{700} \approx 0.8325

치료법 b


Pb(R=1)=∑z∈{0,1}Pb(R=1∣T=a,Z=z)P(Z=z)P^{b}(R=1) = \sum\limits_{z\in\{0,1\}}P^{b}(R=1|T=a,Z=z)P(Z=z)

∴Pb(R=1)=234270×(87+270)700+5580×(263+80)700≈0.7789\therefore P^{b}(R=1) = \frac{234}{270} \times \frac{(87+270)}{700} + \frac{55}{80} \times \frac{(263+80)}{700} \approx 0.7789

  • 중첩요인의 효과를 제거하면, 치료법 a가 더 낫다는 것을 알 수 있다.

  • 이처럼 중첩요인의 효과를 제거하면, 데이터 분석 시에 좀 더 안정적인 정책 분석이나 예측모형의 설계가 가능하다.

  • 따라서 단순히 조건부확률만으로 데이터 분석을 하는 것은 위험하고, 데이터에서 추론할 수 있는 사실이나 데이터가 생성되는 원리, 도메인 지식 등을 활용해야만 인과관계 추론이 가능하다.

  • 인과관계 추론이 가능해지면, 강건한 데이터모형을 만들 수 있다.

References

profile
c0natus
Done is Better Than Perfect
이전 포스트

통계학 맛보기 - 보충

다음 포스트

CNN 첫 걸음

0개의 댓글