1. 신경망(neural network)
- 이전 포스트에서는 선형모델을 살펴보았지만, 이번엔
비선형모델인 신경망에 대해 알아보자.
-
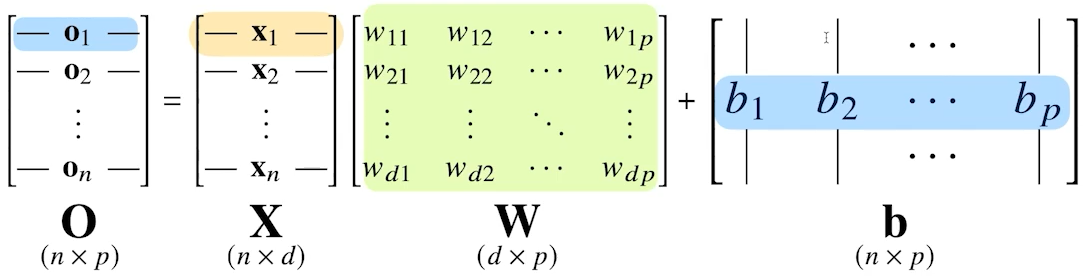
각 행벡터 oi는 데이터 xi와 가중치 행렬 W 사이의 행렬곱과 절편 b 벡터(<b1,⋯,bp>)의 합으로 표현된다고 가정하자.
-
노름(norm)과 행렬에서 살펴보았듯이, 행렬은 데이터와 연산자 기능 수행한다. X는 데이터, W는 연산자 기능을 수행한다고 볼 수 있다.
-
W의 차원에 따라 결과 값인 O의 차원이 결정된다. 위의 그림에서는 데이터가 d차원에서 p차원으로 바뀌게 된다.
-
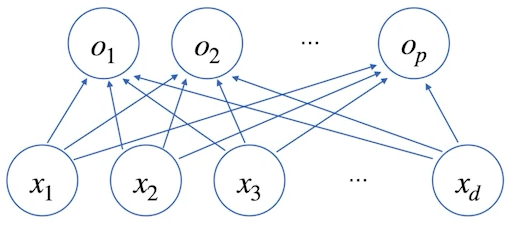
이를 도식화하면, 아래와 같다.
-
행벡터 xk의 원소가 <xk1,⋯,xkd>라하고 행벡터 ok의 원소가 <ok1,⋯,okp>라 하자.
-
이때, xki가 okj에 영향을 끼치는 정도는 wij이다.
-
위의 그림은 데이터 1개에 대해 도식화한 것이다.
1.1. softmax
-
신경망을 선형회귀처럼 regression에 사용할 수 있지만, classification에서도 사용할 수 있다.
-
신경망을 classification에 사용하는 방법 중 하나는 softmax 함수를 사용하는 것이다.
-
softmax이외에도 sigmoid 등의 방법이 있다.
-
softmax는 k개 분류, sigmoid는 이진 분류에 사용된다.
softmax(o)=(k=1∑pe(ok)e(o1),⋯,k=1∑pe(ok)e(op))
-
출력 벡터 o에 softmax 함수를 합성하면, 확률벡터가 되므로 특정 틀래스 k에 속할 확률로 해석할 수 있다.
-
따라서 분류 문제를 풀 때, 선형모델과 softmax 함수를 함께 사용하여 예측한다.
-
추론을 할 경우 최대값을 가진 주소만 1로 나타내는 연산인 원-핫(one-hot) 벡터를 사용해서 softmax를 사용하지 않는다.
-
따라서 학습이 아니라 추론을 할 경우, 굳이 softmax 함수를 사용하지 않아도 된다.
import numpy as np
def softmax(vec):
numerator = np.exp(vec - np.max(vec, axis = -1, keepdims = True))
denominator = np.sum(numerator, axis = -1, keepdims = True)
return numerator / denominator
print(softmax([1, 2, 0]))
1.2. 활성함수(activation function)
- 신경망은
선형모델과 softmax 같은 활성함수를 합성한 함수이다.
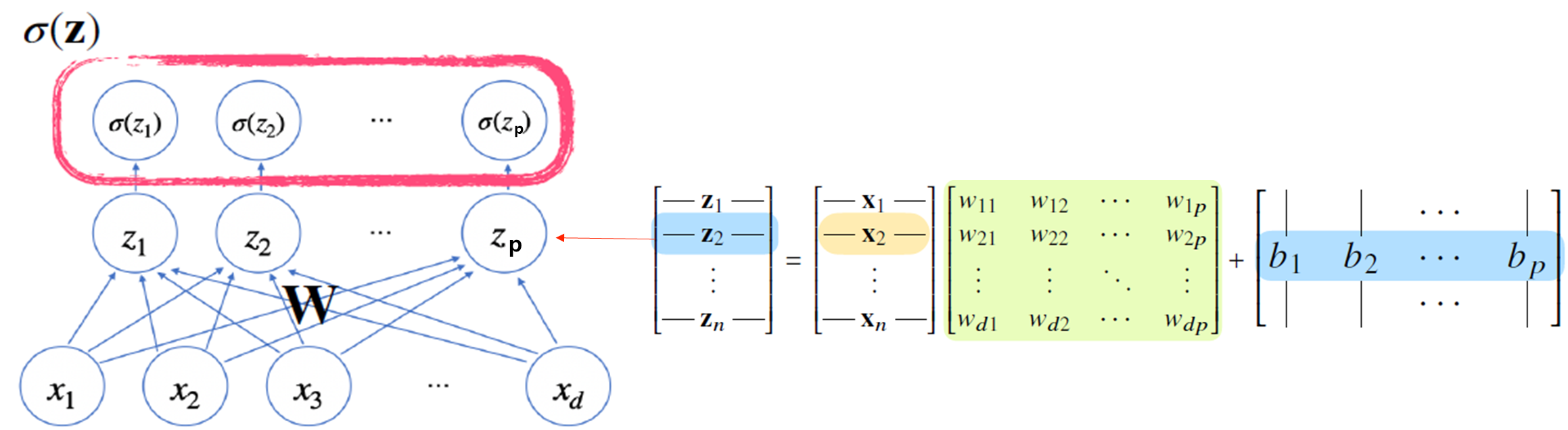
zk=<z1,⋯,zp>
σ(zk)=<σ(z1),⋯,σ(zp)>
σ(zk)=σ(xkW+b)
hk=σ(zk)=<σ(z1),⋯,σ(zn)>
-
활성함수 σ는 비선형함수로 잠재벡터 z=(z1,⋯,zp)의 각 노드에 개별적으로 적용하여 새로운 잠재백터 h를 만든다.
-
잠재벡터는 hidden vector 혹은 neuron이라고 부른다.
-
이처럼 활성함수를 한번 사용한 기본적인 신경망을 퍼셉트론(perceptron)이라고 한다.
-
활성함수는 R 위에 정의된 비선형(nonlinear)함수이다.
-
활성함수를 쓰지 않으면, 층이 깊게 쌓여도 층이 한 개인 것과 다르지 않기 때문에 딥러닝은 선형모형과 차이가 없어진다.
-
시그모이드(sigmoid)나 하이퍼볼릭 탄젠트(tanh) 함수를 전통적으로 많이 사용했지만, gradient vanishing문제로 딥러닝에선 ReLU 함수를 많이 사용한다.
1.3. 2층 신경망
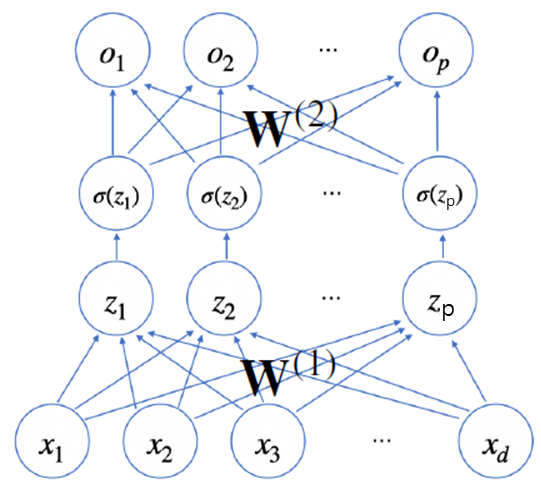
-
위의 신경망은 잠재벡터(hidden vector) h에서 가중치 행렬 W(2)와 b(2)를 통해 다시 한 번 선형변환 해서 출력하는, 2층(2-layers) 신경망이다.
-
W(2)와 W(1)를 파라미터로 가진다.
σ(zk)=σ(xkW(1)+b(1))
hk=<σ(z1),⋯,σ(zn)>
ok=hkW(2)+b(2)
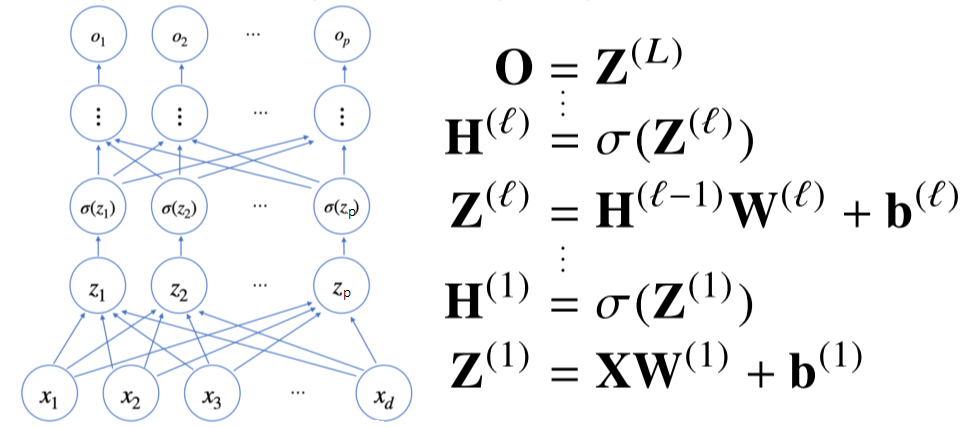
2. 순전파(forward propagation)
-
이처럼 반복적으로 층을 쌓는 것을 다층 퍼셉트론(MLP: multi-layer perceptron)이라고 한다.
-
σ(Z)는 (σ(z1),⋯,σ(zn))으로 이루어진 행렬이다.
-
MLP의 파라미터는 L개의 가중치 행렬 W(L),⋯,W(1)와 L개의 절편 b1,⋯,bL로 이루어져 있다.
-
l=1,⋯,L까지 순차적인 신경망 계산하는 과정을 순전파라 부른다.
-
이론적으로 2층 신경망으로도 임의의 연속함수에 근사할 수 있다. 이를 universal approximation theorem이라고 한다.
-
하지만, 층이 깊을수록 근사하는데 필요한 뉴런(노드)의 숫자가 훨씬 빨리 줄어들어 계산 관점에서 좀 더 효율적으로 학습이 가능하다.
-
그렇지만, 층이 깊을수록 최적화하기에 어렵기 때문에 학습이 어려울 수 있다. → 나중에 CNN residual block에서 다시보자.
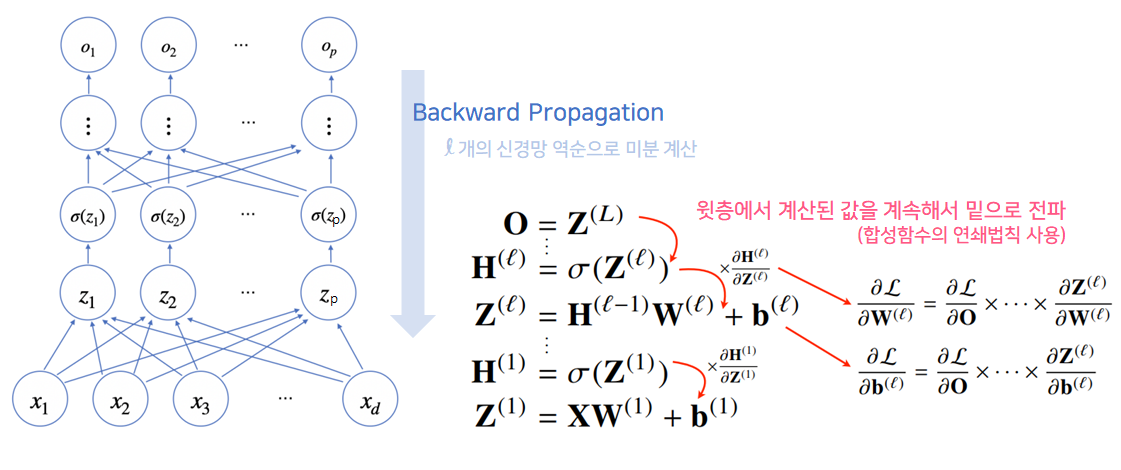
3. 역전파(backward propagation)
- 딥러닝은
역전파 알고리즘을 이용해 각 층에 사용된 파라미터 {W(l),b(l)}l=1L를 학습한다.
-
O는 데이터 x1,⋯,xn(←xk=<x11,⋯,x1d>)를 모두 순전파한 결과를 보여주는 행렬이다.
-
마지막에 활성함수를 곱해주지 않은 것은 추론을 하는 과정으로 원-핫 벡터를 사용하기 때문인 것으로 보인다.
-
손실 함수를 L이라 했을 때, L은 1×p 행렬이 된다. →L=[l1,⋯,lp]
-
경사하강법과 MSE를 통해 최적화할 경우, 손실 함수 L의 k 행(lk)의 값은 n1j=1∑d(ojk−yjk)2이 된다.
-
SGD과 MSE를 통해 최적화할 경우, 손실 함수 L의 k 행(lk)의 값은 batch size1j=1∑d(ojk−yjk)2이 된다.
- j번째 데이터의 실제 값([yj1,⋯,yjp])중 k번째 값(yjk)에, 신경망이 j번째 데이터에 대해 예측한 값([oj1,⋯,ojp])의 k번째 값(ojk)을 빼주어 제곱한다.
- 이를 각 k번쩨 값에 대해
d개의 데이터에 대해 손실 값을 모두 더해주고 평균을 내준 것들이 손실 함수 L를 이룬다.
-
손실 함수 L과 경사하강법으로 각 가중치 W(l)를 학습시킬 때, 선형 회귀의 β를 계산할 때처럼, 각 가중치에 대한 그레디언트 벡터를 계산해야한다.
-
각 가중치에 대한 그레디언트 벡터를 구하는 식은 ∂W(l)∂L이다.
-
바로 ∂W(l)∂L의 값을 바로 구할 수 없기 때문에, chain rule을 활용해 ∂W(L)∂L부터 ∂W(1)∂L까지 역순으로 순차적으로 구해야 한다.
- ∂W(L)∂L = ∂O(L)∂L∂W(L)∂O(L)
- ∂W(L−1)∂L = ∂O(L)∂L∂H(L−1)∂O(L)∂Z(L−1)∂H(L−1)∂W(L−1)∂Z(L−1)
- ∂W(L−2)∂L = ∂O(L)∂L∂H(L−1)∂O(L)∂Z(L−1)∂H(L−1)∂H(L−1)∂Z(L−1)∂Z(L−2)∂H(L−1)∂W(L−2)∂Z(L−2)
-
위의 구조에서 파란색 부분을 보면 앞서 계산된 결과를 재활용해서 계산하는 구조라는 것을 알 수 있다.
-
연산에 사용된 부분이 재사용가능 하다는 것을 토대로 역순으로 gradient가 propagation된다하여 Backpropagation이라고 한다.
-
b에 대해서도 동일하게 적용가능하다.
-
딥러닝에서 역전파 알고리즘은 합성함수 미분법인 연쇄법칙(chain-rule) 기반 자동미분(auto-differentiation)을 사용한다.
-
자동미분을 사용하는 이유는 아래의 두 번째 reference를 참고하자. → 간단하게 말하면 복잡한 식의 미분을 쉽게하기 위한 방법이다.
z=(x+y)2을 x에 대해 미분하는 것을 연쇄법칙기반 자동미분으로 해결해보자.
w=x+y, z=w2→∂w∂z=2w, ∂x∂w=1 ∴∂x∂z=∂w∂z∂x∂w=2w⋅1=2(x+y)
이때, x와 y값을 알고 있어야 ∂x∂z의 값을 알 수 있다.
따라서, 컴퓨터는 역전파를 할 때, 각 노드의 텐서 값(위의 예에선 해당 노드의 x, y의 값)을 메모리에 기억해야한다.
3.1. 2-layer NN 역전파 예제

-
hr이 ol에 영향을 끼치는 정도는 Wrl(2)이다.
-
따라서 ol을 hr에 대해 미분하면 Wrl(2)만 살아남고 나머지는 사라지게 된다.
-
∂zk∂hr=σ′(zk)δrk에서 δrk는 크로네커 델타이다. 즉, r=k를 제외하고 사라지게 된다.
References






