확률론 맛보기

1. 확률론 in ML

---

• 딥러닝은 확률론 기반의 기계학습 이론에 바탕을 두고 있다.

• 기계학습에서 사용되는 손실함수(loss function)들의 작동 원리는 데이터 공간을 통계적으로 해석해 예측이 틀림 위험(risk)를 최소화하는 것이다.

회귀 분석에서는 $L_2$ 노름을 사용해 예측오차의 분산을 가장 최소화한다.

분류 문제에서는 교차엔트로피(cross-entropy)를 사용해 모델 예측의 불확실성을 최소화한다.

분산과 불확실성을 최소화하기 위해 측정을 할 때, 확률론과 통계학이 사용된다.

$\rightarrow$ 확률론과 통계학을 알아야 원리를 알 수 있다.

2. 확률변수와 확률분포

---

• 데이터 공간에서 데이터를 추출하는 분포인 확률분포 $\mathcal{D}$는 데이터의 초상화로 볼 수 있다.

• 확률변수는 일종의 함수로, 확률분포 $\mathcal{D}$의 종류에 따라 이산형(discrete)과 연속형(continuous)확률변수로 구분하게 된다.

• 이산형과 연속형이 아닌 확률변수도 있다.

• 이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 고려해 확률을 더해서 확률분포를 모델링한다.

• $P(X=x)$는 확률질량함수(PMF)로, 확률변수 X가 x값을 가질 확률이다.

• 연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도(density)위에서의 적분을 통해 확률분포를 모델링한다.

• $f_X(x) = \lim\limits_{h \to 0}\frac{F_X(x-h \ \le \ X \ \le \ x+h)}{2h}$는 확률밀도함수(PDF)로, 누적확률분포(CDF)의 변화율을 모델링한다. → 확률로 해석하면 안된다.

• 누적확률분포(CDF)는 $F_X(x) = P(X \le x) = \int_{-\infin}^xf_X(x)$이다.

데이터가 이산형인지 연속형인지 구분 후, 해당되는 방법에 따라 확률분포를 모델링해야한다.

즉, 데이터에 접근하는 방법에 따라 모델링하는 방법이 달라진다.

• 확률변수 $X, Y$가 있을 때, 결합 분포(joint distribution) $P(X,Y)$는 $\mathcal{D}$를 모델링한다.

• 데이터의 보는 관점에 따라 $X, Y$가 연속형/이산형이라도 결합분포는 이산형/연속형이 될 수 있다.

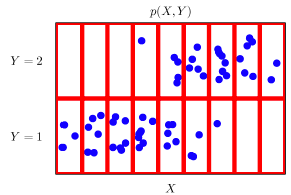
파란색 데이터의 확률분포 $\mathcal{D}$는 이론적으로 존재하지만 어떤 확률분포인지 사전에 알 수 없다.

결합분포 모델링을 통해 $\mathcal{D}$에 근사하는 확률분포를 구해야 한다.

• 위의 그림에서 확률변수 $X, Y$는 연속형이다. 하지만, 빨간색 선으로 나눠서 데이터를 바라본 결합분포는 이산형이다.

• 주변확률분포(marginal distribution) $P(X)$는 결합분포 $P(X,Y)$로 유도가능 하다.

3. 조건부확률 in ML

---

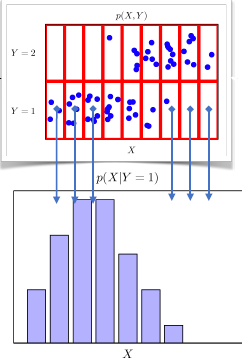
• 조건부확률 $P(Y|X)$은 데이터 공간에서 입력 $X$와 출력 $Y$ 사이의 관계를 모델링한다.

• 연속확률분포의 경우 $P(Y|X)$는 확률이 아니고 밀도로 해석한다는 것을 주의해야 한다.

3.1. 분류 문제

• 분류 문제에서 사용하는 선형모델과 소프트맥스 함수의 결합은 데이터에서 추출된 패턴을 기반으로 확률을 해석하는데 사용된다.

• softmax: $\sigma(\boldsymbol{W}\phi(\boldsymbol{X}) + \boldsymbol{b})$은 데이터 $\boldsymbol{X}$에서 추출된 특징패턴 $\phi(\boldsymbol{X})$과 가중치 행렬 $\boldsymbol{W}$을 통해 조건부확률 $P(Y|X)$을 계산한다.

• $P(Y|X)$는 $P(Y|\phi(\boldsymbol{X}))$와 같은 의미이다.

• 이것은 여러 층을 거쳐 추출된 특징: $\phi(\boldsymbol{X})$이 주어졌을 때, $Y$일 확률을 뜻한다.

• 특징패턴을 학습하기 위한 손실함수는 기계학습 문제와 모델에 의해 결정된다.

3.2. 회귀 문제

• 회귀 문제에서는 주로 연속형 확률변수를 다룬다.

• 확률밀도함수는 확률로 해석할 수 없기 때문에, 회귀 문제에서 $L_2$ 노름을 최소화하는 경우 조건부기대값 $\mathbb{E}[Y|X]$을 추정해야 한다.

• 경사하강법에서 $L_2$ 노름을 최소화하는 것은 다른 의미로 $\mathbb{E}[||Y-f(X)||_2]$가 0에 가깝도록 하는 것으로 볼 수 있다.

• $\mathbb{E}[||Y-f(X)||_2]$를 최소화하는 함수 $f(X)$는 조건부기댓값: $\mathbb{E}[Y|X]$과 일치한다.

• 증명은 아래의 reference를 참고하자.

• 즉, $\mathbb{E}[Y|X]$에 근사하도록 $f(X)$를 최적화하는 것이 경사하강법이다.

무조건 조건부기대값을 사용하지 않는다.

robust한 문제를 풀 때는 조건부기대값보다 중앙값(median)을 사용한다.

통계적 모형에서 원하는 목적에 따라 통계 추정량(estimator)을 선택 해야한다.

• 기대값(expectation)은 평균과 같은 의미이다. 기계학습에서는 데이터를 분석할 때 기대값을 여러 방면(분산, 공분산, $\dots$)에 사용한다.

4. 몬테카를로 샘플링(Monte Carlo Sampling)

---

• 기계학습 문제에서 데이터의 확률분포나 PMF 또는 PDF를 모르는 경우가 대부분이다.

• 확률분포를 모를 때, 데이터의 샘플링 방법을 알고 있다면 데이터를 통해 기대값에 근사하는 값을 구할 수 있다.

• 몬테카를로 샘플링에서 샘플링하는 방법은 i.i.d이어야 한다.

• 몬테카를로는 이산형이든 연속형이든 상관없이 성립한다.

• 몬테카를로 샘플링은 독립추출만 보장된다면 대수의 법칙(law of large)에 의해 수렴성을 보장한다.

• 몬테카를로 샘플링은 기계학습에서 다양하게 응용된다.

4.1. 예) $f(x) = e^{-x^2}$

• 함수 $f(x) = e^{-x^2}$ 상에서 적분값을 구해보자.

• $f(x)$의 적분을 해석적으로 구하는 것은 불가능하다.

• 몬테카를로 샘플링을 이용한다면 다음과 같다는 것을 알 수 있다.

• $f(x^{(i)})$는 높이 2는 밑변에 해당한다.

import numpy as np


def mc_int(fun, low, high, sample_size=100, repeat=10):
    # [-1, 1] 구간이므로 밑변에 해당하는 int_len의 값은 2이다.
    int_len = high-low
    stat = []
    for _ in range(repeat):
        # 균등분포로 sample_size만큼 [-1, 1] 구간의 x값을 추출한다.
        x = np.random.uniform(low=low, high=high, size=sample_size)

        # 추출된 x값으로 높이에 해당하는 함수 값을 계산한다.
        fun_x = fun(x)

        # 밑변과 높이를 곱해 넓이인 int_val을 계산한다.
        int_val = int_len * np.mean(fun_x)
        stat.append(int_val)

    # 구해진 통계량(넓이)를 평균내주면 실제 값과 거의 근사한다.
    return np.mean(stat), np.std(stat)


def f_x(x):
    return np.exp(-x**2)


print(mc_int(f_x, -1, 1, 10000, 100))
# 결과
# (1.4939731002894978, 0.003764717448739865)

• $\int^1_{-1}e^{-x^2}dx \approx 1.49364$이다.

• 함수 실행결과 $1.4939731 \ \ \pm \ \ 0.0037671$이므로 오차 범위 안에 참값이 있다.

• 적절한 sample size를 설정해줘야 근사하는 값이 나온다.

References

• 조건부 기댓값과 $L_2$ 노름의 최소화 관계 증명
• Proof: Conditional Expectation Minimizes MSE