통계학 맛보기

1. 확률분포와 모수

---

• 통계적 모델링은 주로 적절한 가정 위에서 확률분포를 추정하는 것이 목표이다.

• 해당 목표는 기계학습과 통계학이 공통적으로 추구하는 목표이다.

• 유한한 데이터만 관찰해서 모집단의 분포를 정확하게 알아낼 수 없으므로, 근사적으로 확률분포를 추정할 수 밖에 없다.

• 예측모형의 목적은 분포를 정확하게 맞추는 것보단, 데이터와 추정 방법의 불확실성을 고려해서 예측의 위험을 최소화하는 것이다.

• 데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후, 그 분포를 결정하는 모수(parameter) 추정을 통해, 데이터를 학습하는 방법을 모수적(parametric) 방법론이라 한다.

• 특정 확류룬포를 가정하기 않고, 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌면 비모수(nonparametric) 방법론이라 부른다.

• 기계학습의 많은 방법론은 비모수 방법론에 속한다.

1.1. 예) 확률분포 가정

• 우선 히스토르갬을 통해 모양을 관찰하여 확률분포를 가정한다.

데이터가 2개의 값만 가지는 경우 → 베르누이분포

데이터가 n개의 이산적인 값을 가지는 경우 → 카테고리분포

데이터가 [0, 1] 사이에서 값을 가지는 경우 → 베타분포

데이터가 0 이상의 값을 가지는 경우 → 감마분포, 로그정규분포 등

데이터가 $\mathbb{R}$ 전체에서 값을 가지는 경우 → 정규분포, 라플라스분포 등

• 위의 예시를 따라 기계적으로 확률분포를 가정하면 안 된다.

• 데이터를 생성하는 원리를 고려하여 확률분포를 가정해야 한다.

• 모수를 추정한 후에는, 각 분포마다 검정하는 방법들로 반드시 검정을 해야 한다.

1.2. 데이터로 모수 추정

• 데이터의 확률분포를 가정했다면 모수를 추정해볼 수 있다.

• 정규분포를 예시로 들어보자.

• 정규분포의 모수로는 평균 $\mu$ 과 분산 $\sigma^2$ 이 있다.

• 평균과 분산을 추정하는 통계량(statistic)은 다음과 같다.

• 표본평균: $\bar{X} = \frac{1}{N}\sum\limits_{i=1}^Nx_i$

• $\mathbb{E}[\bar{X}] = \mu$ → 표본평균의 기대값은 모집단의 평균과 같다.

• 표본분산: $S^2 = \frac{1}{N-1}\sum\limits_{i=1}^{N}(x_i - \bar{X})^2$

• $\mathbb{E}[S^2] = \sigma^2$ → 표본분산은 $N-1$로 나눠야 표본분산의 기대값이 모분산과 같아진다.

• 표본분산과 관련된 증명은 여기를 참고하자.

• 표본분산을 구할 때, $N$이 아니라 $N - 1$로 나누는 이유는 불편(unbiased)추정량으로 만들기 위해서이다.

• 편의(bias)은 추정량의 기대값 - 모수이다.

• 추정량의 기대값이 모수와 같아지는 것을 불편추정량이라 한다.

자유도와 불편추정량의 관계를 살펴보자.

자유도는 독립변수의 개수를 의미한다.

예) $x + y + z = 3$
→ 변수 2개만 주어지면 나머지 한개는 자동으로 결정되므로 자유도는 2이다.

표본분산은 표본의 평균이 a로 정해진 상황에서 구하게 된다. 표본평균이 a로 정해지는 순간 $x_1,\cdots,x_n$중에 $n-1$개가 정해지면, 나머지 하나는 종속적으로 정해지게 된다. 따라서 표본분산을 구할 때의 자유도는 $n - 1$이다.

표본분산을 불편추정량으로 만들기 위해 n-1로 나누게 되었는데, n-1로 나눠주고 보니 표본분산을 구하는 수식의 자유도와 같았다.라는 논리적 인과관계를 갖게된다.

2. 중심극한정리(CLT: Central Limit Theorem)

---

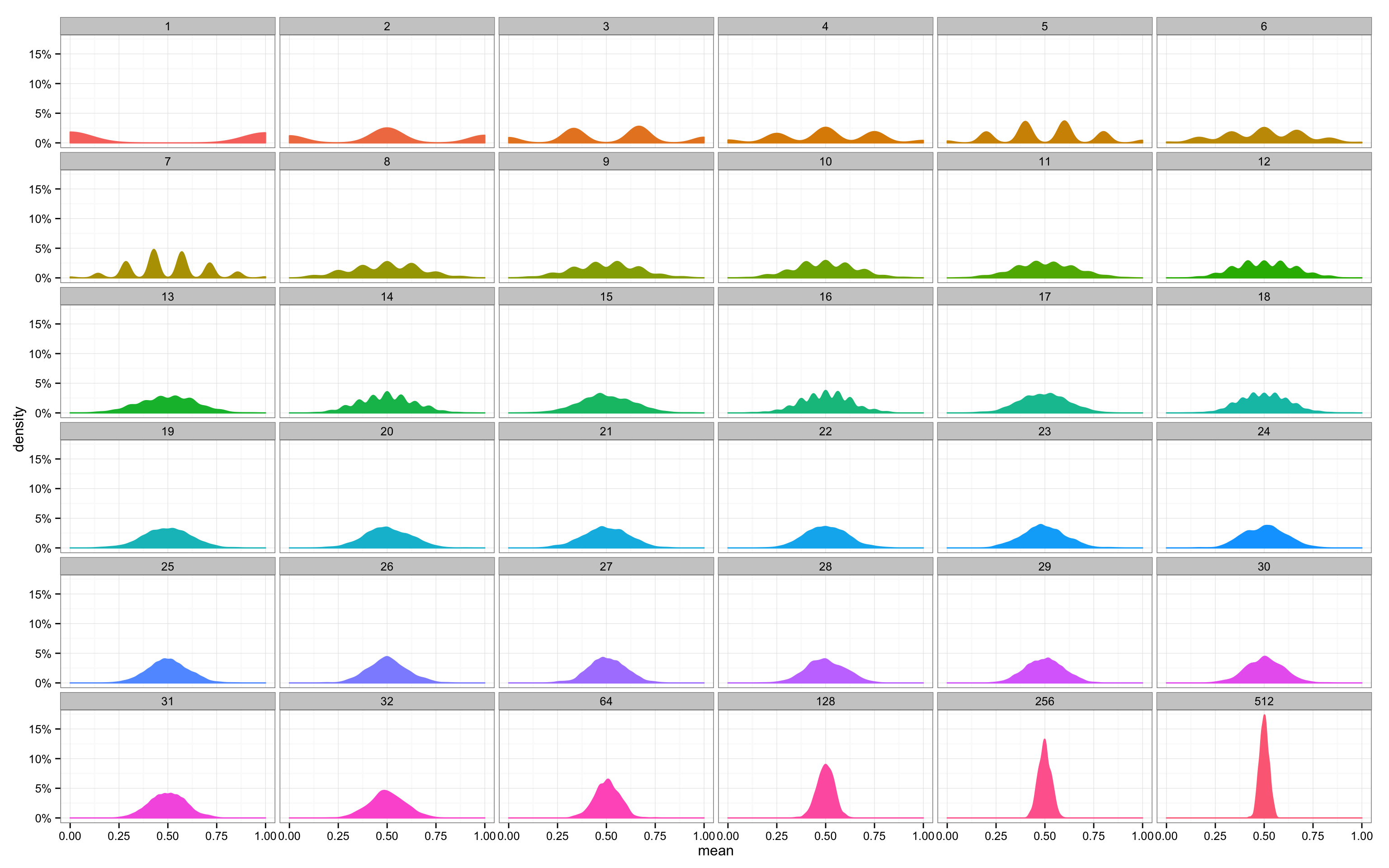
• 중심극한정리는 동일한 확률분포를 가진 독립 확률 변수 n개의 평균의 분포는 n이 적당히 크다면 정규분포에 가까워진다는 정리이다.

• 통계량의 확률분포를 표집분포(sampling distribution)라 부르며, 특히 표본평균의 표집분포는 $N$이 커질수록 정규분포 $\mathcal{N}(\mu, \sigma^2/N)$를 따른다.

• 이는 모집단이 정규분포가 아니라도 성립한다.

• 표본분포(sample distribution)과 표집분포(sampling distribution)은 다른 용어이다.

• 표본분포는 뽑힌 데이터의 통계량(표본평균, 표본분산, $\cdots$)이고, 표집분포는 이런 통계량들의 확률분포이다.

• 위의 사진은 이항분포에서 $N$에 따른 표본평균의 확률분포를 나타낸 것이다.

3. 최대가능도 추정법(MLE: Maximum Likelihood Estimation)

---

• 표본평균이나 표본분산은 중요한 통계량이지만, 확률분포마다 사용하는 모수가 다르다.

• 따라서, 확률분포를 추정하기 위한 적절한 통계량(표본평균, 표본분산, $\cdots$)이 달라지게 된다.

• 기계적으로 표본평균과 표본분산만으로 확률분포를 추정하면 안된다는 것이다.

• 이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나는 최대가능도추정법이다.

• 최대가능도추정법(또는 최대우도법, 이하 MLE)는 기계학습에서 여러모로 활용된다.

• $L(\theta|x)$와 $P(x|\theta)$는 관점의 차이다.

PMF 또는 PDF인 $P(x|\theta)$는 데이터의 확률분포를 알고 있을 때, 즉 모수 $\theta$를 알고 있을 때, $x$에 대한 함수이다.

$L(\theta|x)$는 가능도 함수로 주어진 데이터 $x$, 즉, 어떤 분포에 대해 이미 실현된 표본 값은 알고있지만, 모수 $\theta$를 모르고 있는 상황으로, 모수 $\theta$를 변수로 둔 함수이다.

• 모수 $\theta$를 변형시키면 가능도함수의 값이 변한다.

3.1. 가능도(likelihood) 함수

• 가능도(likelihood)는 확률분포의 모수 $\theta$가, 어떤 확률변수의 표집값 $x$ 와 일관되는 정도를 나타내는 값이다.

• 가능도 함수는 모수 $\theta$를 따르는 분포가 $x$를 관찰할 가능성으로 확률로 해석하면 안된다.

• 수치적으로 가능도를 계산하기 위해서, 각 데이터 샘플에서 후보 분포에 대한 높이(즉, likelihood)를 계산해 다 곱한 것(독립추출 가정)을 이용할 수 있다.

• 데이터 집합 행렬 $\boldsymbol{X}$의 행벡터 $\boldsymbol{x}_k$가 독립적으로 추출되었을 경우 가능도 함수는 PMF/PDF의 곱으로 표현할 수 있다.

• 위의 식을 가능도 함수이라고 하고 보통은 자연로그를 이용해 아래와 같이 로그가능도 함수(log-likelihood function) $\ log \ L(\theta|\boldsymbol{X})$를 이용한다.

• log 함수는 단조증가 함수이기 때문에 likelihood function와 log-likelihood function가 최대값을 갖게 해주는 정의역의 함수 입력값은 동일하다.

• 즉, 로그가능도를 최적화하는 모수 $\theta$는 가능도를 최적화하는 MLE가 된다.

로그가능도 사용하는 이유

1. 컴퓨터는 수억 단위를 계산할 때, 오차가 커진다. 만약 데이터가 독립일 경우, 곱셈을 덧셈으로 바꿀 수 있으므로 데이터가 커도 컴퓨터로 연산이 가능해진다.
2. 경사하강법으로 가능도를 최적화할 때, 미분 연산량이 $O(n^2)$에서 $O(n)$으로 줄어든다.
3. 대개의 손실함수의 경우 경사하강법을 사용하므로 목적식을 최소화 시킨다. 하지만, 로그 가능도의 경우 극대값을 찾게 된다. 그러므로 로그 가능도를 최소화시키는 목적식으로 변형하기 위해서, 음의 로그가능도(negative log-likelihood)를 최적화하게 된다.

3.2. 예제: 정규분포

$log \ L(\theta|\boldsymbol{x})$은 $-\mu^2 + \cdots$이므로 미분해서 0이되는 지점이 극대값이다.

$log\ 2\pi\sigma^2 = 2log\ \sigma + \cdots$

$log \ L(\theta|\boldsymbol{x})$는 $\sigma$에 대해 초반에는 $-\frac{c}{\sigma^2}$의 영향으로 $-\infin$에서 조금 증가하다가 결국에는 $log\ \sigma$의 영향으로 계속 감소하게 된다.

따라서 미분해서 0이되는 지점이 극대값이다.

표본분산의 불편추정량을 보장하는 통계량이다.

MLE는 가능도를 최대화하는 통계량으로 불편추정량을 보장하진 않는다. 하지만, 통계에서 말하는 consistence를 보장해주므로 MLE의 장점도 존재한다.

통계량을 하나만 사용할 필요는 없다.

3.3. 예제: 카테고리 분포

• 카테고리 분포는 여기를 참고하자.

• 카테고리 분포 $Cat(\boldsymbol{x}|\boldsymbol{p})$를 따르는 확률변수 $\boldsymbol{X}$로 부터 독립적인 표본 ${\boldsymbol{x}_1, \cdots, \boldsymbol{x}_N}$을 얻었을 때, MLE를 이용해 모수를 추정하자.
  
  

• $x_{n,k}$의 값은 0 또는 1이다.

• $\sum\limits_{n=1}^Nx_{n,k}$은 주어진 데이터에 대해서 $k$번째 원소 중 1인 값을 세는 것과 같다.

• 이를 $n_k$라고 하자. $n_k = \sum\limits_{n=1}^Nx_{n,k}$

• 오른쪽 제약을 만족하면서 왼쪽을 최대화하는 것이 목표이다.

• 라그랑주 승수법을 통해 최적화 문제를 풀어야 한다.

• 라그랑주 승수법은 여기를 참고하자.

• $\mathcal{L}$의 gradient vector가 0인 지점이 최적점이다.

• $\frac{n_k}{p_k} = \lambda$를 $\sum\limits_{k=1}^Kp_k = 1$에 대입하자.

MLE를 통해 기계학습 모델을 학습할 수 있다.

딥러닝 모델의 가중치를 $\theta = (\boldsymbol{W}^{(1)}, \cdots ,\boldsymbol{W}^{(L)})$라고 했을 때, 분류 문제에서 softmax vector는 카테고리분포의 모수 $(p_1, \cdots, p_K)$를 모델링한다.

one-hot vector로 표현한 정답레이블 $\boldsymbol{y} = (y_1,\cdots,y_K)$을 관찰데이터로 이용해 확률분포인 sofrmax vector의 log MLE를 최적화할 수 있다.

$\hat{\theta}_{MLE} = \underset{\theta}{argmax} \ \frac{1}{N}\sum\limits_{n=1}^N\sum\limits_{k=1}^K y_{n,k} \ log \ \{MLP_\theta(\boldsymbol{X}_n)\}_k$

위의 수식을 잘 기억하자.

4. 확률분포의 거리

---

• 기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터 에서 관찰되는 확률분포의 거리를 통해 유도된다.

• 즉, 손실함수는 정답 레이블 $y$의 확률분포와 예측 레이블 $\hat{y}$의 확률분포 거리를 통해 유도된다.

MLE를 사용 하는 모델 학습 방법론은 확률분포 거리를 최적화하는 것과 밀접한 관련이 있다.

• 데이터 공간에, 실제 값의 확률분포 $P(X)$와 예측 값의 확률분포 $Q(X)$가 있을 때, 두 확률분포 사이의 거리를 계산할 때 다음과 같은 함수들을 이용한다.

1. 총변동 거리(TV: Total Variation Distance)
2. 쿨백-라이블러 발산(KL: Kullback-Leibler Divergence)
3. 바슈타인 거리(Wasserstein Distance)

• 이번 포스트에선 쿨백-라이블러 발산(KL: Kullback-Leibler Divergence)에 대해서 알아볼 것이다.

• Entroy는 여기를 참고하자.

• Cross entropy와 쿨백-라이블러 발산(KL: Kullback-Leibler Divergence)는 밀접한 관계를 가지고 있기 때문에 같이 정리하겠다.

• Cross entropy는 두 확률 분포 $P, Q$ 사이의 차이를 측정하는 지표이다.

• Entropy는 하나의 확률 분포에 대한 측정 지표라면, Cross entropy는 두 확률 분포에 대한 측정 지표이다.

• Cross entropy의 수학적 정의는 아래와 같다.

• 첫번째 term은 true probability distribution p의 entropy를 의미한다.

• 두번째 term에서 확률분포 $P$와 $Q$의 정보량 차이가 정의되는데, 이것은 확률분포 $P, Q$의 차이를 나타내는 지표인 cross entropy의 핵심인 KL divergence이다.

• Cross entropy는 확률분포 $P, Q$의 차이를 나타내는 지표이고, KL divergence는 확률분포 $P$와 $Q$의 정보량 차이를 정의한다.

• optimization 동안 고정되어 있고, optimization 과정에서 approximation probability distribution $Q$가 바뀌며, 이에 따라 KL divergence이 바뀐다.

4.1. KL divergence

• 두 확률 분포 간의 KL divergence는 정보 이론적인 관점에서 보면 굉장히 다양한 해석이 가능하며, 놀라움의 표현이기도 하다.

• 두 확률 분포 $P, Q$가 가까웠다는 가정 하에, 만약 $P와 Q$가 가깝지 않다면 놀라운 일이며, 이 때 KL divergence는 높은 값을 갖게 되며, 반대로 가정대로 $P와 Q$가 가깝다면, 이는 놀랍지 않은 일이며 KL divergence도 낮은 값을 갖게 된다.

• Bayesian 관점에서 보면 KL divergence는 prior distribution $Q$에서 posterior distribution $P$로 이동할 때 얻어지는 information을 의미합니다.

• KL divergence의 표현은 likelihood ratio approach를 통해 나타낼 수 있습니다. likelihood ratio는 아래와 같이 쉽게 표현이 가능하다.

만약 어떠한 값 x가 임의의 분포로부터 sampling 되었을 때, likelihood ratio는 sample이 분포 $Q$보다 분포 $P$에서 나왔을 확률을 의미한다.

• $P$에서 나왔을 가능성이 높은 경우 LR은 1보다 큰 값을 갖고, 반대의 경우 1보다 작은 값을 갖는다.

• 독립적인 sample이 많이 있고, 이 모든 것들을 고려하여 likelihood function을 추정한다고 가정하면, 아래와 같이 LR을 나타낼 수 있습니다.

• 왼쪽 식을 ratio에서 $log$를 씌워주면 오른쪽과 같은 식을 얻을 수 있다. 이를 $log$ likelihood ratio라 부른다.

• $log$를 통해 likelihood ratio를 모종의 합으로 표현할 수 있게 된다. 이때, 각 sample들이 평균적으로 $Q$보다 $P$에서 나왔는지를 어떻게 정량화 하는지에 대해 알아보자.

• $log$ likelihood ratio에 기대값을 취하면 정량화 할 수 있다.

• $log$ likelihood ratio에 기대값을 취해준 값이 바로 KL divergence이다.

• 정리하면 KL divergence는 얼마나 sampled data가 $Q$ 분포 대신 $P$ 분포로부터 나왔는지를 나타내는 $log$ likelihood ratio의 기대값이다.

• 첫번째 term은 $P$ 분포에 대한 negative entropy를 의미한다.

• 두번째 term은 $P$ 분포에 대한 $Q$ 분포의 cross entropy를 의미한다.

두번째 term은 $P$ 분포에 의해 weighted 되어서 계산이된 $Q$ 분포의 entropy이다.

만약 $P$가 true distribution(실제 값의 확률분포)인 경우, KL divergence는 $Q$를 통해 표현할 때 손실된 정보의 양을 의미합니다.

추상적으로 생각해보면, 만약 $P$ 분포와 $Q$ 분포가 거의 같은 분포였다면, $P$를 $Q$로 나타내도 정보의 손실이 거의 발생하지 않을 것이다.

하지만 두 분포가 차이가 있었다면, $P$를 $Q$로 나타내는 과정에서 정보가 손실이 될 것이며, 이를 수식적으로 나타낸 값이 위의 식이다.

• KL divergence의 가장 중요한 특징은 교환법칙이 성립하지 않는다는 것이다.

$\mathbb{KL}(P||Q) \ne \mathbb{KL}(Q||P)$ → 부산-서울 최적 거리 $\ne$ 서울-부산 최적 거리

• 쿨백-라이블러 발산(KL: Kullback-Leibler Divergence)은 다음과 같이 정의된다.

• 이산확률변수 → $\mathbb{KL}(P||Q)=\sum\limits_{x\in\mathcal{X}}P(x)log\Big(\frac{P(x)}{Q(x)}\Big)$

• 연속확률변수 → $\mathbb{KL}(P||Q)=\int\limits_{x\in\mathcal{X}}P(x)log\Big(\frac{P(x)}{Q(x)}\Big)dx$

• 분류 문제에서 정답 레이블 $y$를 $P$, 모델 예측 $\hat{y}$를 $Q$라 두면, MLP에서 MLE의 가능도함수 $L(\theta|x)$는 쿨백-라이블러 발산의 -크로스 엔트로피 $\mathbb{E}_{x \sim P(X)}[logQ(x)]$ 와 같게 된다.

• 다시말해, MLP에서 MLE를 하는 것은 가능도함수의 최대값을 찾는 것이고, 쿨백-라이블러 발산의 크로스 엔트로피 $-\mathbb{E}_{x \sim P(X)}[logQ(x)]$ 의 최솟값을 찾는 것과 같다.

분류 문제에서 정답 레이블 $y$를 $P$, 모델 예측 $\hat{y}$를 $Q$라 두면, MLE은 쿨백-라이블러 발산을 최소화하는 것과 같다.

4.2. Cross entropy

• 위에서 정의했던 cross entropy 함수를 보면, $P$와 $Q$의 cross entropy는 true distribution $P$의 entropy와, $P$와 $Q$의 KL divergence의 합으로 정의가 되어있다.

• 이 두 term을 더하면 cross entropy를 아래와 같은 식으로 나타낼 수 있다.

• 주로 classification 문제를 풀 때 cross entropy loss를 사용한다.

예를 들어 0~9까지 손으로 쓴 숫자를 분류하는 MNIST classification에서 숫자 2의 경우 GT: ground truth은 {0, 0, 1, 0, 0, 0, 0, 0, 0, 0}이 된다.

Classification의 경우, NN(nerual network) 모델의 output layer에 보통 softmax layer를 마지막에 붙여줘서 output 값들이 0~1사이의 확률 값이 되고 다 더하면 1이 되도록 만들어준다.

NN 모델이 다음과 같이 예측하였다고 가정하다.

$Q$ = {0.01, 0.02, 0.75, 0.05, 0.02, 0.1, 0.001, 0.02, 0.009, 0.02}

neural network가 예측한 $Q$와 $P$의 차이를 측정하려면 어떻게 하면 좋을까? 두 확률 분포 간의 차이를 측정하는 지표인 cross entropy를 사용하면 된다.

$P$는 이미 one-hot encoding이 되어있기 때문에 2번째 값을 제외하면 모두 0 값을 갖게 된다.

이렇게 $P$가 one-hot encoding 되어있는 경우 하나를 제외하고 모두 0이므로, cross entropy는 시그마를 사용하지 않고 나타낼 수 있다.

$H(P,Q) = -1 \times log(Q(x_i))$

여기 예시에서 cross entropy loss는 $-log(0.75)=0.287$ 값을 갖는다.

$Q(x_i)$가 $1$에 가까워질수록 loss는 0으로 수렴할 것이다.

이렇게 cross entropy를 최소화하면서 neural network를 학습시키게 되는데, 이 cross entropy 식 자체가 $P$에 대한 Entropy와 $P, Q$간의 KL divergence의 합으로 구성이 되어있기 때문에 어떻게 보면 KL divergence를 최소화하는 것과 같다.

References

---

• 불편추정량
• 자유도와 불편추정량
• 중심극한정리
• 중심극한정리 시뮬레이션
• 최대우도법(MLE)
• 가능도
• An introduction to entropy, cross entropy and KL divergence in machine learning