[Time Series] 고전적인 분해법

온라인 Forecasting 교재 [Forecasting : Principles and Practice] 6장 3절을 참고하여 작성하였습니다.

6.3 고전적인 분해법

• 덧셈 분해와 곱셈 분해에 대한 더욱 자세한 설명
• 1920년대에 창안되었고, 다른 시계열 분해 방법의 기초가 된다.
• 가정 : 계절적인 성분이 매년 일정하다.
  • 주기 m 값을 계절성 지수(seasonal indices) 라고도 한다.

6.3.1 덧셈 분해

1단계

• 데이터에서 추세-주기 성분 T_hat_t 을 계산한다.
• m이 짝수?
  • 2×m MA를 사용하여 추세-주기 성분 T_hat_t 을 계산한다.
• m이 홀수?
  • m MA를 사용하여 추세-주기 성분 T_hat_t 을 계산한다.

2단계

• 데이터에서 추세-주기 성분을 제거한다. (계절성 + 나머지 만을 남긴다.)
  • y_t - T_hat_t

3단계

• 각 계절마다 계절성분 S_hat_t 을 측정한다.
• How? 추세를 제거한 값 → 해당 계절에 대한 평균
  • 월별 데이터에서 3월의 계절 성분을 측정하기 위해,
    데이터에서 추세를 제거한 뒤 모든 3월에 대한 평균을 계산한다.
  • 계산한 계절성분 값이 0 근처의 값으로 조정된다.

4단계

• 데이터 y_t에서 추세-주기 성분과 계절 성분을 빼서 나머지 성분을 계산한다.
  • R_hat_t = y_t − T_hat_t − S_hat_t

6.3.2 곱셈 분해

• 덧셈 분해법에서 뺄셈을 나눗셈으로

1단계

• 데이터에서 추세-주기 성분 T_hat_t 을 계산한다.
• m이 짝수?
  • 2×m MA를 사용하여 추세-주기 성분 T_hat_t 을 계산한다.
• m이 홀수?
  • m MA를 사용하여 추세-주기 성분 T_hat_t 을 계산한다.

2단계

• 데이터에서 추세-주기 성분을 제거한다. (계절성 + 나머지 만을 남긴다.)
  • y_t / T_hat_t

3단계

• 각 계절마다 계절성분 S_hat_t 을 측정한다.
• How? 추세를 제거한 값 → 해당 계절에 대한 평균
  • 월별 데이터에서 3월의 계절 성분을 측정하기 위해,
    데이터에서 추세를 제거한 뒤 모든 3월에 대한 평균을 계산한다.
  • 계산한 계절성분 값이 m 근처의 값으로 조정된다.

4단계

• 데이터 y_t에서 추세-주기 성분과 계절 성분을 나누어서 나머지 성분을 계산한다.
  - R_hat_t = y_t / (T_hat_t · S_hat_t)
  
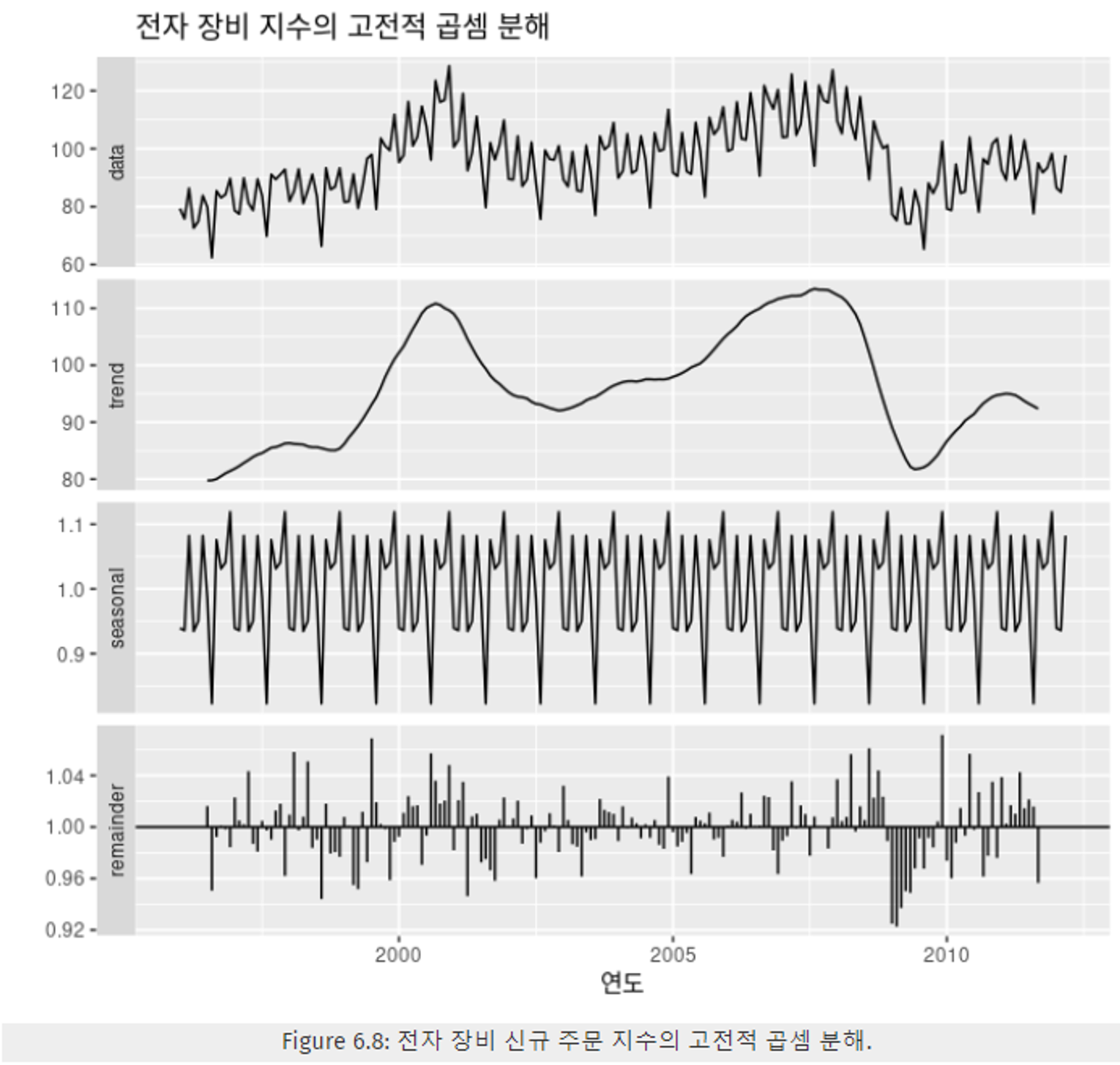
• 1보다 작은 나머지 값을 보면,
  추세-주기 성분의 일부가 나머지 성분으로 유출되어,
  나머지 성분에 안 좋은 영향을 준다.

6.3.3 고전적인 분해에 대한 첨언

• 여전히 널리 사용되고 있지만, 아래 문제들로 인해 주의를 해야하며, 더 나은 기법들을 사용한다.

1. 처음 몇 개와 마지막 몇 개의 관측값에 대한 추세 추정값을 얻을 수 없다. (이동평균을 사용해서)
   • 같은 기간에 대해 나머지 성분을 측정하는 것도 불가능
2. 추세-주기 측정은 데이터에 나타나는 급격한 증가나 감소를 과도하게 매끄럽게 한다.
3. 시간적으로 변하는 계절적인 변화를 다룰 수 없다.
   • 계절성분이 매년 반복된다는 것이 가정이기 때문에
4. 특이한 값을 다루기에 적절하지 않다.