[Time Series] 추세와 계절성의 강도를 측정하기

온라인 Forecasting 교재 [Forecasting : Principles and Practice] 6장 7절을 참고하여 작성하였습니다.

6.7 추세와 계절성의 강도를 측정하기

• 시계열 분해 표현
  $y_t=S_t+T_t+R_t$
  • T_t : 평활(smoothing)된 추세 성분
  • S_t : 계절성 성분
  • R_t : 나머지 성분
• 데이터에 시계열 개수가 많은 경우에 추세의 강도나 계절성의 강도를 통해 가장 강도가 강한 데이터를 찾는다.

6.7.1 추세의 강도

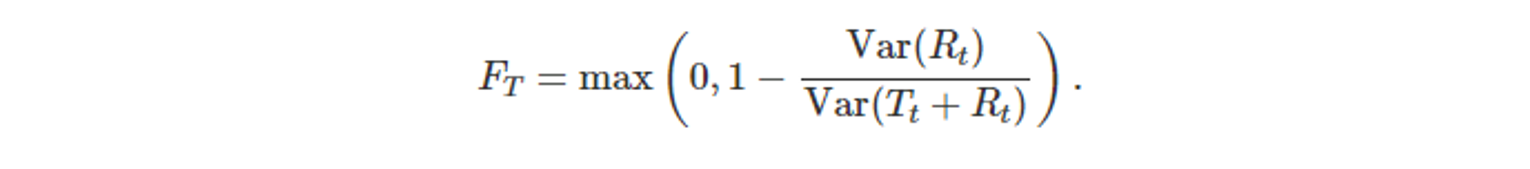
• 추세가 강하게 나타난다?
  • 계절성을 제외한 데이터(추세+나머지)가 나머지 성분보다 더 큰 변동성을 가진다.
  • Var(R_t) / Var(T_t+R_t) 가 상대적으로 작은 값이다. (T_t가 큰 값일 테니)
  • F_T ≈ 1
• 추세가 거의 없거나 아예 없다?
  • Var(R_t) / Var(T_t+R_t) 이 거의 1이 나와야 한다. (T_t 가 0에 가까울테니)
  • F_T ≈ 0
• 나머지 성분의 분산이 계절성을 제외한 데이터(추세+나머지)의 분산보다 크다?
  • 최소 값인 0이 된다.

6.7.2 계절성의 강도

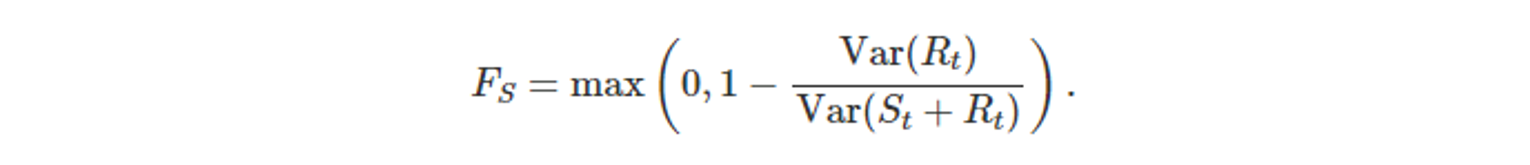
• 계절성이 강하다?
  • 추세-주기를 제외한 데이터(계절성+나머지)가 나머지 성분보다 더 큰 변동성을 가진다.
  • Var(R_t) / Var(S_t+R_t) 가 상대적으로 작은 값이다. (S_t가 큰 값일 테니)
  • F_S ≈ 1
• 계절성이 거의 없거나 아예 없다?
  • Var(R_t) / Var(S_t+R_t) 이 거의 1이 나와야 한다. (S_t 가 0에 가까울테니)
  • F_S ≈ 0
• 나머지 성분의 분산이 추세을 제외한 데이터(계절성+나머지)의 분산보다 크다?
  • 최소 값인 0이 된다.