[Time Series] 자기상관과 백색잡음

c_10.log·2023년 12월 14일

Time Series 📈

목록 보기

3/24

온라인 Forecasting 교재 [Forecasting : Principles and Practice] 2장 8, 9절을 참고하여 작성하였습니다.

autocorrelation
시계열의 시차 값(lagged values) 사이의 선형 관계를 측정
- 상관계수 : 두 변수 값 자체의 크기를 비교하여 선형 관계를 측정
시차 그래프(lag plot)를 통해 파악하는 자기상관 계수
- 예시
  r_1 : y_t와 y_t-1 사이의 관계를 측정하는 식
  r_2 : y_t와 y_t-2 사이의 관계를 측정하는 식
  t : 시계열의 길이
  k : 시점의 차이 $r_9= {((y_{10}-y_{avg})(y_{1}-y_{avg})+(y_{11}-y_{avg})(y_{2}-y_{avg})+(y_{12}-y_{avg})(y_{3}-y_{avg})+ ... + (y_{T}-y_{avg})(y_{n}-y_{avg}))}$ $/ \sum(y_{1,2, ... ,T}-y_{avg})$
일반화된 수식
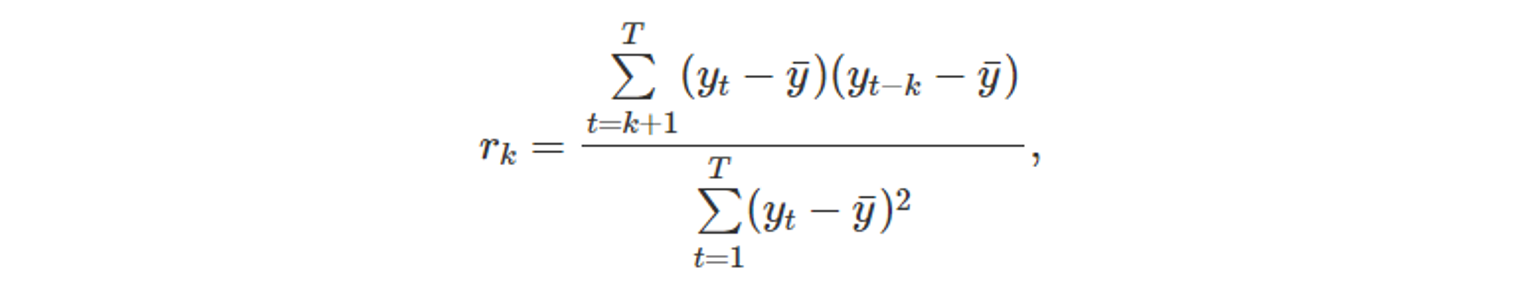
- 해석해보자면, k 만큼의 시점 차이가 존재하는 관측값 간의 관계를 구하는데, k 간격을 두고 모든 시점에 대한 자기상관 값을 산출함으로써,
  시차 값 사이의 선형 관계를 측정한다.
- 자기상관 계수 값이 클수록, 해당 값이 평균과 유의미한 차이가 난다는 것을 의미하고, 이는 시계열 데이터 측면에서 패턴이라고 인식할 수 있다.
맥주 생산량 데이터에 대한 처음 9개의 자기상관(autocorrelation) 계수

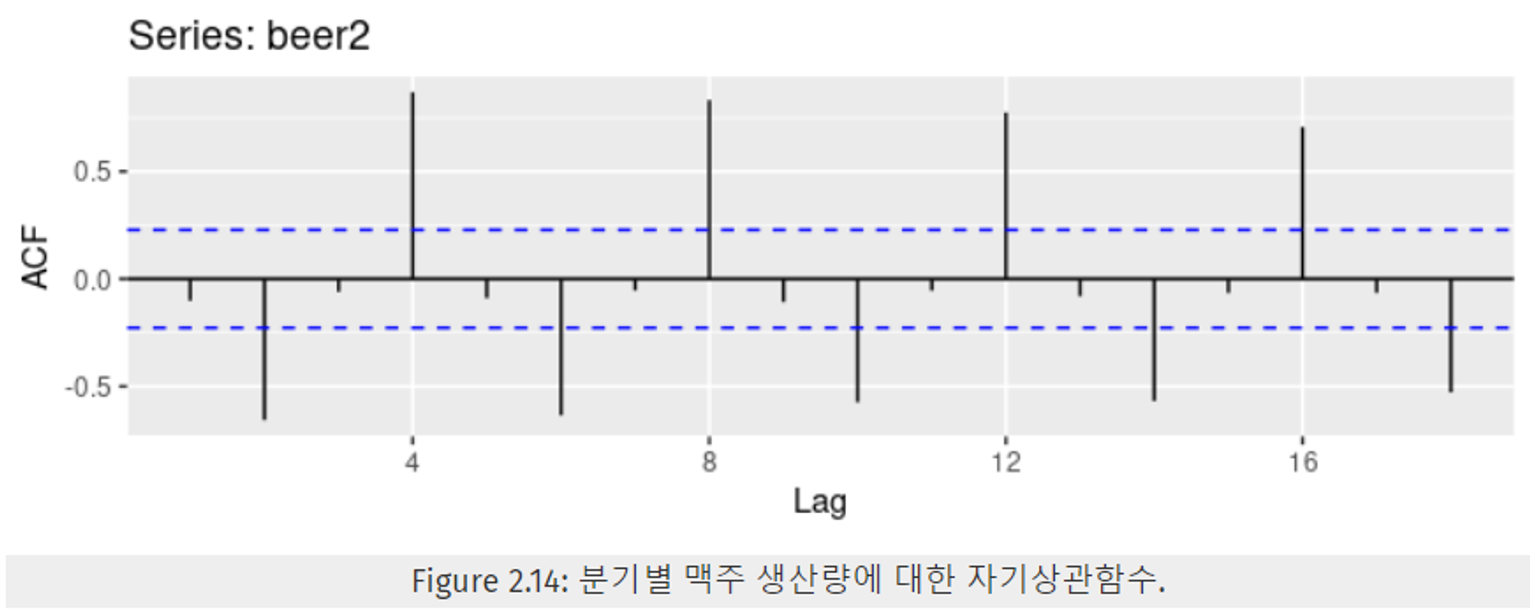
r_4가 가장 큰 양의 값이다.
- 이것은 데이터의 계절성 패턴이 존재한다는 것을 의미하고, 그 패턴의 시점 차이가 k=4 이므로, 4개의 분기마다 특정 패턴이 존재함을 알 수 있다.
- 고점은 4개의 분기마다 나타나고, 저점 역시 4개의 분기마다 나타난다는 것을 의미한다.
r_2는 가장 큰 음의 값이다.
- 저점이 고점 직후 2개 분기 마다 나타나는 경향을 가진다는 것을 의미한다.
파란 점선 : 상관계수가 0과 유의하게 다른지 아닌지를 나타낸다. 파란 점선보다 작으면 상관계수가 0에 가깝고, 이는 유의하지 않음을 나타낸다. 파란 점선은 ±2/√T 로 구할 수 있다.

시계열 데이터에 추세가 존재한다?
- 시차가 작은 경우, 자기상관 → 큰 양의 값을 가지는 경향
- Why? 시간적으로 가까운 관측치 → 관측값이 비슷한 경향을 가짐 → 비슷한 경향일수록 자기상관 값이 큰 양의 값을 가진다.
- 시계열의 ACF는 양의 값을 갖는 경향이 보이고,
- 시차가 증가함에 따라 ACF는 서서히 감소한다.
시계열 데이터에 계절성이 존재한다?
- 자기상관 → 계절성 시차의 경우 다른 시차의 경우보다 더 크게 나타난다.
시계열 데이터에 추세와 계절성이 모두 존재한다?
- 위 두 가지 특성이 모두 조합된다.
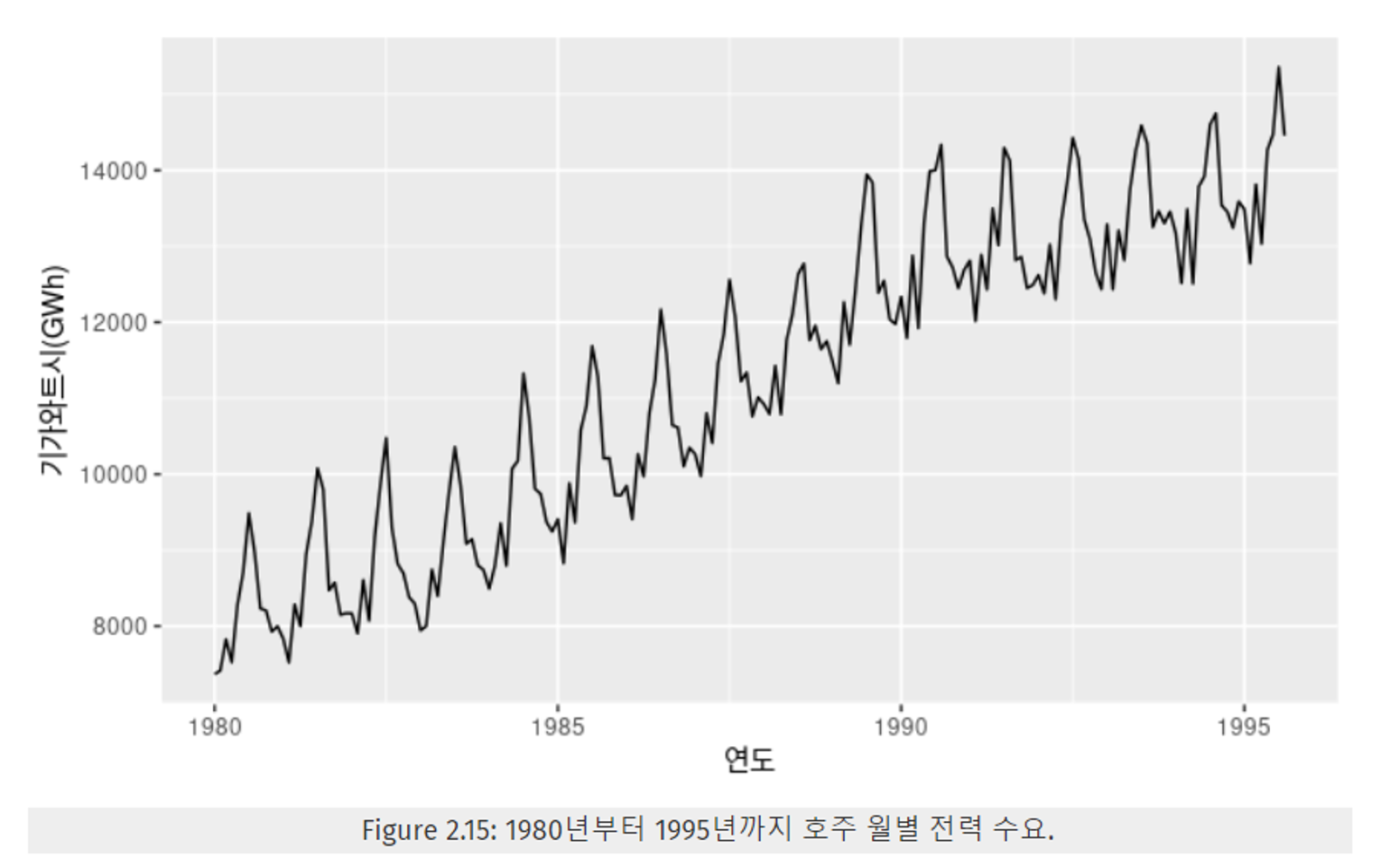
- 아래 Figure 2.15는 추세와 계절성이 모두 반영된 데이터이다.
- Figure 2.16은 데이터에 대한 ACF를 표현한 그래프이다.
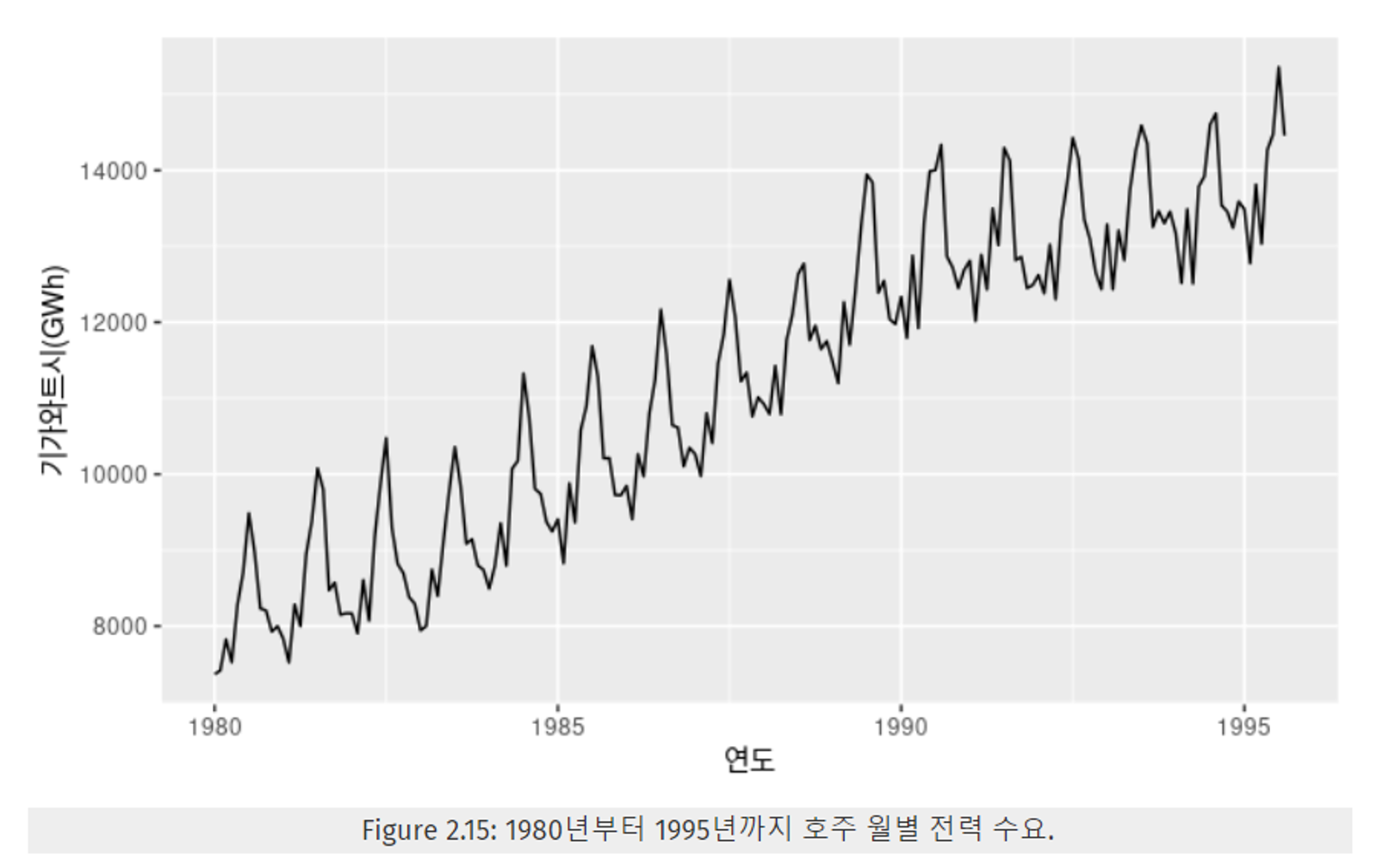
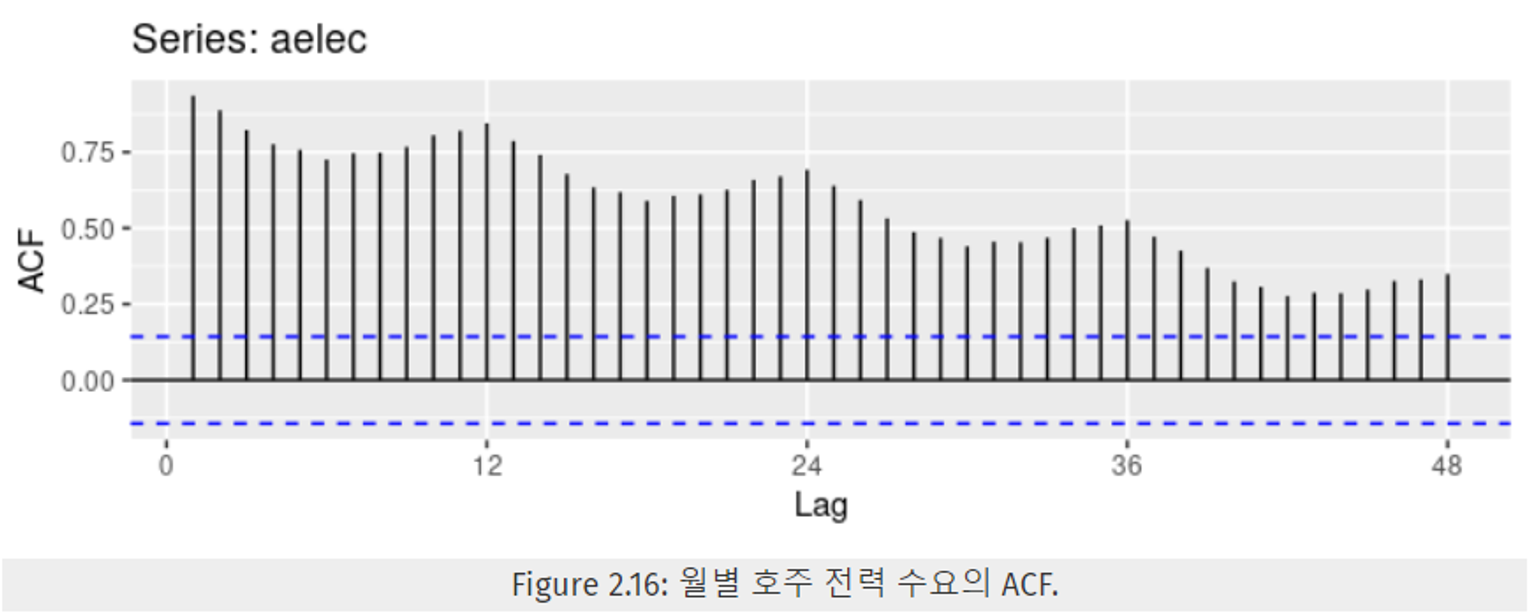
- Figure 2.16을 통해 파악할 수 있는 해당 시계열 데이터 특징
  - 추세로 인해, 시차값이 증가할수록 ACF값이 서서히 감소하는 모양을 보인다.
  - 계절성으로 인해, 물결 모양을 보인다.

white noise
자기상관(autocorrelation)이 없는 시계열을 부르는 말.
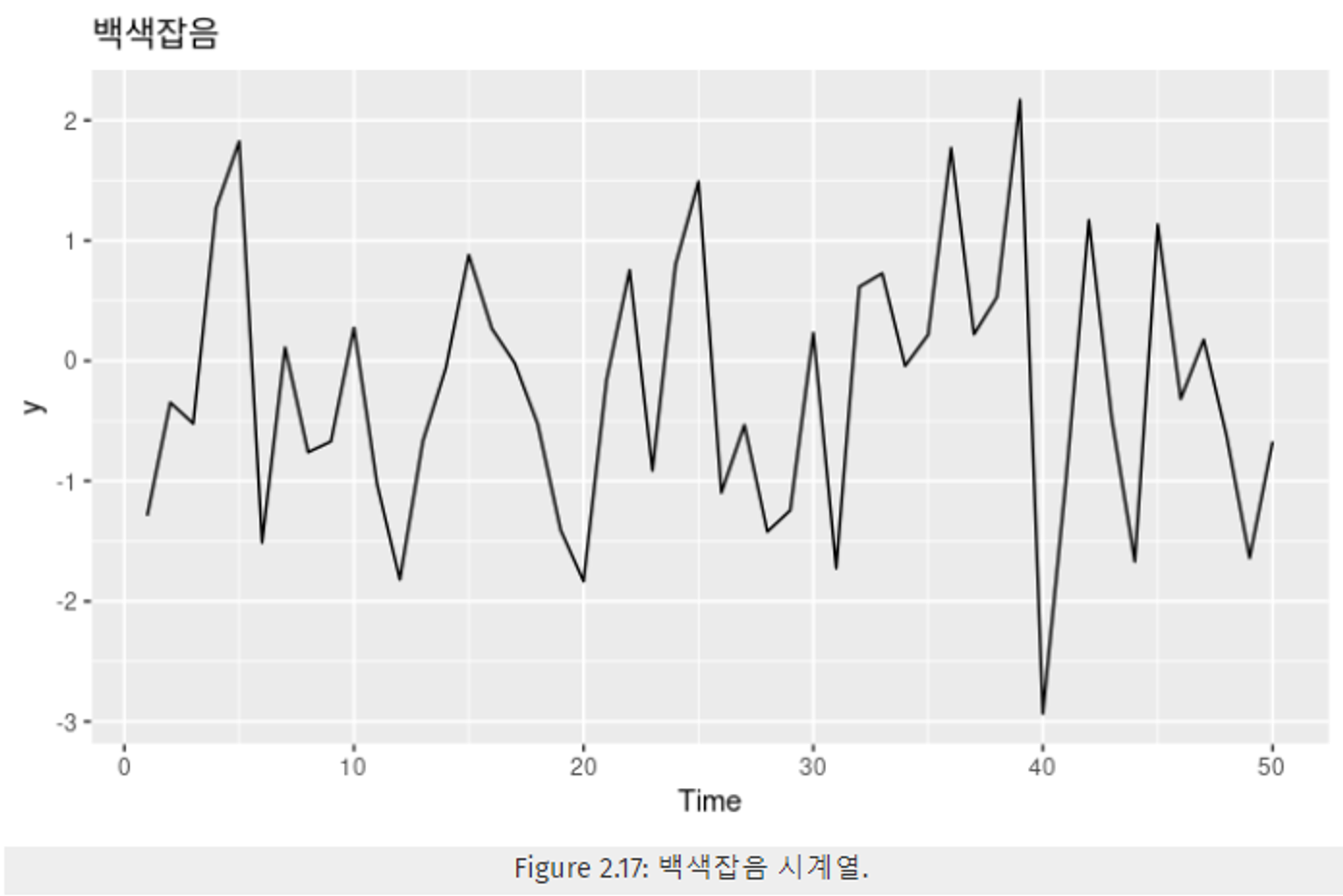
백색잡음 데이터의 기준?
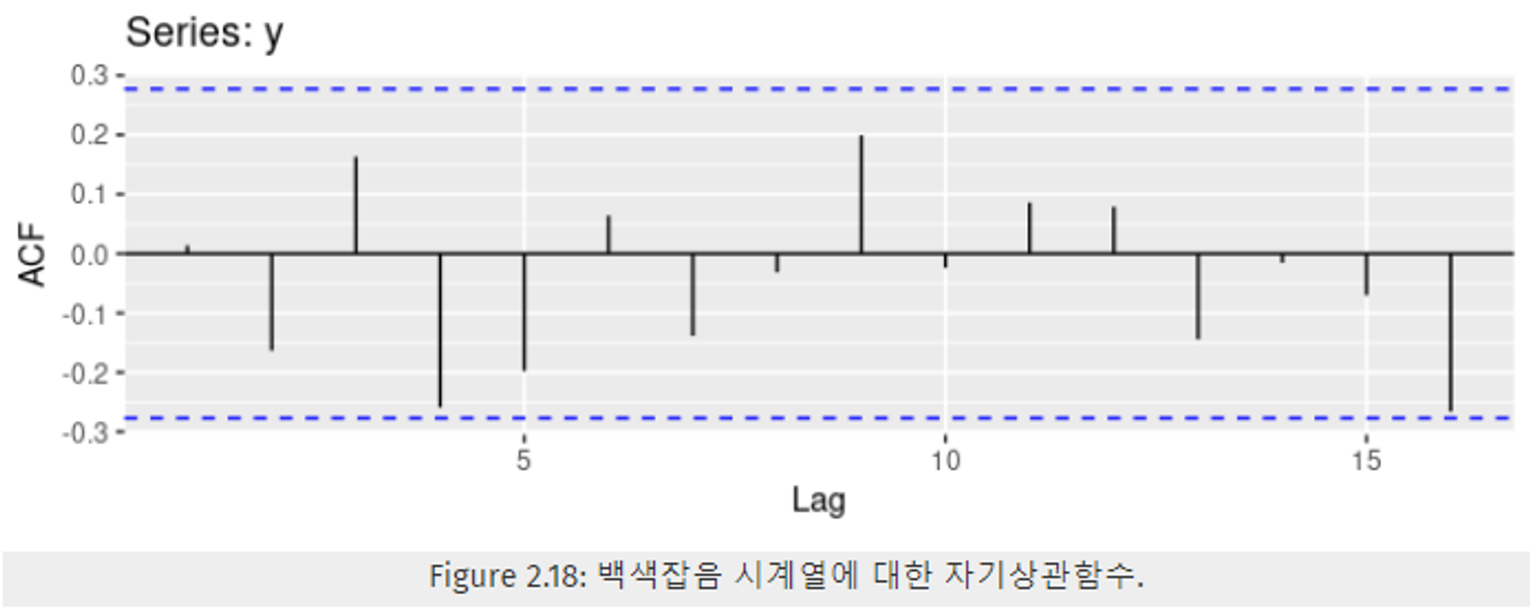
- 자기상관함수 값이 거의 0에 가까움을 알 수 있다. (무작위적 변동으로 인해 정확히 0이 아님)
  - 백색 잡음일 때는 뾰족한 막대의 95%가 ±2/√T 에 대부분 들어가고, 그래프에서는 파란 점선으로 표현한다. (T는 시계열의 길이)
Figure 2.18의 자기상관함수 값
- 꾸준히 증가하거나 감소하는 경향이 없다 → 추세 X
- 물결 모양이 없다 → 계절성 X