[Time Series] 선형 회귀 모델

온라인 Forecasting 교재 [Forecasting : Principles and Practice] 5장 1절을 참고하여 작성하였습니다.

5.1 선형 모델

가정

• 목표 예상변수 y와 예측변수 x 사이의 관계는 해당 선형 관계식을 만족한다.
• 오차 ε에 대한 가정은 아래와 같다.
  • 오차의 평균은 0이다. (그렇지 않으면 예측값이 편향된다.)
  • 오차는 자기상관관계가 없다. (그렇지 않으면 악용될 수 있는 정보가 더 많아진다.)
  • 오차는 예측변수 x와 상관관계가 없다. (그렇지 않으면 모델이 포함할 정보를 놓칠수도 있다.)
• 데이터 형태는 오차가 일정한 분산값 σ^2 을 가지는 정규 분포를 가진다. → 예측 구간을 쉽게 산출할 수 있다.
• 각 예측변수 x는 확률 변수가 아니다. (=통제된 상황에서 실험을 통해 얻은 값이다.)

5.1.1 단순 선형 회귀

• 하나의 y와 하나의 x 사이의 선형 관계

  • y_t (목표 예상 변수) : 예측 값
  • x_t (예측 변수) : 독립 변수
  • β_0 : 절편, β_1 : 기울기
  • ε_t : 오차
    $y_t = β_0 + β_1x_t + ε_t$

  

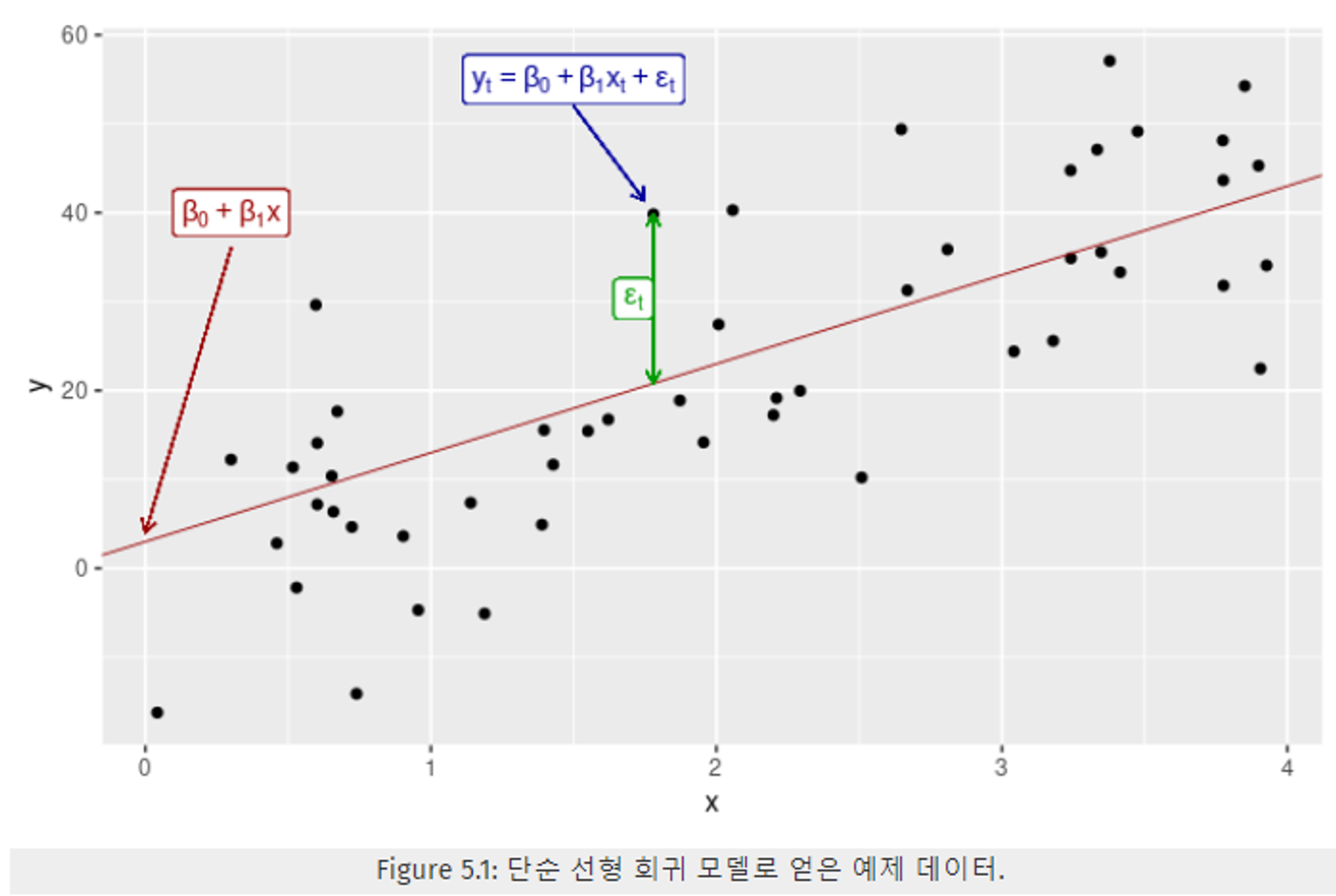
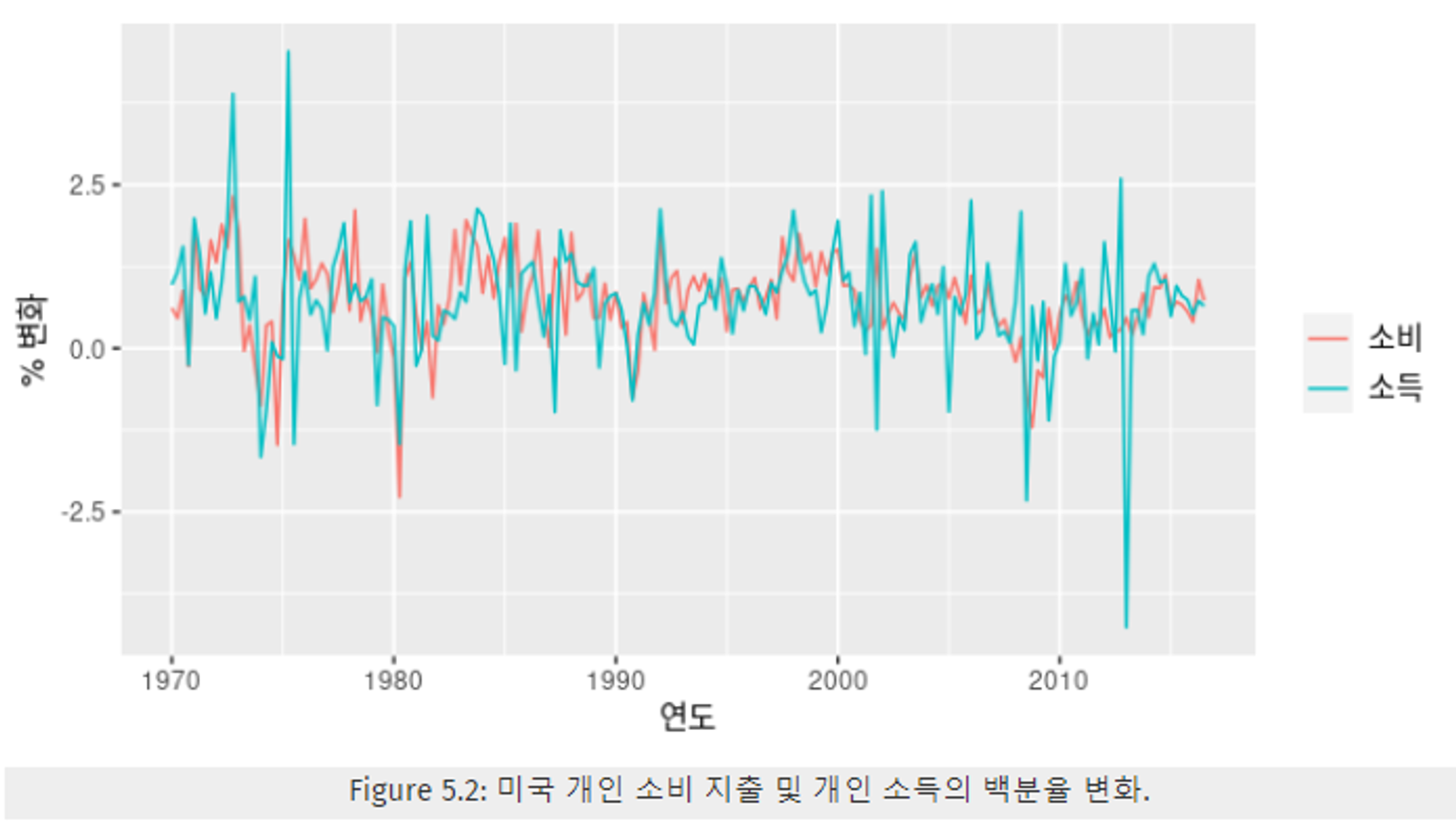
5.1.1 예제 : 미국 소비 지출

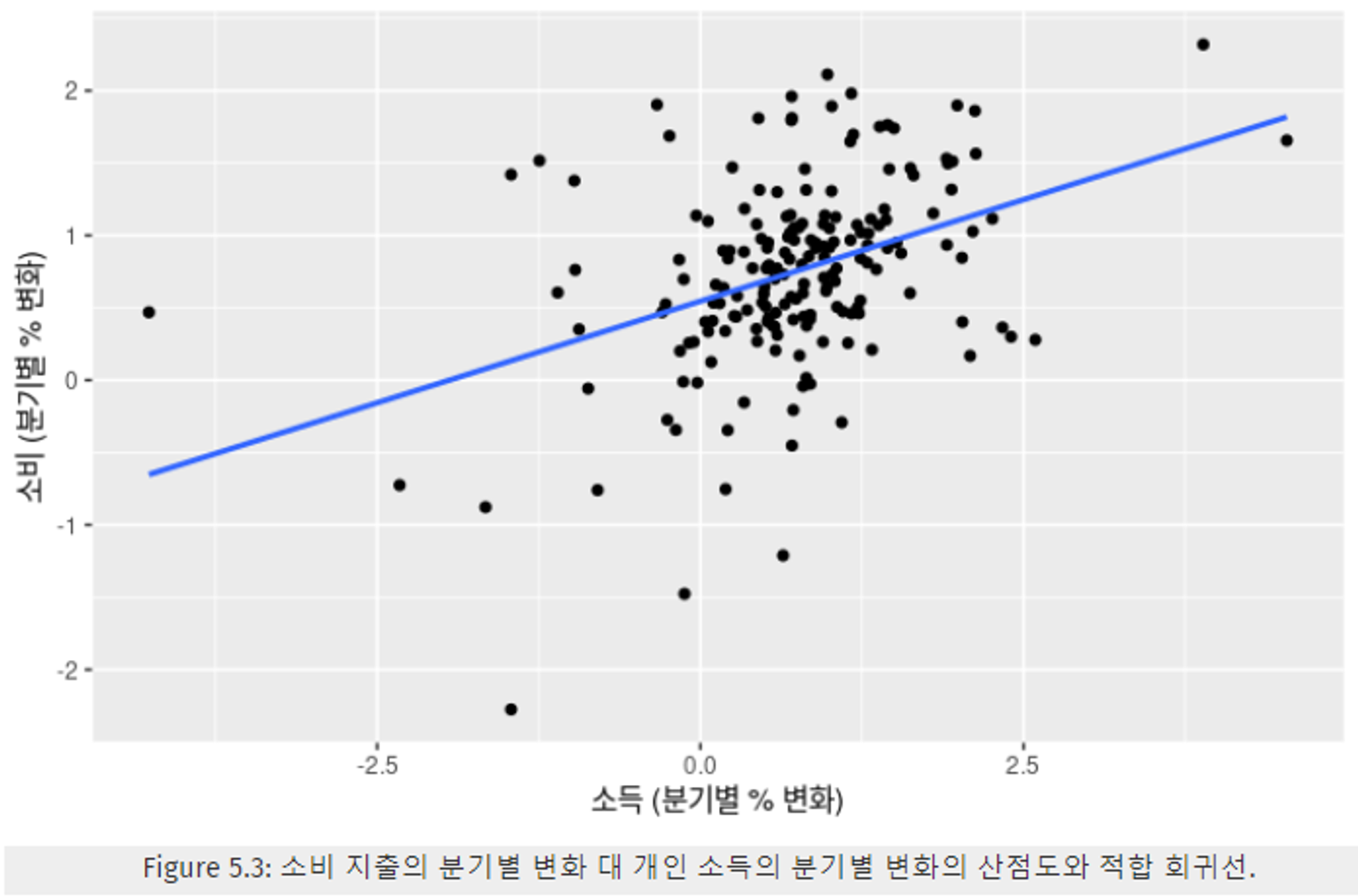
• Figure 5.3 : 소득 변화에 따른 소비 변화 → 산점도로 표현, 회귀선 추가
• 적합선
  $\hat y_t = 0.55 + 0.28x_t$
  • 위 식은 R 에서 tslm 함수를 통해 추정한 회귀식
  • 양의 기울기 → 소득과 소비 사이의 양의 관계를 반영하였다.
  • 기울기 +0.28 → x가 1만큼 증가할 때, y가 평균적으로 0.28씩 증가한다. (개인 소득이 1% 증가할 때, 개인 소비 지출이 평균적으로 0.28% 증가)
    
  • 모델에는 항상 y절편이 포함되어 있다고 가정한다.

5.1.2 다중 선형 회귀

• 두 개 이상의 x 가 있을 때의 모델
  • β_1, β_2, … , β_k : 각 예측 변수 x에 대한 계수, 효과를 나타낸다.
    • 이러한 계수를 예측 변수 x의 한계 효과(marginal effects)라고도 한다.
      $y_t = β_0 + β_1x_{1,t} + β_2x_{2,t} + ... + β_kx_{k,t} + ε_t$

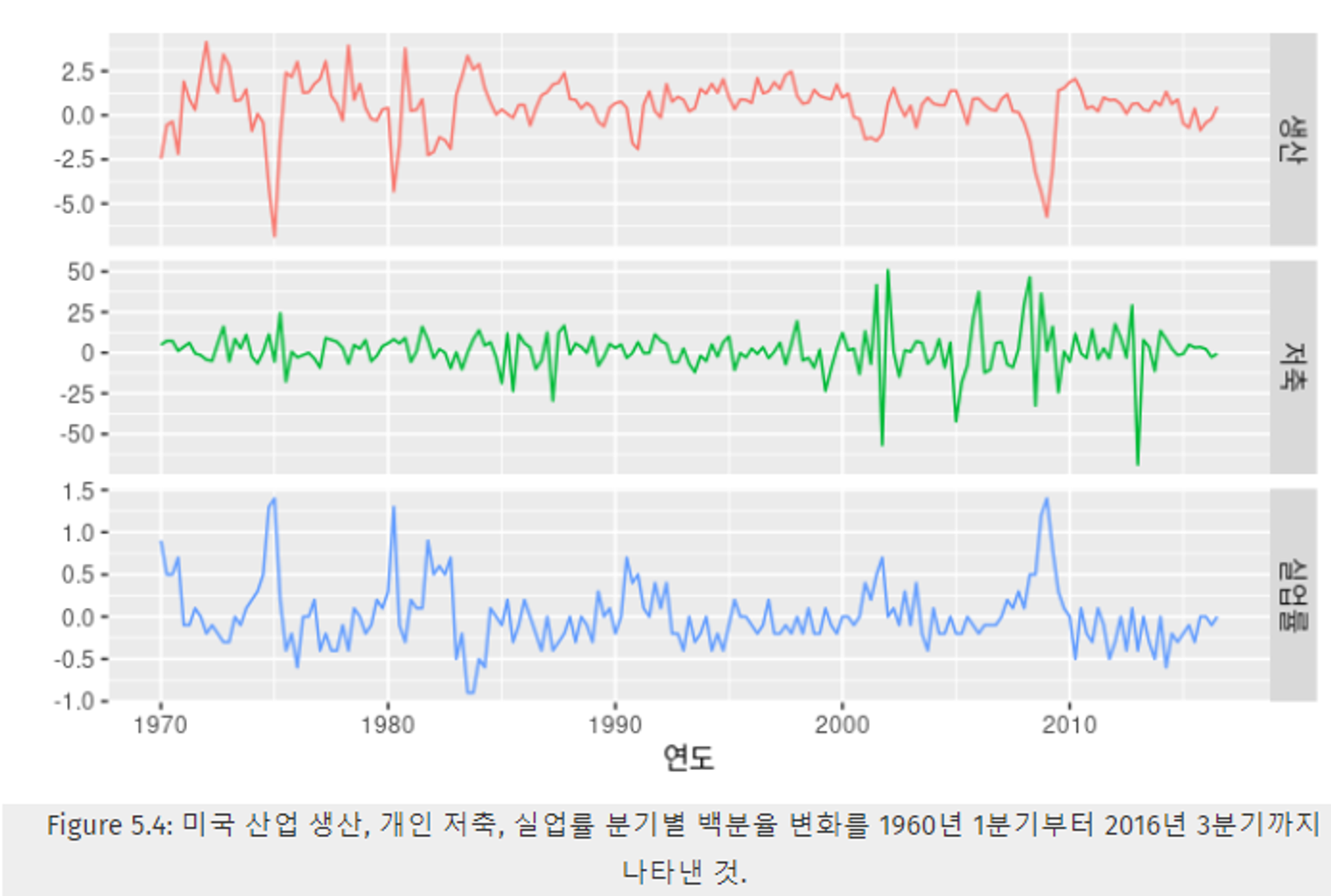
• Figure 5.4의 3가지 시계열 데이터를 추가하여, 총 4개의 예측 변수(소득, 생산, 저축, 실업률)와 1개의 목표 예상 변수(소비)로 이루어진 데이터 형태이다.

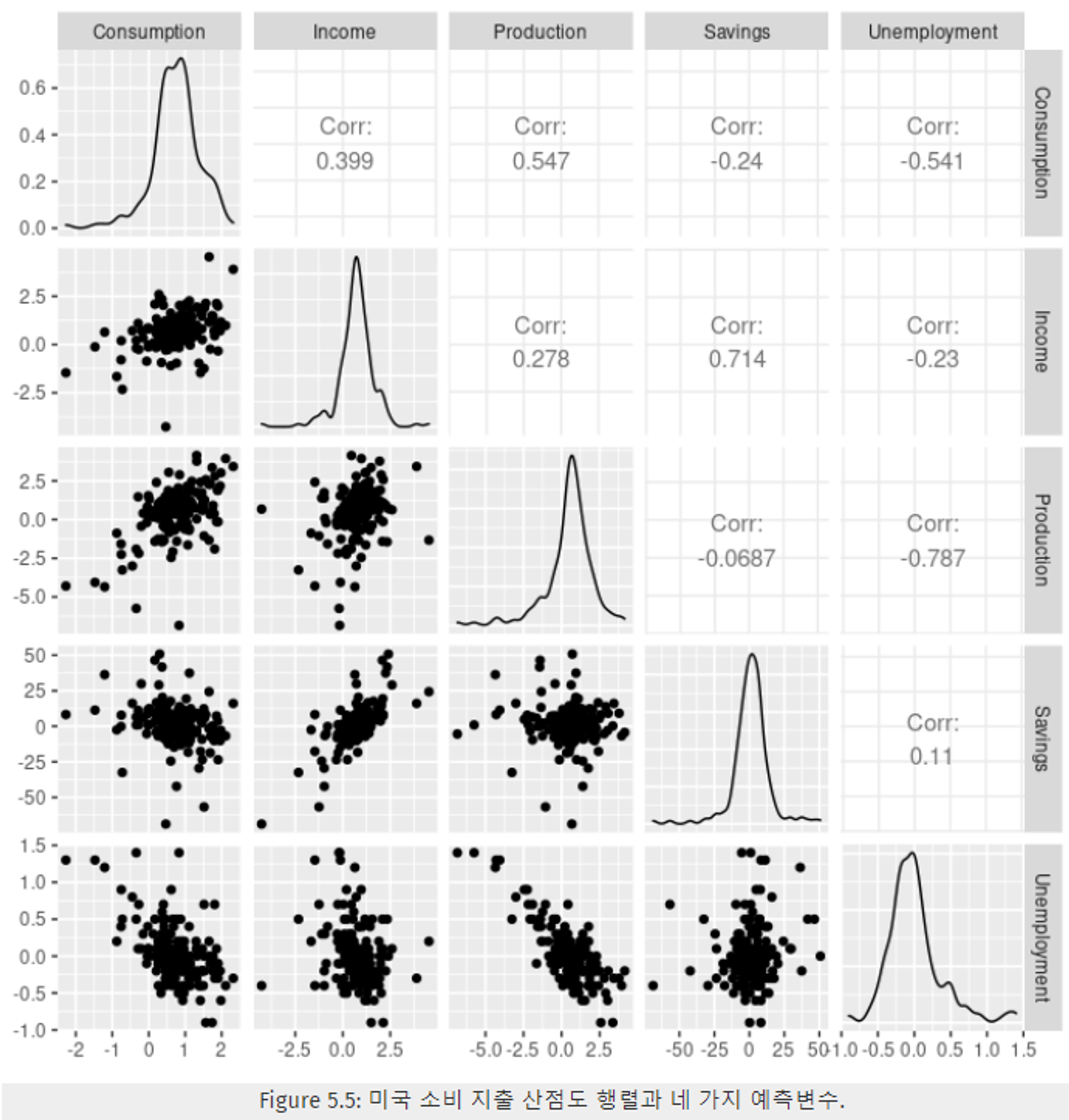
• 첫 번째 열을 보면, 목표 예상 변수(소비)에 대한 각 예측 변수 간 관계를 파악할 수 있다.
• Figure 5.5의 산점도 행렬을 통해 파악할 수 있는 점
  • 소득과 저축은 양의 상관관계를 보인다.
  • 생산과 실업률은 음의 상관관계를 보인다.

ㄟ(▔,▔)ㄏ 소득과 저축은 양의 상관관계를 보인다 ?

교재에서는 “소득과 산업 생산과의 양의 관계” 라고 하는데,
산점도 상에서 양의 관계인 것은 보이나,
상관계수에서도 알 수 있다시피 0.278로 큰 양의 관계는 아닌 것으로 보인다.

ㄟ(▔,▔)ㄏ 생산과 실업률은 음의 상관관계를 보인다 ?

교재에서는 “저축과 실업률과의 음의 관계”라고 하는데,
산점도 상에서 관계가 보이지 않으며,
상관계수에서도 0.11로 양의 값을 보이는 것을 알 수 있다.