[Time Series] 최소 제곱 추정

온라인 Forecasting 교재 [Forecasting : Principles and Practice] 5장 2절을 참고하여 작성하였습니다.

5.2 최소 제곱 추정

• 다중 선형 회귀에 등장하는 계수 β_0, β_1, … , β_k 를 추정하는 방법

• 구체적인 방법 : 오차의 제곱을 최소화하는 계수를 찾는다.

  

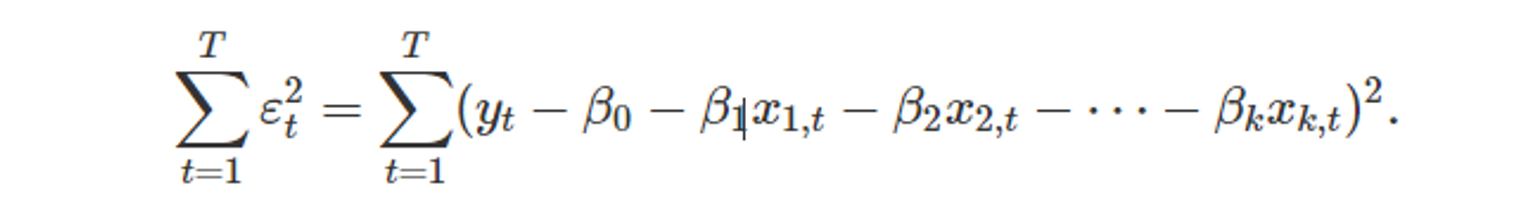
  • 오차는 실제값에서 예측값을 구하는 선형 회귀식을 뺀다.

• 이렇게 최소 제곱 추정을 통해 계수를 찾는 과정을 “학습”이나 “훈련” 이라고 부른다.

5.2 예제 : 미국 소비 지출

• 아래는 미국 소비 데이터를 다루는 다중 선형 회귀 모델이다.

  $y_t = β_0+β_1x_{1,t}+β_2x_{2,t}+β_3x_{3,t}+β_4x_{4,t}+ε_t$
  • y : 실제 개인 소비 지출의 변화율
  • x_1 : 실제 개인 가처분 소득의 변화율
  • x_2 : 산업 생산의 변화율
  • x_3 : 개인 저축의 변화율
  • x_4 : 실업률의 변화

• 용어 정리

  • β의 표준 오차
    비슷한 데이터에 대해 β계수를 반복적으로 추정하여 얻을 수 있는 표준 편차, β 계수의 불확실성을 의미한다.
  • t-value
    추정된 β 계수와 표준 오차의 비율
  • p-value
    관련 예측변수 x와 소비 y 사이에 실제 관계가 없는 경우,
    추정된 β 계수가 원래 값만큼 클 확률
    예측할 때 사용되지 않지만, 예측변수 x의 효과를 확인할 수 있다.

• 적합값

  • 회귀식에서 오차를 0으로 두어 y의 예측값을 얻을 수 있다.
    $\hat y_t = \hat β_0+\hat β_1x_{1,t}+\hat β_2x_{2,t}+\hat β_3x_{3,t}+...+\hat β_kx_{k,t}$
  • 이 때 t = 1, … , T 값을 대입하면 학습표본 안의 예측값 y_t를 얻게 되고, 이를 적합값이라 한다.
    • 주의! y에 대한 미래 예측값이 아닌, 모델 추정을 위해 보유하고 있는 데이터에 대한 예측값이다.
  • 내가 관측가능한 시점에 대한 데이터가 있는데, 모델을 해당 시점에 대해 예측한 값
    

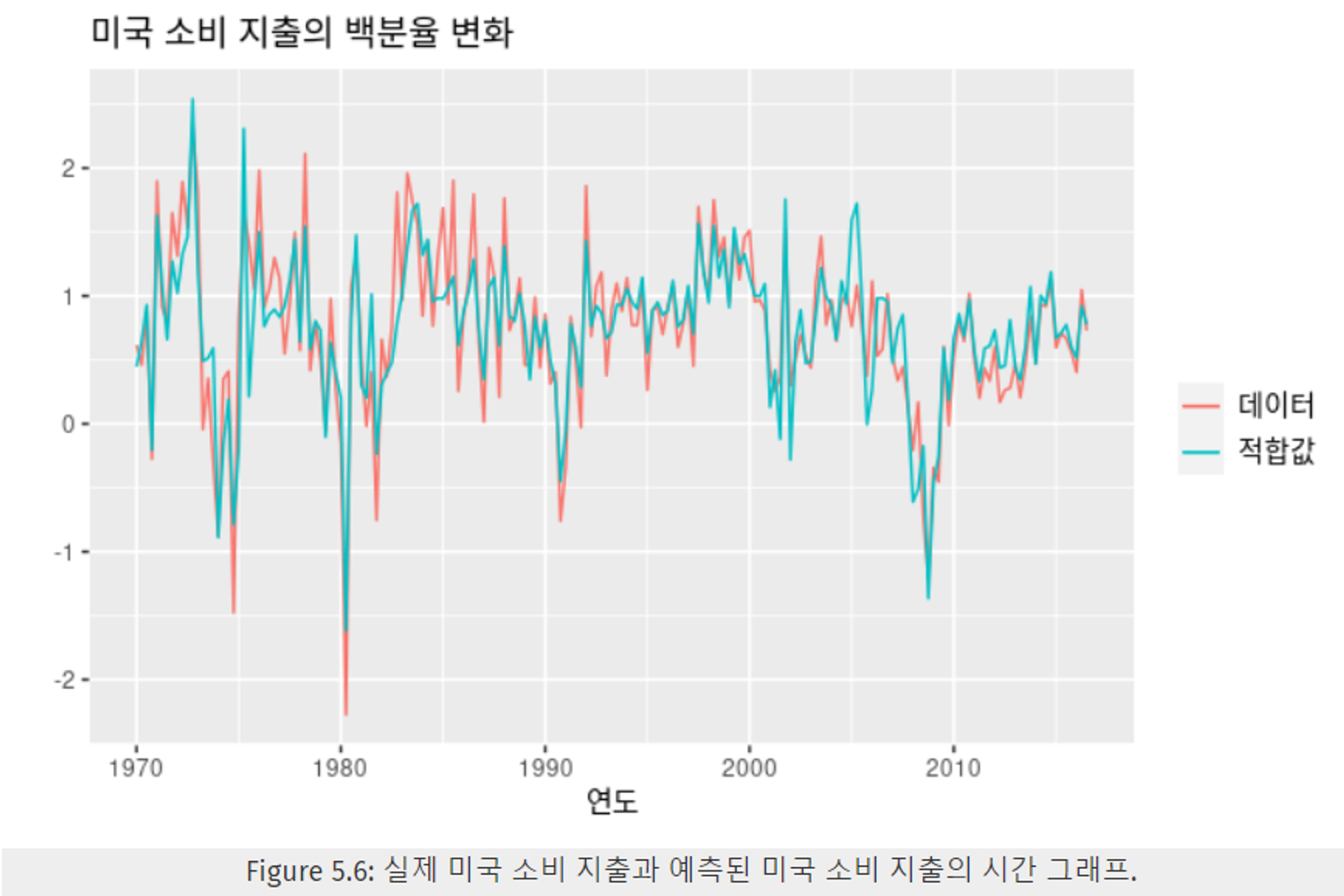
• Figure 5.6은 소비 지출 백분율 변화에 대한 실제 값과 적합 값(보유 데이터에 대한 예측값)을 시각화 한 것이다. 확인해보면, 적합 값이 실제 데이터를 꽤 잘 따라가는 모습이다.

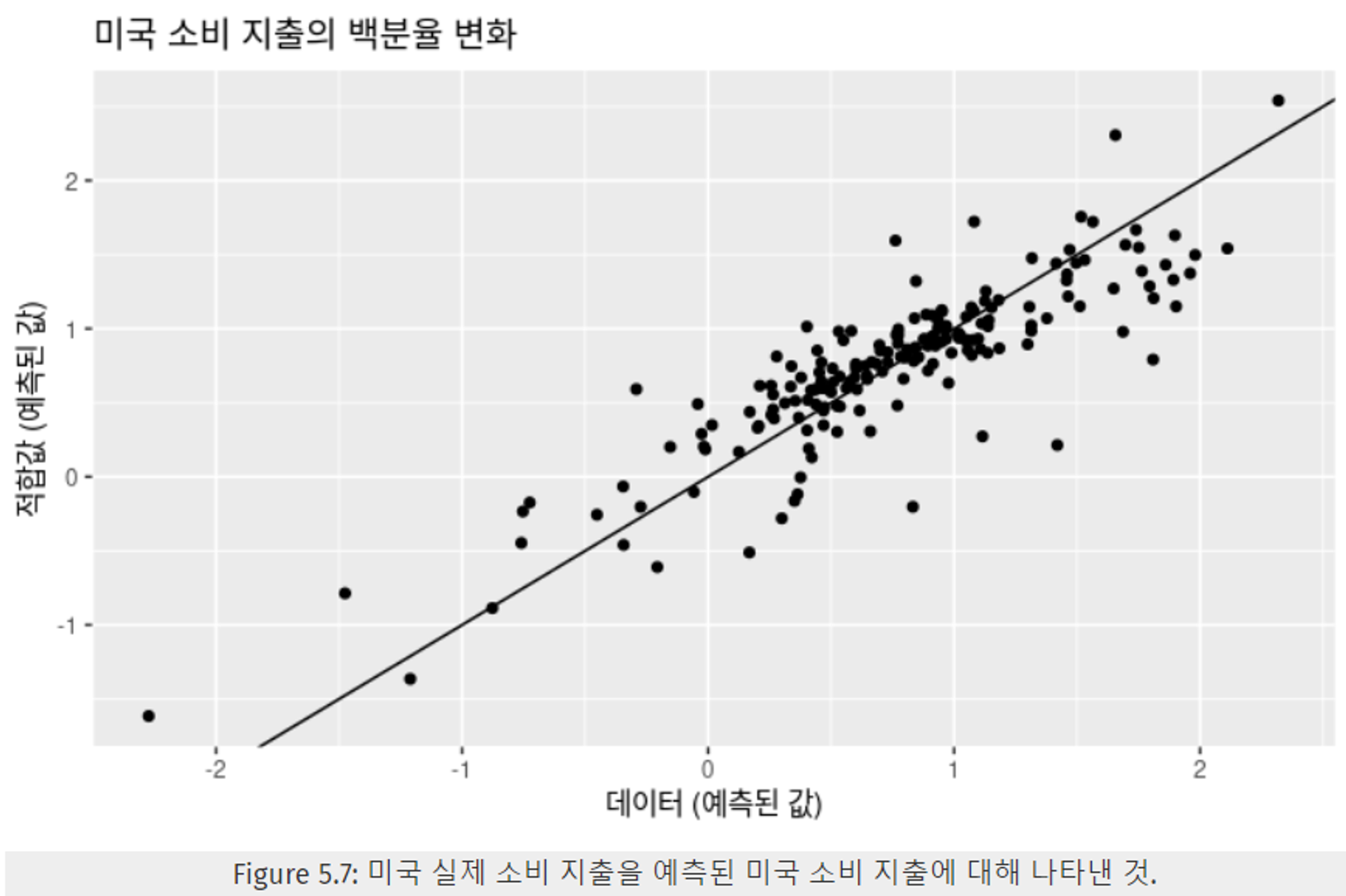
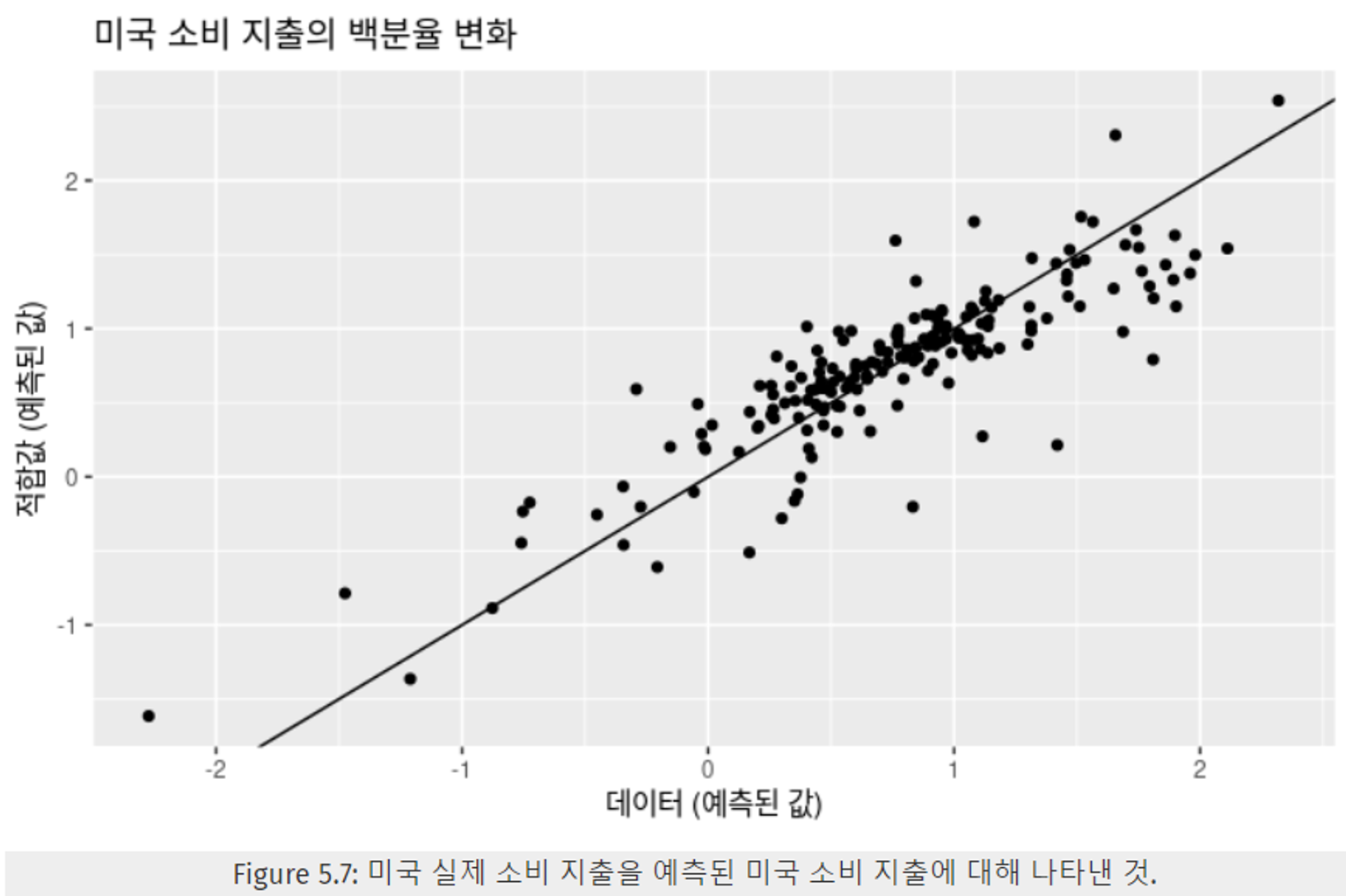
• Figure 5.7은 실제 데이터와 적합 값 간의 관계를 산점도로 표현한 것이다. 산점도 분포를 보면 강한 양의 상관관계를 보이고 있음을 알 수 있다. → 적합값이 실제 데이터와 유사하다는 것을 보여준다.

• 적합도

  • 선형 회귀 모델에 대한 성능 평가

    • 결정 계수(coefficient of determination)
    • R^2 score

    

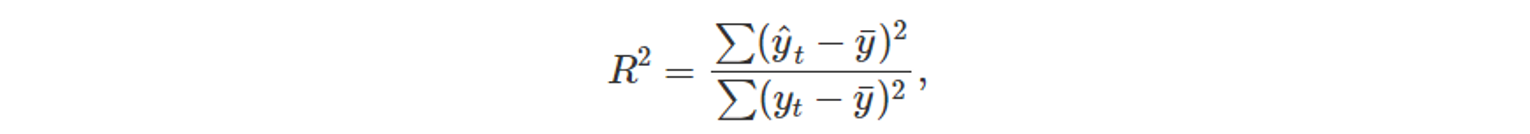
    • 관측한 y 값과 예측한 y_hat 사이의 상관 관계의 제곱
    • 회귀 모델로 설명되는 목표 예상변수 y의 변동 비율을 반영한다.
    • 성능이 좋다? R^2는 1에 가깝다. (0~1사이의 값을 가진다.)
    • 예측 작업에서 자주 사용되며, 예측 변수 x를 모델에 추가할 때, R^2 값은 줄어들지 않고, 과대적합으로 이어질 수 있다는 단점이 존재한다.

  • 미국 소비 데이터 예제

    • 소비 지출 값에 대한 실제 데이터 & 적합값 간 상관관계(correlation) r = 0.868, R^2 score = 0.754 (75.4%)
    • R^2 를 보면 75.4%의 변동을 설명하기 때문에 성능이 좋다고 할 수 있다. 예측변수 x를 추가한다면 소비 데이터의 변동을 더 잘 설명할 수 있고, R^2 는 올라갈 것이다.

5.2.1 회귀 분석의 표준 오차

• 모델 성능을 파악하는 또 다른 지표

  • 잔차 표준 오차 (residual standard error)

    

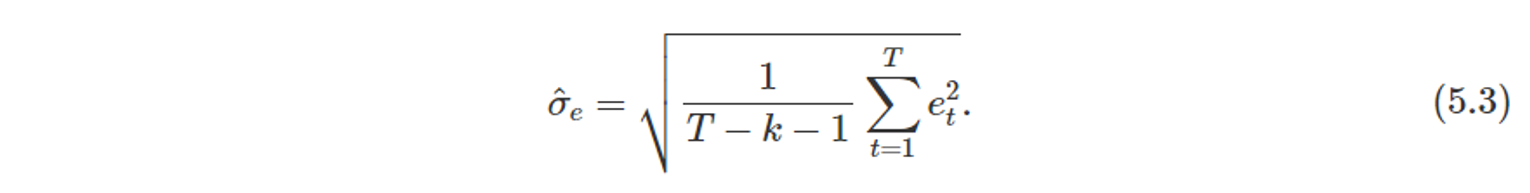
• k : 모델의 예측변수 x의 개수
• 잔차 계산
  • k+1개의 매개변수(예측변수 x의 개수 k개 + 절편 1개) 를 추정했기 때문에, 모든 시점의 오차에 대한 제곱 합을 {T - ( k+1 )}개로 나누어준다.
• 표준 오차는 모델의 평균 오차와 관련이 있고, 이 오차를 y의 표준편차와 비교하여 y의 표본 평균 및 모델 정확도를 파악할 수 있다. (이 오차와 표준편차가 유사하다면, 모델이 정확히 표현하고 있다는 것을 알 수 있다.)