온라인 Forecasting 교재 [Forecasting : Principles and Practice] 5장 5절을 참고하여 작성하였습니다.
5.5 예측변수 선택
- 회귀 모델에서 예측 변수는 무작정 많은 것이 좋지 않고, 가장 좋은 예측 변수 몇가지만 선택하는 전력이 필요하다.
- 부적합한 예측변수를 찾는 방법 → 유효하지 않은
- 특정한 예측변수 x를 목표 예상변수 y에 대해 그래프를 그렸을 때, 눈에 띄는 관계가 없는 경우 ( → 항상 유효한 방법은 X)
- 모든 예측변수 x에 대해 다중 선형 회귀 분석을 하여 p-value 가 0.05보다 큰 경우 ( → 2개 이상의 예측변수가 서로 관련 있을 때, p-value가 예상과 다르게 나올 수 있어서 유효한 방법은 X)
- 모델을 예측 용도로 사용할 때, 좋은 예측변수 x만을 고르는 것은 유용한 과정이지만,
예측변수 x에 대한 어떤 목표 예상변수 y의 효과를 확인할 때는 유용하지 않다. - 예측 정확도를 측정하는 5가지 지표를 아래 소개한다.
CV(fit.consMR) #> CV AIC AICc BIC AdjR2 #> 0.1163 -409.2980 -408.8314 -389.9114 0.7486- CV, AIC, AICc, BIC는 낮을수록, AdjR2는 높을수록 좋은 모델이다.
5.5.1 조정된 R^2
-
기존 R^2
- 모델이 과거 데이터를 얼마나 잘 설명하는지 측정하는 지표
- 미래 데이터를 얼마나 잘 예측하는지는 측정할 수 없다.
- 자유도(degree of freedom)를 허용하지 않는다.
- 예측변수를 추가하면, R^2는 (무조건?) 증가하는 경향을 보인다.
- R^2 score 만으로 모델 성능을 판단하면 안 된다.
-
과대 적합에 대한 판단이 되지 않기 때문에
⇒ 이러한 문제를 해결하기 위해 등장한 값이 조정된 R^2 이다.
-
- 모델이 과거 데이터를 얼마나 잘 설명하는지 측정하는 지표
-
조정된 R^2 (AdjR2)

-
T : 관측값의 개수
-
k : 예측변수의 개수
⇒ 이를 통해 예측변수 개수가 증가한다고 최종 R^2 값이 증가하는 문제를 방지할 수 있다.
-
-
너무 많은 예측변수를 선택하는 것이 문제가 될 수 있다.
그 기준을 조정된 R^2의 최대화로 삼는다면, 적절한 예측변수를 선택할 수 있다.
5.5.2 교차검증
- 방법
- t 시점의 관측값을 데이터 모음에서 제거하고, 나머지 데이터로 모델을 학습한다.
- t 시점을 제외한 데이터에 대한 오차를 t=1, … ,T에 대해 계산한다. (e^∗_1, … , e^*_T)
- 2번 과정을 통해 산출한 오차로 MSE를 계산하고, 이를 CV(Cross Validation)라 한다.
- CV가 가장 작은 모델이 좋은 모델이다.
5.5.3 아카이케의 정보 기준(Akaike’s Information Criterion; AIC)
- 교차검증(CV)와 밀접한 관련이 있다.
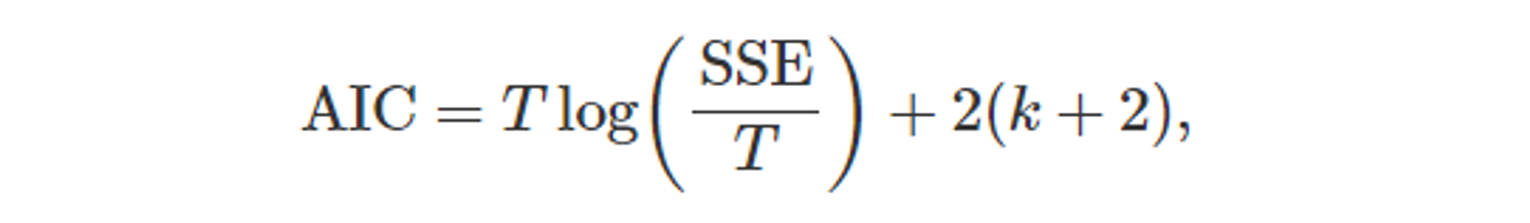
- T : 관측값의 개수
- k : 예측변수의 개수
- SSE : 오차의 제곱합
- 모델에 k개의 예측변수 개수와 추가로 절편, 오차가 있기 때문에
총 매개변수 개수은 (k+2)를 곱해준다.
- AIC 값이 최소인 모델이 좋은 모델이 된다.
- T 값이 충분히 크다면, AIC를 최소화 하는 것이 CV 를 최소화 하는 것과 같다.
5.5.4 수정된 아카이케의 정보 기준(AIC_c)
- T 값이 작다면 log(SSE/T) 값이 작아지기 때문에, AIC 값이 2(k+2)에 의존하게 된다. 결국 AIC 최소화를 위해 예측변수 x를 너무 많이 줄이게 된다.
- 이러한 문제를 해결하기 위해 AIC_c 가 등장하였다.
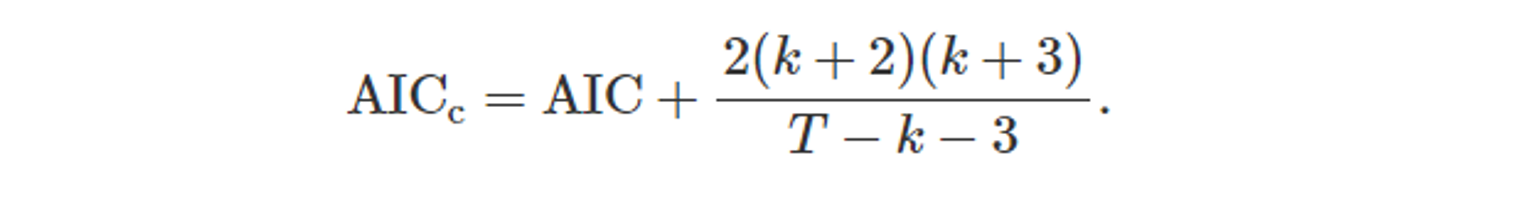
- 이러한 문제를 해결하기 위해 AIC_c 가 등장하였다.
- AIC와 마찬가지로 AIC_c 값이 최소인 모델이 좋은 모델이 된다.
5.5.5 슈바르츠의 베이지안 정보 기준(SBIC)
- Schwarzd Bayesian Information Crieterion(SBIC), BIC, SC
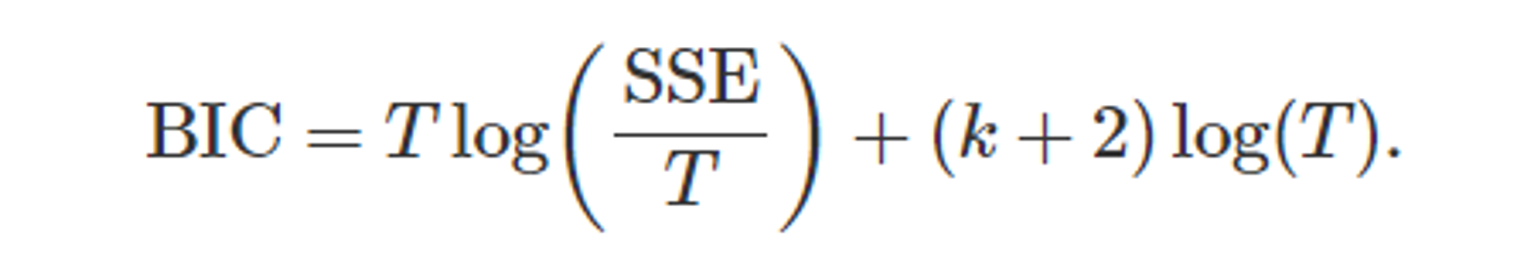
- AIC보다 더 적은 수의 항을 고려한 것과 같다.
- BIC가 매개변수 수에 더 큰 제한을 주기 때문이다.
- 식을 AIC와 비교해보면, AIC에서 2를 곱하던 값이, BIC에서는 log(T)를 곱한다. 그렇기 때문에 T를 최소화 하는 것도 중요한 요소이다.
- BIC가 매개변수 수에 더 큰 제한을 주기 때문이다.
- AIC와 마찬가지로 SBIC 값이 최소인 모델이 좋은 모델이 된다.
- 큰 T값에 대해, BIC를 최소화하는 것은 v=T[1−1/(log(T)−1)]일 때,
v개 관측치 제거법 교차 검증하는 것과 비슷합니다.
5.5.6 어떤 지표를 사용해야 하는지?
- R^2가 널리 사용되고, 오래되었다.
- 하지만, 예측변수의 개수가 많을수록 성능이 좋게 나와서 예측 작업에 가장 적합하진 않다.
- 충분한 데이터가 있다면, SBIC 값이 좋은 모델을 정하는 가장 좋은 기준이 될 것이다.
-
하지만, 이 또한, 가장 좋은 예측 성능을 보일 것이라는 보장이 없다.

-
- 결론 : 1) 한 가지 지표만 볼 수 없다. 2) 예측 성능이 좋은 것을 찾기 위해서 AIC_c, AIC, CV 를 주로 사용한다.
5.5.7 예시 : 미국 소비
-
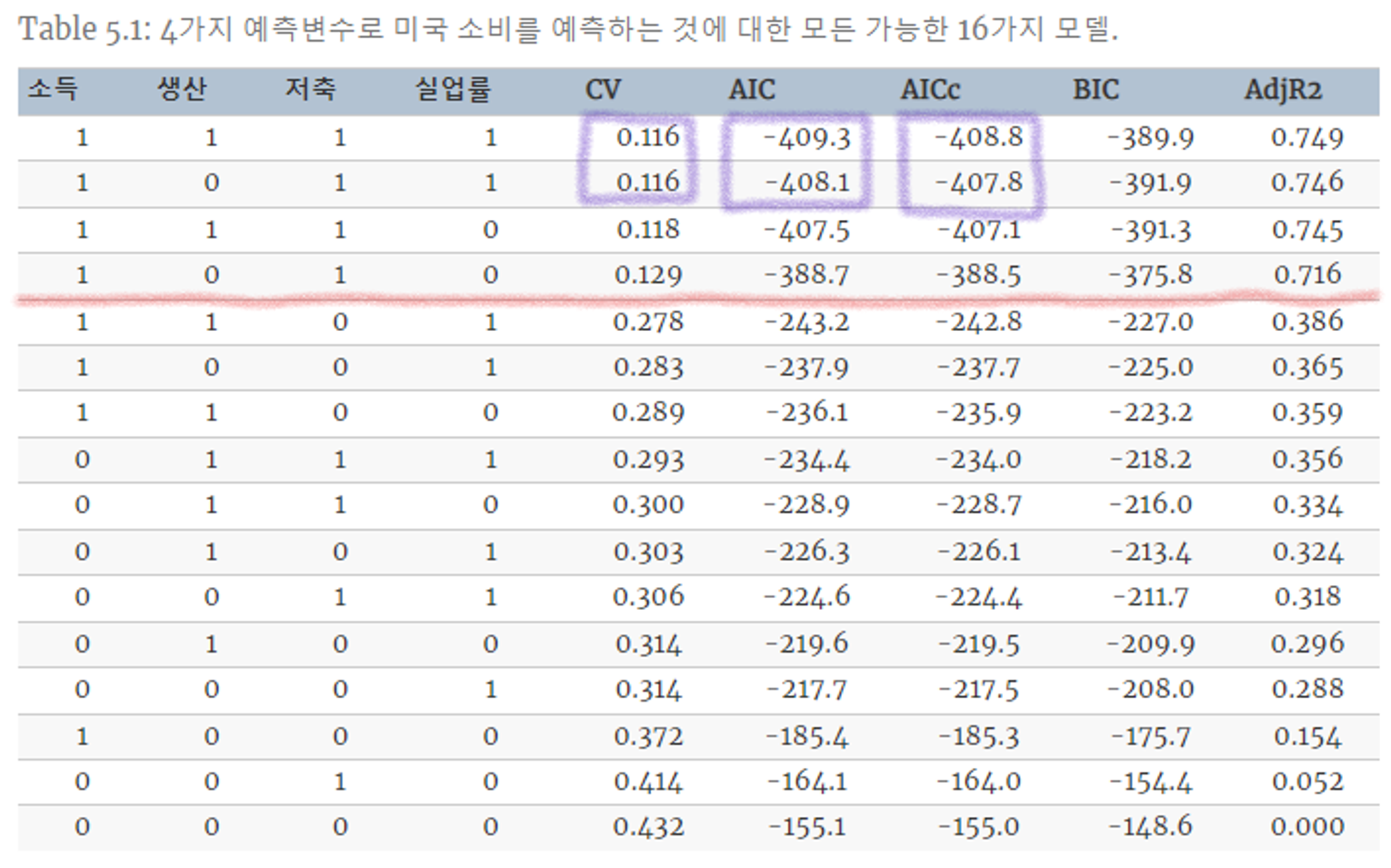
Table 5.1 : 4가지 예측변수에 대해, 사용(1), 제외(0) 으로 하여 16가지 경우의 수에 대해 실험을 진행한 결과이다. (AIC_c를 기준으로 오름차순 = 성능 순으로 내림차순)
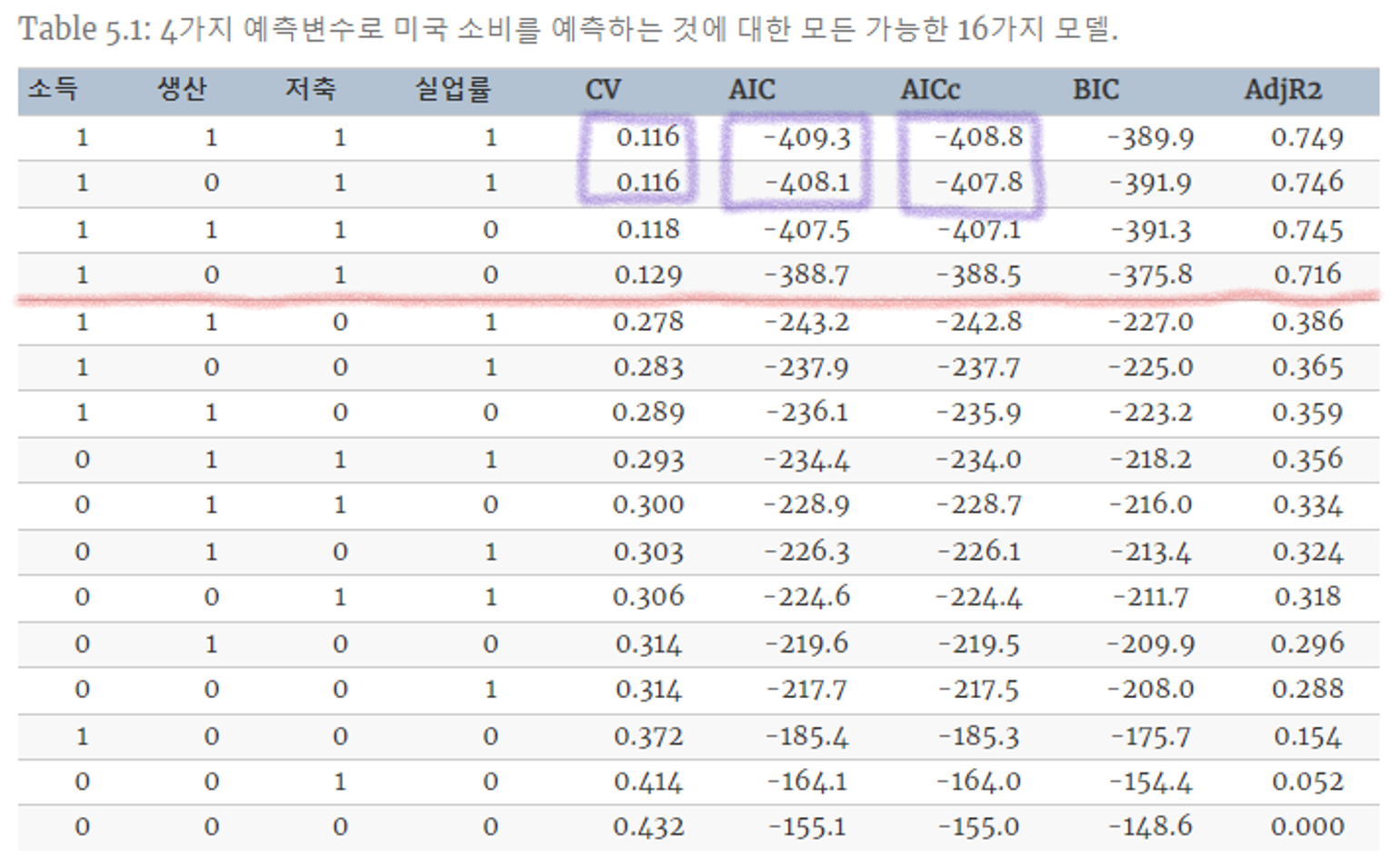
- 특징 1 : 상위 4개의 경우의 수와 나머지와의 큰 성능 차이가 존재한다. → 상위 4개의 경우 모두에 “소득”과 “저축”이 포함되어있다. → “소득”과 “저축”은 주요 예측변수 임을 알 수 있다.
- 특징 2 : 상위 2개의 경우 CV, AIC, AIC_c 가 거의 비슷하다. → 두 경우의 차이는 “생산” 예측변수에 대한 사용 차이 → “생산”은 성능에 큰 영향이 없는 변수로 무시(제외)해도 된다.
- 실제로 “생산”과 “실업률” 간 상관관계는 매우 높으며, 둘 중 하나의 변수만 사용해도 됨을 알 수 있다.
-
위와 같이, 가능한 경우의 수에 대해 모두 학습을 진행해보고,
여러 평가지표 중 하나에 근거하여 가장 좋은 모델을 고른다.
이렇게 선정된 모델을"가장 좋은 부분집합 회귀"(모든 가능한 부분집합) 라 한다.
5.5.8 단계적 회귀
- 현실적으로 수많은 경우의 수를 모두 학습시킬 수 없다. (예측변수가 40개라면 2^40개, 1조가 넘는 모델이다)
- 후진 단계적 회귀(backwards stepwise regression)
- 모든 예측변수를 사용하는 모델을 학습 후 평가한다.
- 예측변수 하나씩 제거해보면서, 예측 정확도가 높아지면 제거 후 반복한다.
- 후진 단계적 회귀(backwards stepwise regression)
- 예측변수가 너무 많으면 전진 단계적 회귀를 사용한다.
- 전진 단계적 회귀(forwards stepwise regression)
- 절편만 포함하는 모델을 학습 후 평가한다.
- 예측변수 하나씩 추가해보면서, 예측 정확도가 높아지면 추가 후 반복한다.
- 전진 단계적 회귀(forwards stepwise regression)
- 혼합절차도 존재한다.
- 예측변수의 일부를 포함하여 학습한 뒤, 제거와 추가를 모두 고려하여 반복한다.
- 어떤 방식이 가장 좋다는 것은 없지만, 대부분 좋은 모델을 찾을 수 있다.
