[Time Series] 회귀모델을 통한 예측

온라인 Forecasting 교재 [Forecasting : Principles and Practice] 5장 6절을 참고하여 작성하였습니다.

5.6 회귀로 예측하기

• y의 예측값 (미래 데이터에 대한 예측값이 필요하다.)
  $\hat y_t = \hat β_0+\hat β_1x_{1,t}+\hat β_2x_{2,t}+\hat β_3x_{3,t}+...+\hat β_kx_{k,t}$
• 위 식을 통해 y_hat을 산출하는데 이 때, 오차를 무시하고, 추정된 계수를 사용한다.
  • 하지만 이 때 구하는 값은 과거 데이터에 대한 적합값이다.

5.6.1 사전 예측 VS 사후 예측

• 사전 예측

  • 예측변수 x의 과거 데이터를 기반으로 예측한다.
  • 표본이 끝난 다음 분기의 사전 예측값은 이전까지의 데이터만 사용해야 한다.
  • 따라서 사전 예상값을 내려면 모델에 예측변수(predictor variable)의 미래 값(예상값)이 필요합니다.
    • 이를 위해 다양한 기법이 존재한다. (정부 기관에서 내놓은 예측값을 사용하는 것도 하나의 방법이 된다.

  ㄟ(▔,▔)ㄏ 따라서 사전 예상값을 내려면 모델에 예측변수(predictor variable)의 미래 값(예상값)이 필요합니다. ?
  
   사전 예측을 하는 “모델”은
   과거 데이터를 기반으로 미래 데이터를 예측해야 하기 때문에,
   미래 데이터를 활용한 학습이 필요하다. 
   (그래야 나중에 test에서도 미래 데이터를 예측할 것이니까)
  
   그래서 미래 값이 필요하다고 하는 것이다.

• 사후 예측

  • 예측변수 x의 미래 데이터를 기반으로 예측한다. (지나고 난 뒤 지난 일을 예측해본다.)

  • 관측한 실제 예측 변수 값을 사용하여 사후 예측값을 계산한다.
    이러한 예측값은 실제 예측값이 아니지만 예측 모델이 작동하는 것을 살펴볼 때 유용하다.

  • 사후 예측값은 예측변수 x에 대한 가정이 가능하지만,
    사후 예측값으로 목표 예상변수 y에 대한 가정을 해선 안된다.

    ㄟ(▔,▔)ㄏ
    관측한 실제 예측 변수 값을 사용하여 사후 예측값을 계산한다.
    이러한 예측값은 실제 예측값이 아니지만 예측 모델이 작동하는 것을 살펴볼 때 유용하다. ?
    
    사후 예측은
    이미 지난 시점을 모델의 예측 시점으로 잡고
    모델을 학습시켜 결과를 확인한다.
    
    이미 지난 시점이므로 해당 시점의 데이터가 존재하기 때문에,
    모델의 학습 성능을 파악할 수 있다.

• 사전 예측과 사후 예측값을 비교 평가하면 예측 불확실성의 원인을 파악할 수 있다.

  • 예측 모델의 성능 문제 (→ 사전 예측 관련) vs 예측변수에 대한 예측값 (→ 사후 예측 관련)

• 예제 : 호주 분기별 맥주 생산량

  

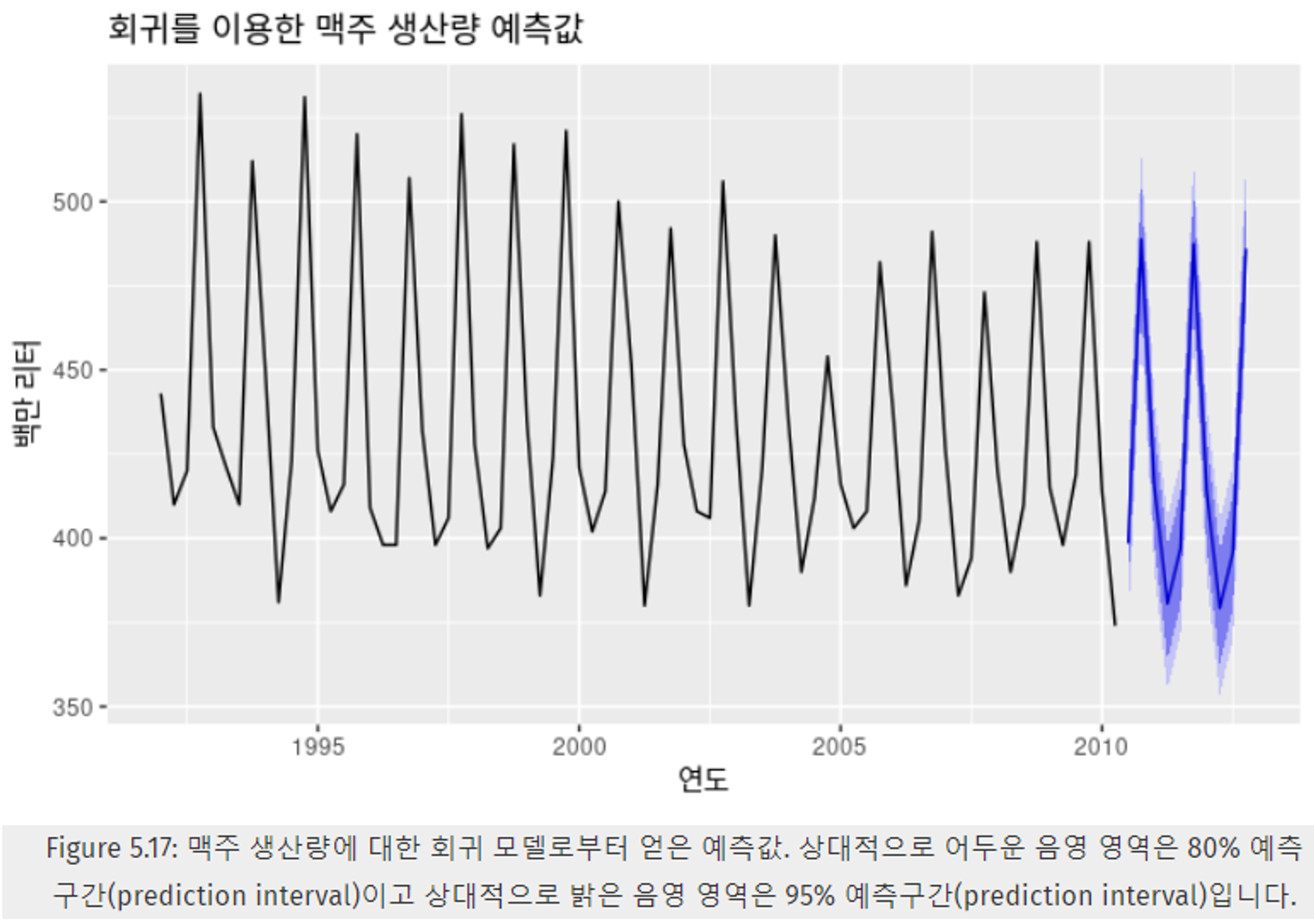
  • 일반적으로 사전 예측을 할 때, 미래 데이터를 알 수 없으므로 과거 데이터만을 사용한다.
  • 하지만, 예측변수의 달력 변수(계절성 가변수 등) 이나 시간의 확정적인 기능에 근거해 미리 파악할 수 있고, 이러한 경우 사전 예측과 사후 예측이 동일하다.

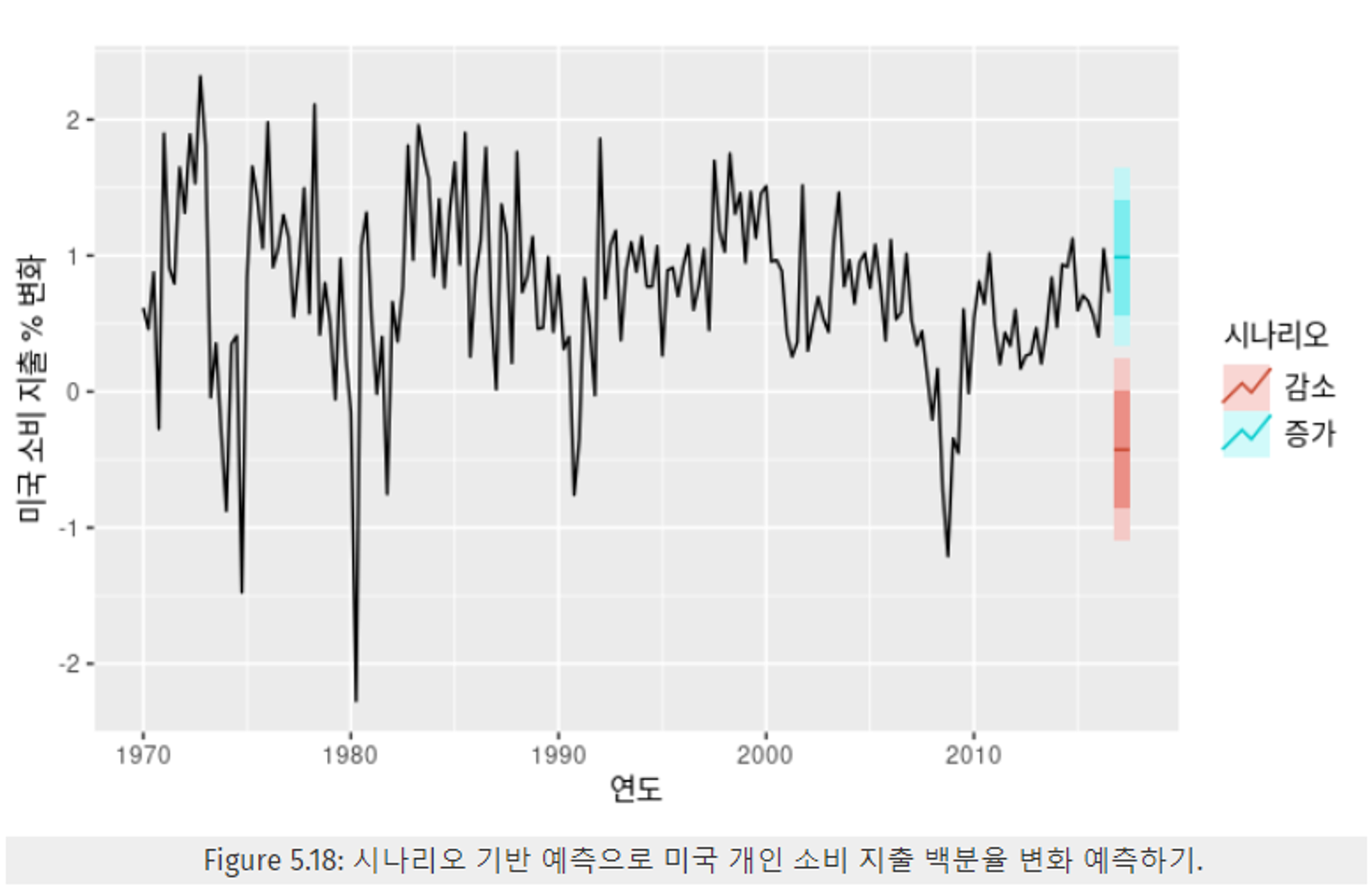
5.6.2 시나리오 기반 예측

• 관심 있는 예측변수에 대해 가능한 시나리오를 가정하여 예측하는 방법
• 예시 : 미국 정책 담당자가 고용률 변화 없이 득과 저축에 대해 각각 1.0% 0.5%의 지속적인 성정이 일어나는 것과, 각각 1%와 0.5%의 감소가 일어나는 상황을 시나리오로 구성한다. → 해당 시나리오에서 소비 측면의 예측된 변화량을 비교한다.
  
• 시나리오를 통해 예측변수의 미래 값을 미리 알고 있다고 가정하기 때문에 이에 따르는 불확실성을 포함하지 않는다.
  

5.6.3 예측 회귀 모델 세우기

• 회귀 모델의 가장 큰 장점
  • 관심있는 목표 예상변수 y와 예측변수 x의 중요한 관계를 구할 수 있다.
• 회귀 모델의 가장 큰 어려움
  • 사전 예측을 위해서, 각 예측변수의 미래값이 필요하다.
  • 사후 예측에서는 예측변수에 대한 예측값을 얻는 것이 어렵다.
    • “예측변수 x 없이 목적 예상변수만으로 목적 예상변수를 직접 예측하는 것”
      ”예측변수 x에 대한 예측값을 예측하는 것” 둘 중 후자가 더 어려울 수 있다.
• 대안 : 예측변수 x를 기반으로 한 시차 값을 사용한다.
  • h단계 이전의 예측에 관심이 있을 때, h=1, 2, … 에 대해 아래와 같은 식으로 표현할 수 있다.
    $y_{t,h}=β_0+β_1x_{1,t}+...+β_kx_{k,t}+ε_{t+h}$
  • 예측변수의 시차값을 포함하면 모델이 예측변수의 예측값을 더 쉽고 직관적으로 산출할 수 있다.
    • 예시 : 생산 증가를 목표로 하는 정책 변화의 효과는
      소비 지출에 바로 영향을 미치지 않고, 시차 효과가 함께 발생할 수 있다.
      → 예측변수인 소비 지출의 시차값을 포함함으로써 소비 지출의 예측값을 더 쉽게 산출 가능하다.
      

5.6.4 예측구간

• 주로 95%, 80%의 표현이 있다.
• 간단한 회귀에 대한 예측 구간 계산

  1. 한 예측값 y_hat에 대한 식

     $\hat y = \hat β_0 + \hat β_1x$

  2. 회귀 오차가 정규 분포를 따른다면, 위 예측값 y_hat 의 대략적인 95%의 예측구간은 아래와 같다.

     

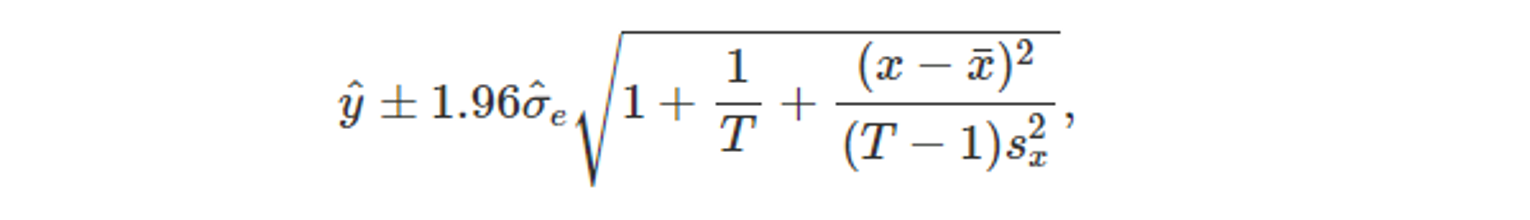
     • T : 관측값의 전체 개수
     • s_x : 관측된 x 값의 표준편차
     • σ_hat_e : 회귀모델의 표준 오차
     • 80% 예측 구간일 때 (1.96) → (1.28)
     • 관측된 x 값과 x_avg가 차이날 때, 예측구간이 넓어지고
       관측된 x 값이 평균과 가까울 때, 예측값을 더욱 확신하게 된다.

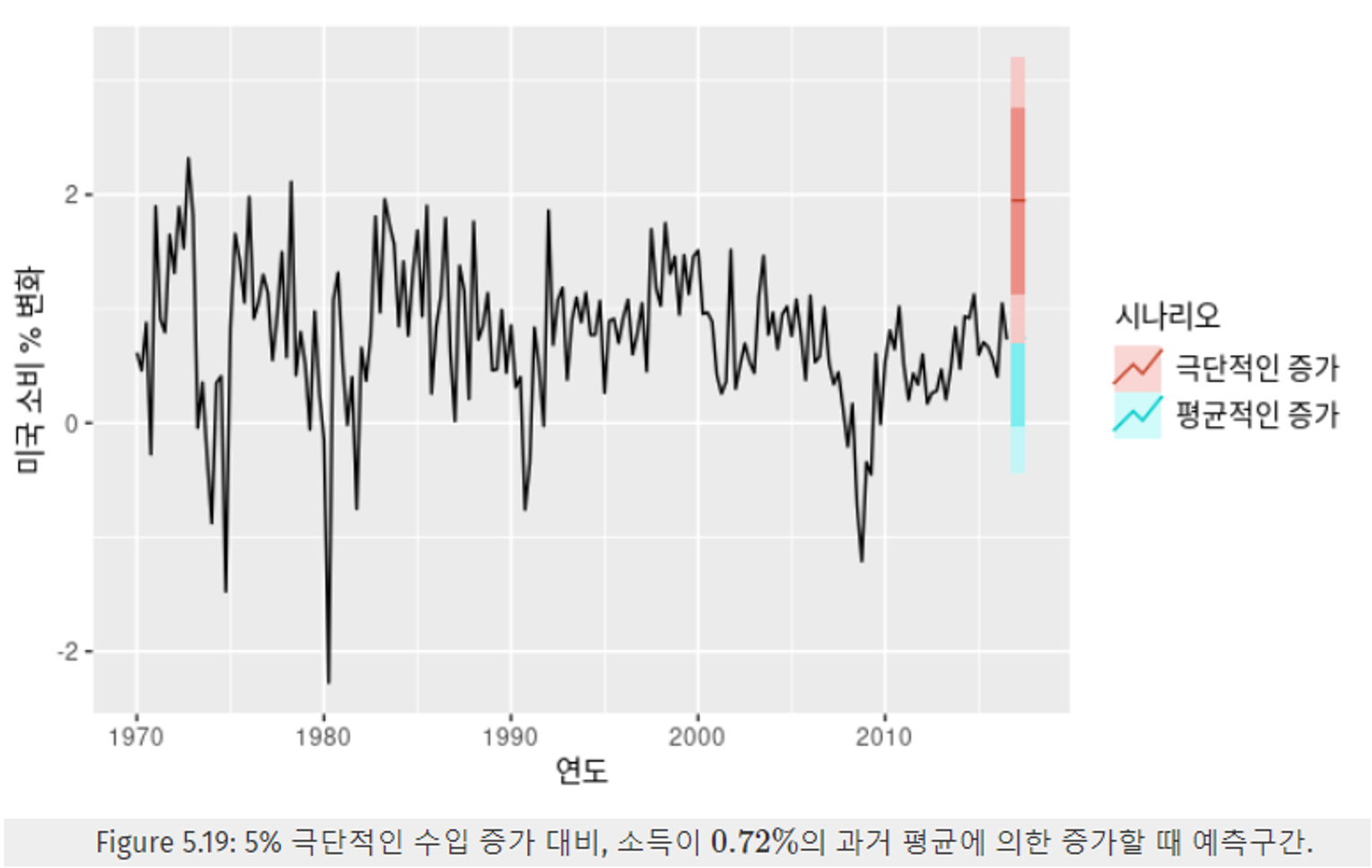
• 예제 : 미국 소비 예제
  $\hat y_t = 0.55 + 0.28x_t$
  • 4개 분기의 개인 소득 x의 평균 : 0.72%
  • 과거 평균 값만큼 증가할 것을 가정하면, 0.75%만큼 증가한다.
  • 95% 예측 구간은 [−0.45, 1.94] 80% 예측 구간은 [−0.03,1.52]
    
  • 5%의 극단적인 수입 증가가 발생한다? → 예측구간이 아래 Figure 5.19와 같이 극단적으로 증가한다.