[Time Series] 예측변수 예시

온라인 Forecasting 교재 [Forecasting : Principles and Practice] 5장 4절을 참고하여 작성하였습니다.

5.4 몇 가지 유용한 예측변수

• 시계열 데이터에 대해 회귀 분석을 진행할 때, 유용하고 자주 등장하는 예측 변수 7가지

5.4.1 추세

• 선형 추세는 단순히 예측 변수 x에 t를 추가하여 모델링할 수 있다.

• t = 1, … , T

5.4.2 가변수

• dummy variable, 모의 변수, 지표 변수(indicator variable)
• 범주형 변수 (Yes/No 등)을 1 또는 0의 모의 변수로 변환하는 것이다.
• 이상치에 대해 가변수 처리가 가능하다
  • 예시 : 브라질 여행자 데이터 → 2016 리우 올림픽 (1), 그 외 (0)으로 하여 이상치를 데이터에 반영하여 사용한다.
• 세 개 이상의 범주가 있을 때는, 변수를 범주의 개수만큼 가변수로 만들어서 부호화를 진행한다.

5.4.3 계절성 가변수

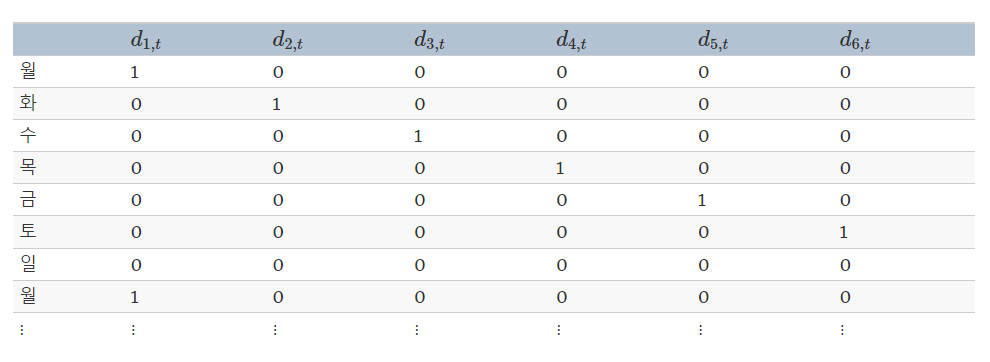
• 예시 : 일별 데이터 예측에 요일을 고려하고 싶을 때 → 6개의 가변수를 만들고, 월요일 1 0 0 0 0 0, 화요일 0 1 0 0 0 0 , …
  • 일반적인 규칙 : 범주보다 하나 적은 수의 가변수를 사용한다.
    • 가변수 함정(dummy variable trap)
      • 7개의 범주에 7개의 가변수를 쓰면 회귀가 실패할 것이다.
    • y 절편까지 고려한다면, (계절성 가변수)를 사용하는 것은 좋지만, 최소한의 예측 변수 추가를 진행한다.
  • 가변수와 관계된 각 계수는 생략된 범주에 관한 해당 범주의 효과를 나타냅니다.
    • 월요일과 관계된 d1,t의 계수는 y에 대해
      일요일의 효과와 비교하여 월요일의 효과를 나타냅니다.

ㄟ(▔,▔)ㄏ 
가변수와 관계된 각 계수는 
생략된 범주에 관한 해당 범주의 효과를 나타냅니다 ?

아래 예시를 통해 파악한 내용으로

가변수 = 각 요일에 대해 생성된 가변수
관계된 각 계수 = 각 가변수에 곱해지는 계수 β
생략된 범주 = 해당 가변수가 아닌 다른 가변수 
            (월요일일 때 1인 가변수 1개와 0인 가변수 5개라 할 때, 5개의 가변수)
해당 범주 = 해당 가변수 
           (월요일일 때 1인 가변수 1개와 0인 가변수 5개라 할 때, 1개의 가변수)

가변수와 관계된 각 계수는 생략된 범주에 관한 해당 범주의 효과 
= “해당 가변수의 계수는 다른 가변수들에 관한 해당 가변수의 효과”

5.4.4 개입 변수

• 예측하려는 변수에 영향을 줄 수도 있는 값을 모델링에 반영하기 위해 사용하는 변수
• 예시 : 경쟁자의 활동, 광고 지출, 산업 행동 등
• 스파이크(spike) 변수
  • 효과가 한 주기만 지속될 때 사용한다.
  • 효과가 지속되는 주기(개입 기간)에는 1, 그 외에는 0으로 두는 가변수 형태이다.
• 즉각적이고 영구적인 효과가 있다.
  • 그래프 상에서는 기울기의 변화로 나타난다. 기울기의 변화로 인해 개입 시점에서 추세가 구부러지므로 추세가 비선형적으로 바뀌게 된다.
• 단계(step) 변수
  • 개입 변수는 즉각적이고 영구적인 효과가 있기 때문에,
  • 이러한 개입이 수준 변화를 일으킬 때 (=시계열의 값이 개입 시점부터 영구적으로 변할 때)
    개입 전을 0, 개입 후를 1로 두는 가변수 형태로 사용한다.

5.4.5 거래일 수

• 판매량 데이터에서 각 월의 거래일 수를 예측 변수로 포함한다.
  • Why? 판매량 데이터에서 매월 거래일의 날짜 수가 많이 변할 수 있는데, 날짜 수가 많을수록 주로 판매량이 커지기 때문에 이를 예측 변수로 포함하여 설명력을 높인다.
• 주마다 날짜 수가 다른 효과를 고려하기 위해 해당 월의 월요일 수, 화요일 수, … 까지 예측 변수로 추가한다.

5.4.6 분포된 시차 값(lagged value)

• 광고 효과 데이터에서 광고 지출을 예측 변수로 넣는 경우가 종종 있는데,
  광고 효과가 실제 계획한 캠페인 기간(즉, 광고 비용을 지출하는 기간)보다 더 오래갈 수 있기 때문에
• 광고 비용 지출에 대한 시차값(lagged value)을 예측 변수로 추가함으로써 지출에 비해 몇 개월이나 더 지속되었는지 파악할 수 있게 한다.

5.4.7 부활절

• 부활절은 매년 날짜가 다르고, 효과가 며칠동안 지속될 수 있다. ⇒ 대부분의 휴일과 다르다.
• 부활절의 영향을 주는 기간을 1, 그 외의 기간을 0으로 하는 가변수 형태로 예측변수에 추가할 수 있다. (3월이면 3월에 1, 3월~4월이면 가변수를 월 사이에 비례하여 나눈다.)

5.4.8 푸리에 급수

• 사인과 코사인 항의 급수로 임의의 주기적 함수의 근사치를 계산하는 방식
  → 계절성 패턴을 다룰 때 사용할 수 있다.
• 계절성 가변수가 아닌, 긴 계절성 주기에 대해서 푸리에 항을 사용한다.
  
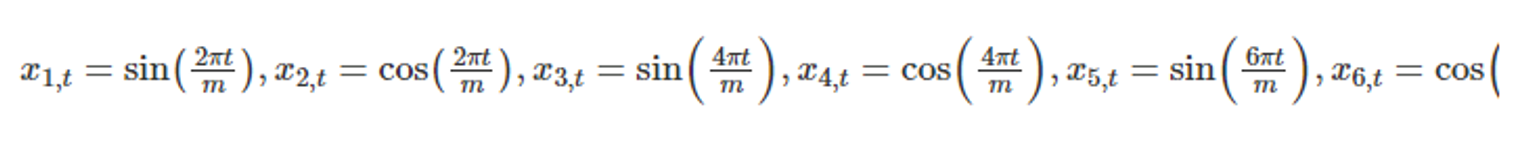
  • m : 계절성 주기 (월별 데이터 m=12, 분기별 데이터 m=4)

• 예시 : 월별 계절성을 다룬다고 하자. 가변수를 사용할 때, 12개의 범주(m=12) → 11개의 가변수 푸리에 급수를 사용할 때, K = m/2 → 6개의 푸리에 항으로 표현 가능
  
• 계절성 주기가 클수록 푸리에 급수의 효과가 증가한다. (주별 데이터 m=52)