[Time Series] 회귀 모델 평가

c_10.log·2023년 12월 15일

Time Series forecasting

Time Series 📈

목록 보기

6/24

온라인 Forecasting 교재 [Forecasting : Principles and Practice] 5장 3절을 참고하여 작성하였습니다.

5.3 회귀 모델 평가

잔차
- 학습-모음 오차
- 관측된 y 값과 해당하는 적합값 y_hat 사이의 차이 값
  $e_t = y_t - \hat y_t$ $= y_t - \hat β_0 - \hat β_1x_{1,t}-...-\hat β_kx_{k,t}$
- 각 잔차(residual)는 각 적합값 y_hat에 오차(예측할 수 없는 성분)
- 유용한 성질 2가지
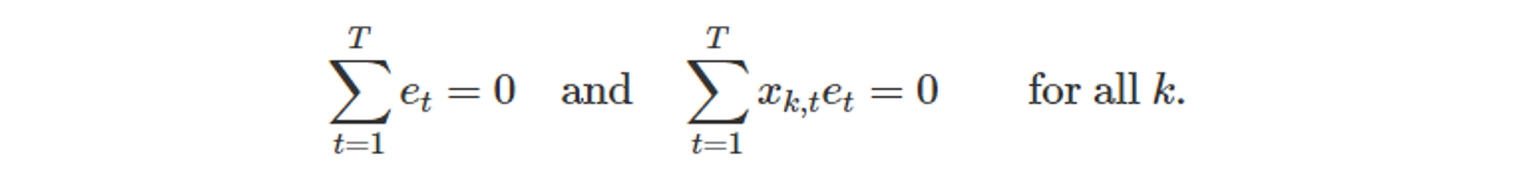
  1. 잔차의 평균은 0이다.
  2. 잔차와 예측변수에 대한 관측값 사이의 상관관계는 0이다.
- 회귀 변수 및 모델을 구축한 뒤, 모델의 가정이 만족되는지 확인하기 위해 잔차를 그려봐야한다.
  - 보다 자세하게는, 적합 모델(fitted model)과 기본 가정의 서로 다른 측면을 확인하기 위해 그래야할 그래프가 존재한다.

5.3.1 잔차의 ACF(자기상관함수) 그래프

잔차의 ACF 그래프를 그려봐야하는 이유?
1. 시계열 데이터는 현재 시점의 관측 값이 이전 기간의 값과 비슷할 것이기 때문에 잔차에 대한 자기상관관계를 파악한다.
  - 그렇게 되면, ”오차는 자기상관이 없다”는 가정이 위배되어 예측 성능이 떨어질 수 있다. (5. 시계열 회귀 모델의 “가정” 내용 참고)
  - “자기상관이 존재하는 오차”를 가진다 해도, 값이 편향되어있지 않다면, 모델이 잘못된 것은 아니지만,
    - 보통보다 더 큰 예측 구간을 가지게 된다.
      - 이를 해결하기 위해 항상 잔차의 ACF 그래프를 확인해야 한다.
브로이쉬-갓프레이(Breusch-Godfrey) 검정
- 계열 상관 (serial correlation)에 대한 LM(Lagrange Multiplier) 검정
- 회귀 모델을 고려하여 설계한 잔차의 자기상관을 확인하는 방법이다.
- 어떤 특정한 순서까지 잔차에 자기상관이 없다는
  결합 가설을 검증하기 위해 사용한다.
  - 방법
  p-value가 작을 때,
  잔차에 중요한 자기상관이 남아있다는 것을 나타낸다.
- 융-박스(Ljung-Box) 검정과 비슷하지만, 회귀 모델을 위해 설계된 검정이라는 것이 다르다.

5.3.2 잔차의 히스토그램

잔차가 정규 분포를 따르는지 확인하기 위해 히스토그램을 확인한다.
- 정규 분포를 따르는지 확인하는 것은 필수적이진 않지만, 예측 구간을 계산할 때 쉽게 계산할 수 있다.
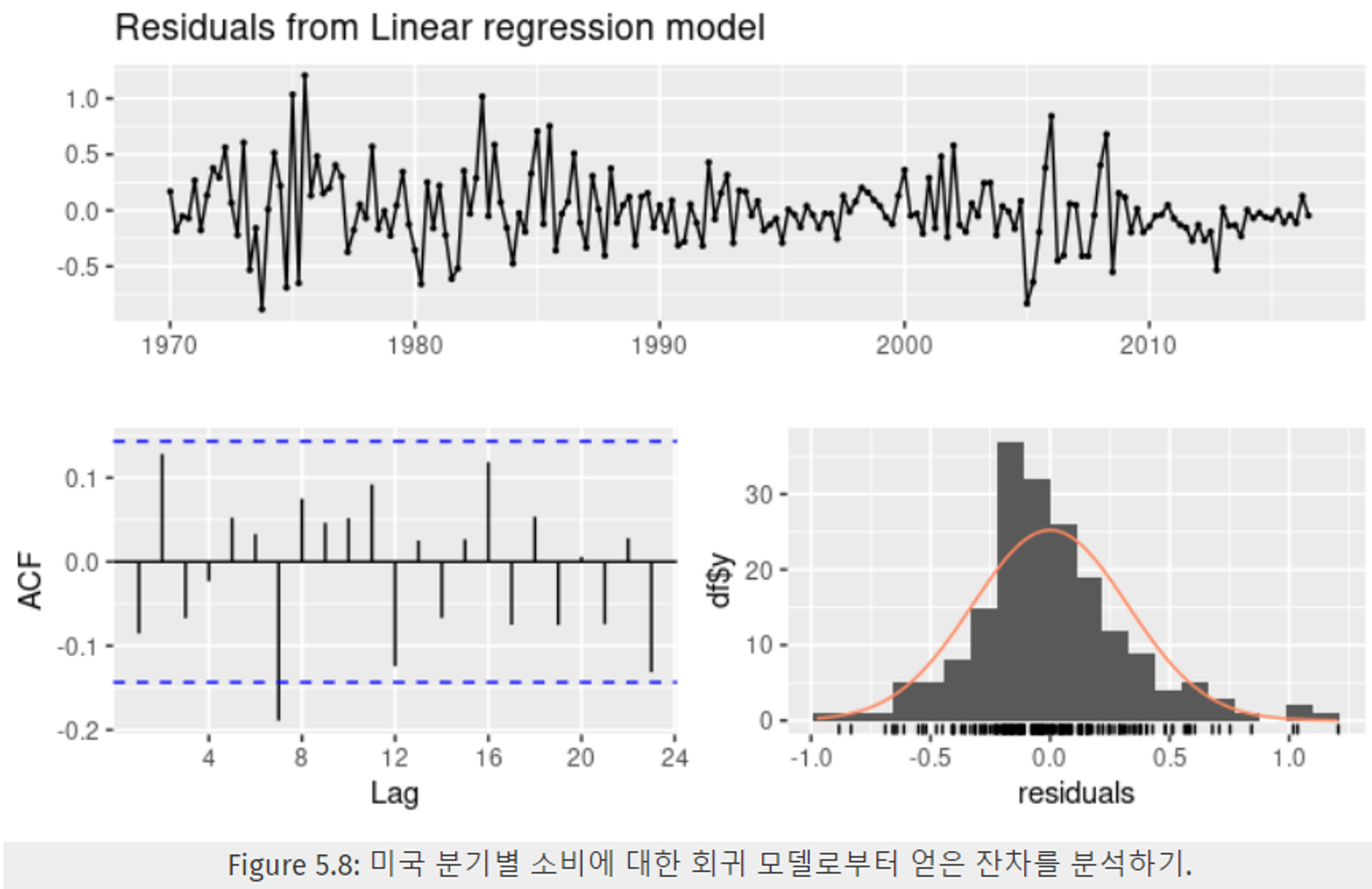
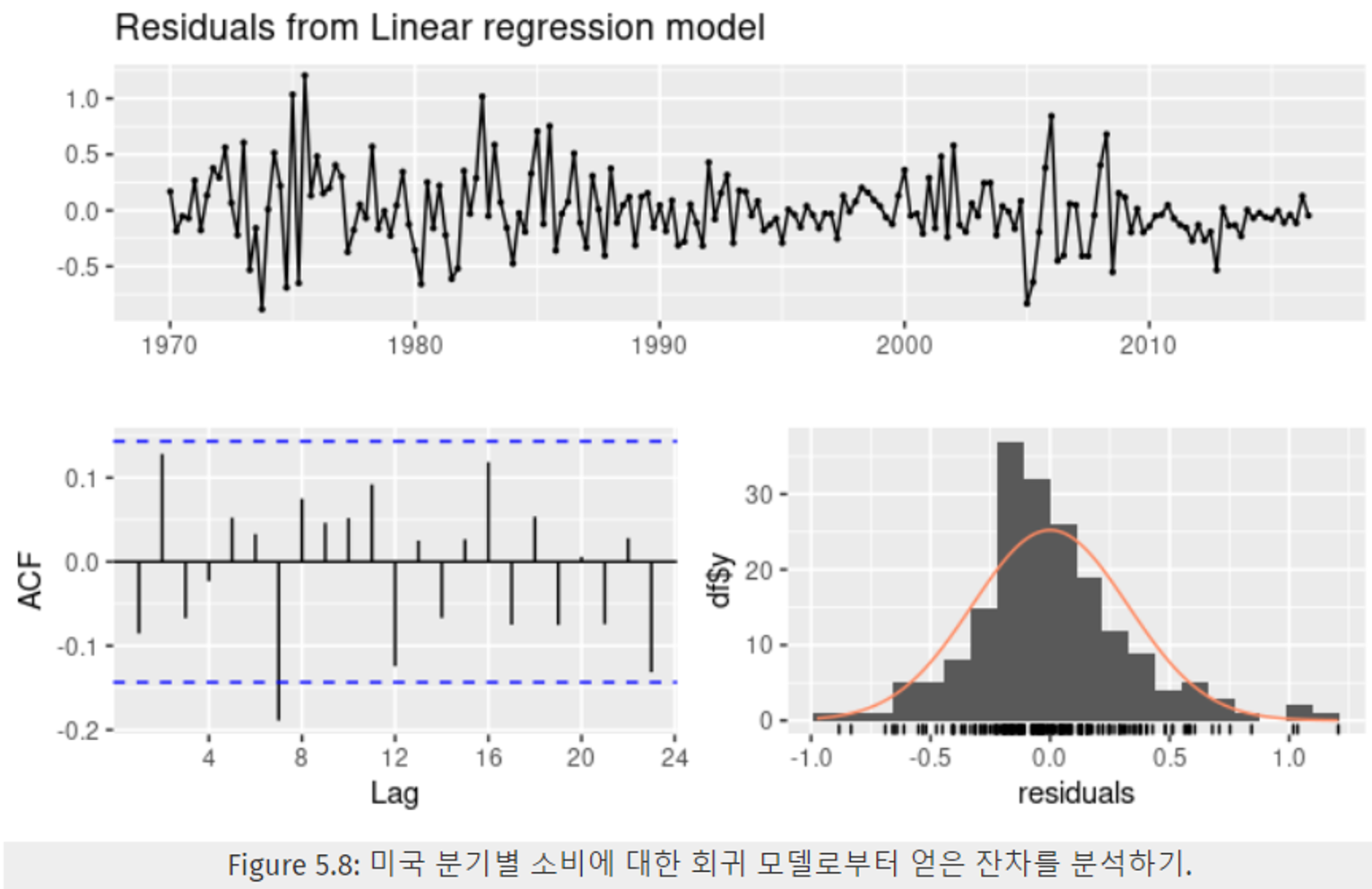
- Figure 5.8은
  미국 분기별 소비 잔차 time plot(위),
  자기상관함수 ACF(좌하단),
  다중 회귀 모델로 얻은 잔차의 히스토그램 (우하단)을 나타낸다.
- time plot 은 몇몇 부분에서 시간에 따라 변하긴 하지만, 나머지가 상대적으로 두드러지진 않는다. → 이를 이분산성(heteroskedasticity)이라 하고, 예측 구간 범위를 정확히 구할 수 없게 된다.
```
ㄟ(▔,▔)ㄏ
시계열 데이터는 값의 변동이 크게 없다면, 분석에 적절한 데이터가 아니다.
```
- 우하단의 잔차에 대한 히스토그램을 보면, 우측으로 살짝 기울어짐을 알 수 있다 → 예측 구간의 범위 확률에 영향을 줄 수 있다.
- 좌하단의 자기상관 그래프를 보면 t=7에서 큰 음의 값을 보임을 알 수 있다. (파란 점선 ±2/√T 을 넘는다.) 하지만 유의미하지 않음을 확인함.(브로이쉬-갓프레이(Breusch-Godfrey) 검정에서 5% 수준에 도달하였다.)
  ⇒ 자기상관 값이 크지 않다 + 시차 7에서의 자기상관 값이 크긴 하지만, 브로이쉬-갓프레이 검정을 통해 이 값도 예측값이나 예측구간에 영향을 줄 것 같지 않다.
```
#>  Breusch-Godfrey test for serial correlation of order
#>  up to 8
#>
#>  data:  Residuals from Linear regression model
#>  LM test = 15, df = 8, p-value = 0.06
```
- 위 코드는 8차까지의 자기 상관을 확인하기 위한 브로이쉬-갓프레이(Breusch-Godfrey) 검정 결과이다.

5.3.3 예측변수 x에 대한 잔차 그래프

각 예측변수에 대한 잔차의 산점도를 살펴본다.
- 잔차가 체계적인 패턴을 보이지 않고 무작위로 흩뿌려진 형태인지 확인할 수 있다. → 모델에 사용하기 적합한 예측변수이다.
산점도에서 패턴이 나타난다면, 데이터가 비선형 관계임을 알 수 있다.
"모델에 없는 모든 예측변수(predictor variable)에 대해 잔차(residual)를 그리는 것도 필요합니다."
모델 구축 전, 모든 예측변수에 대한 잔차를 그림으로서 패턴을 파악하고,
해당 예측변수가 비선형관계를 가짐을 파악한 뒤,
관련된 예측변수를 모델에 넣어야 한다.

ㄟ(▔,▔)ㄏ
"모델에 없는 모든 예측변수(predictor variable)에 대해 
잔차(residual)를 그리는 것도 필요합니다."?

잔차(residual)는 실제값과 모델이 예측한 값과의 차이로 알고 있는데,
모델이 없는 예측변수에 대해 잔차를 어떻게 확인할 수 있는지 모르겠다.

5.3.3 예제 : 미국 소비 지출

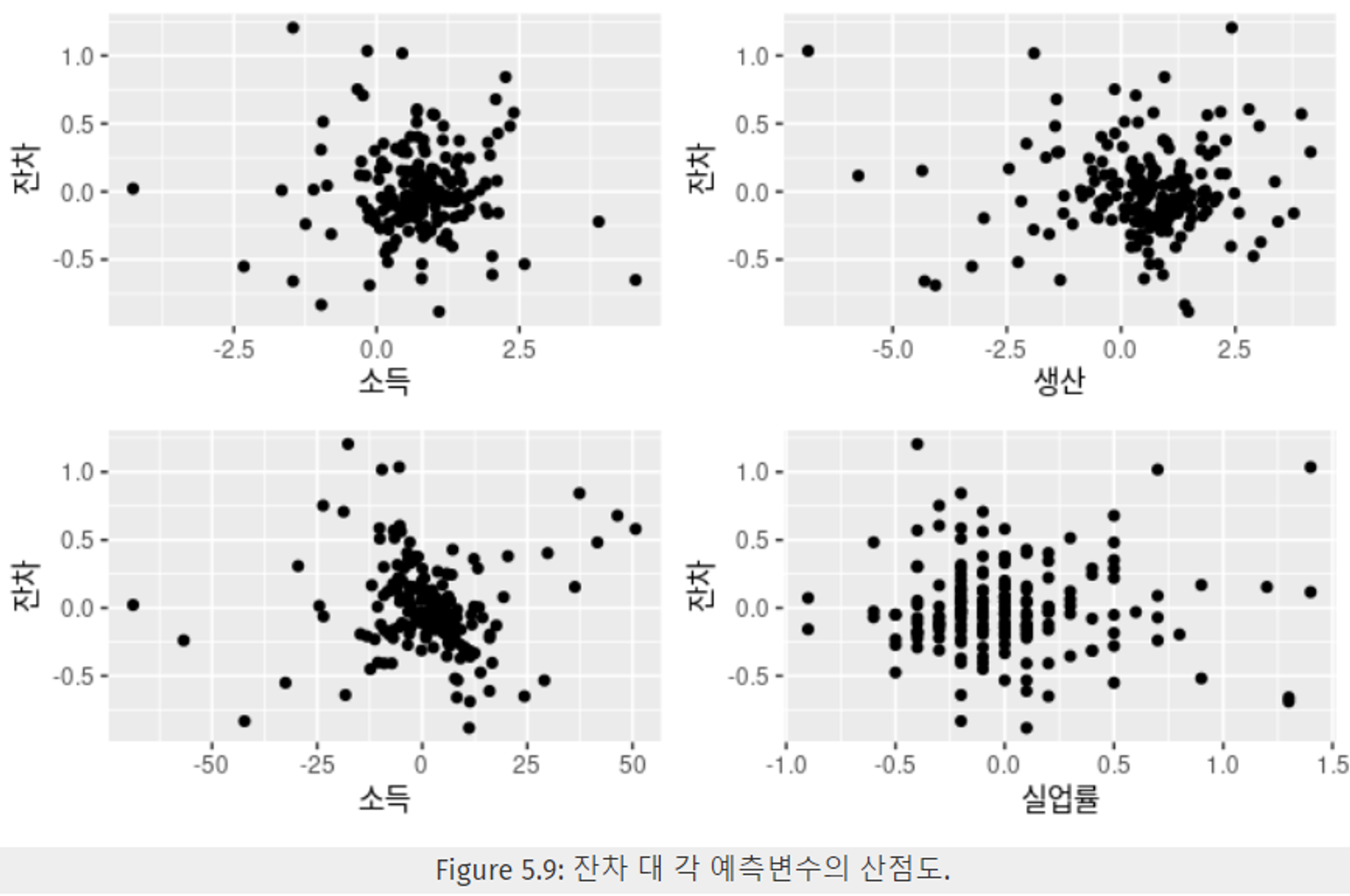
다중 회귀 모델에서 얻은 잔차를 각 예측변수 x에 대해 나타낸 결과이다. 4개의 예측변수 모두 산점도에서 흩뿌려진 결과를 보인다.

5.3.4 적합값에 대한 잔차 그래프

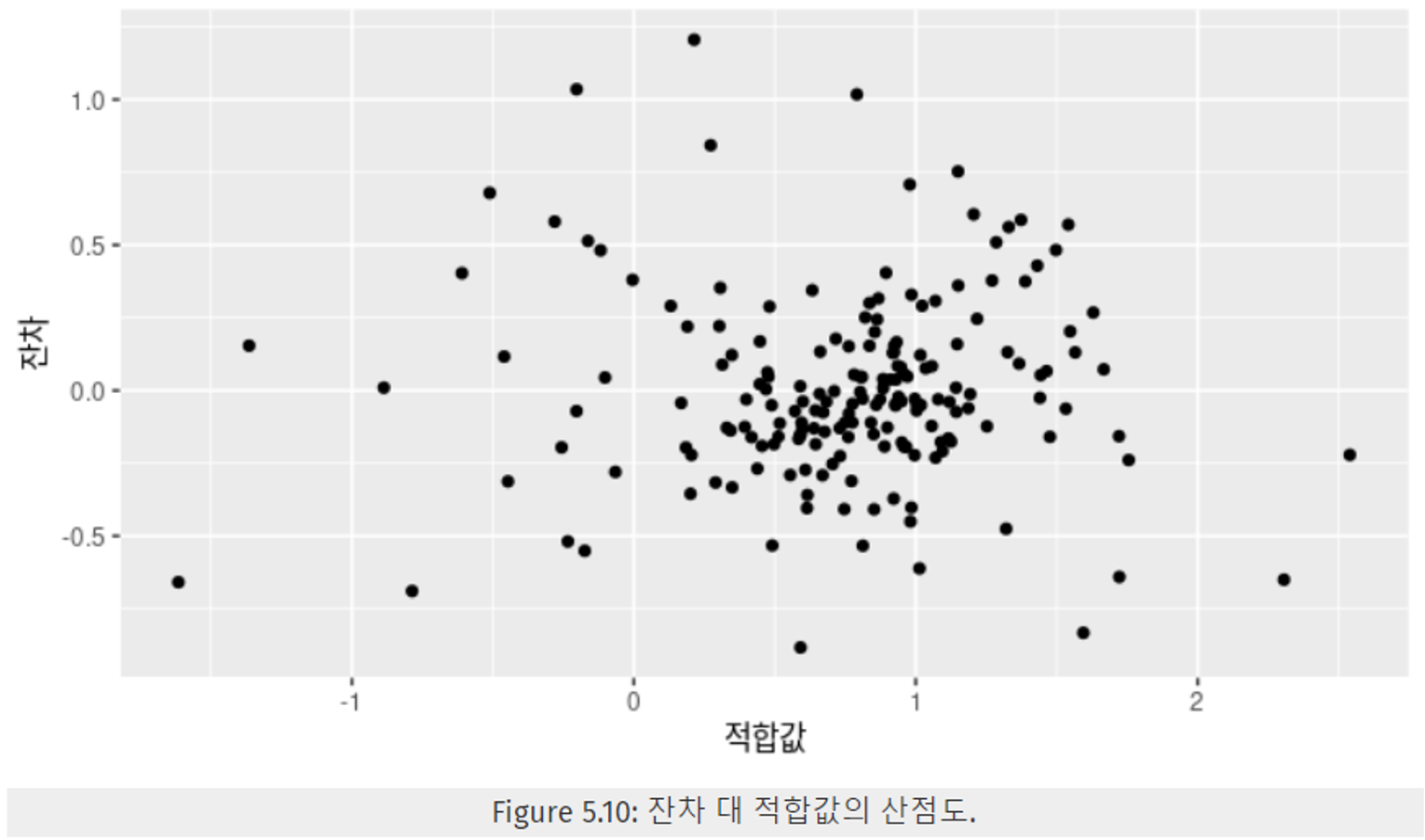
적합값에 대한 잔차의 산점도를 살펴본다.
- 어떠한 패턴도 나타나지 않아야 한다. → 오차에 등분산성 존재
- 패턴이 존재한다면, 오차에 이분산성 존재(값이 몇몇 곳에서만 변화하고 나머지는 유지 ⇒ 확률분포가 일정하지 않음) → 잔차의 분산이 일정하지 않다.
  - 이러한 문제가 생기면 목표 예상변수에 로그나 제곱근과 같은 변환이 필요하다.

5.3.5 이상값과 영향력 있는 관측값

이상값 (outliers) : 대다수의 데이터에 비해 극단적인 값을 갖는 관측값
영향력 있는 관측값 : 회귀 모형의 추정된 계수 β에 큰 영향을 주는 관측값
- 보통, x 방향에서 극단적인 값을 갖는 이상값이 영향력 있는 관측값이기도 하다.
x에 대해 y를 산점도로 나타내는 것은 회귀 분석을 시작할 때, 항상 도움이 되는 방식이고, 이 때 outliers를 찾아낼 수 있다.
이상값(outliers)의 근거
- 잘못 입력되었다? → 제거
- 관측값이 단순히 다르다? → 영향력 있는 관측값에 해당할 수 있다. → 무작정 제거 X → 조사를 통해 제거/유지에 대한 근거를 찾아야 한다.
예시
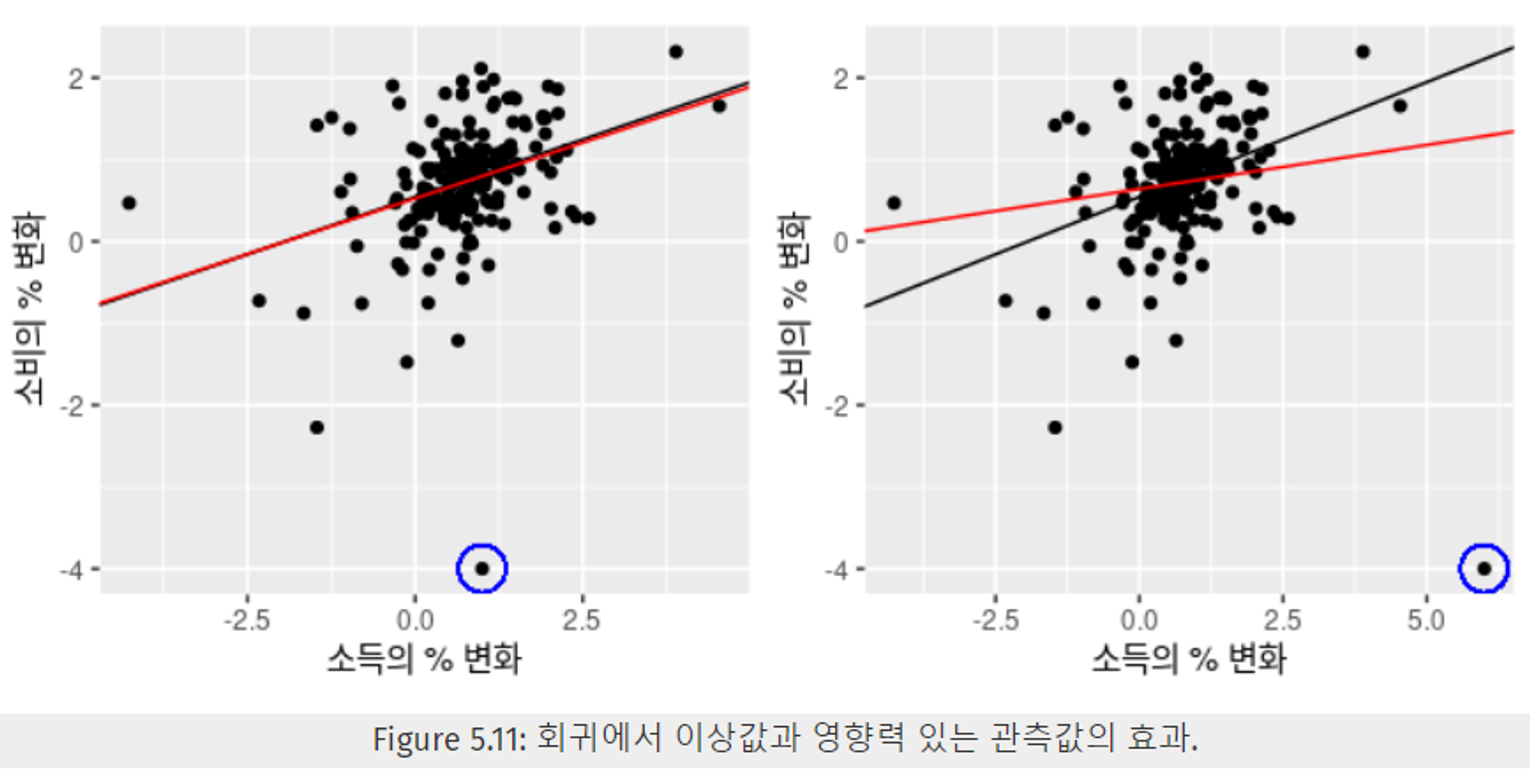
- Figure 5.11의 왼쪽 그래프의 이상치
  - y 방향으로 극단적인 값을 가진다. & 해당 값을 제거하고 선형 회귀식을 작성해도 큰 변화가 없다.
  - 이상치이지만, 영향력 X
- Figure 5.11의 오른쪽 그래프 이상치
  - x, y 두 방향으로 극단적인 값을 가진다. & 해당 값을 제거하고 선형 회귀식을 작성할 때, 큰 변화가 존재한다.
  - 이상치이면서, 영향력 있는 관측값이다.

5.3.6 허위 회귀

대부분의 시계열 데이터에서는 “정상성(stationarity)이 없다.” = 시계열의 값이 일정한 평균이나 일정한 분산으로 변하지 않고, 들쑥날쑥하다.
정상성이 없는 데이터를 회귀 분석 하는 것은 허위회귀로 이어질 수 있다.
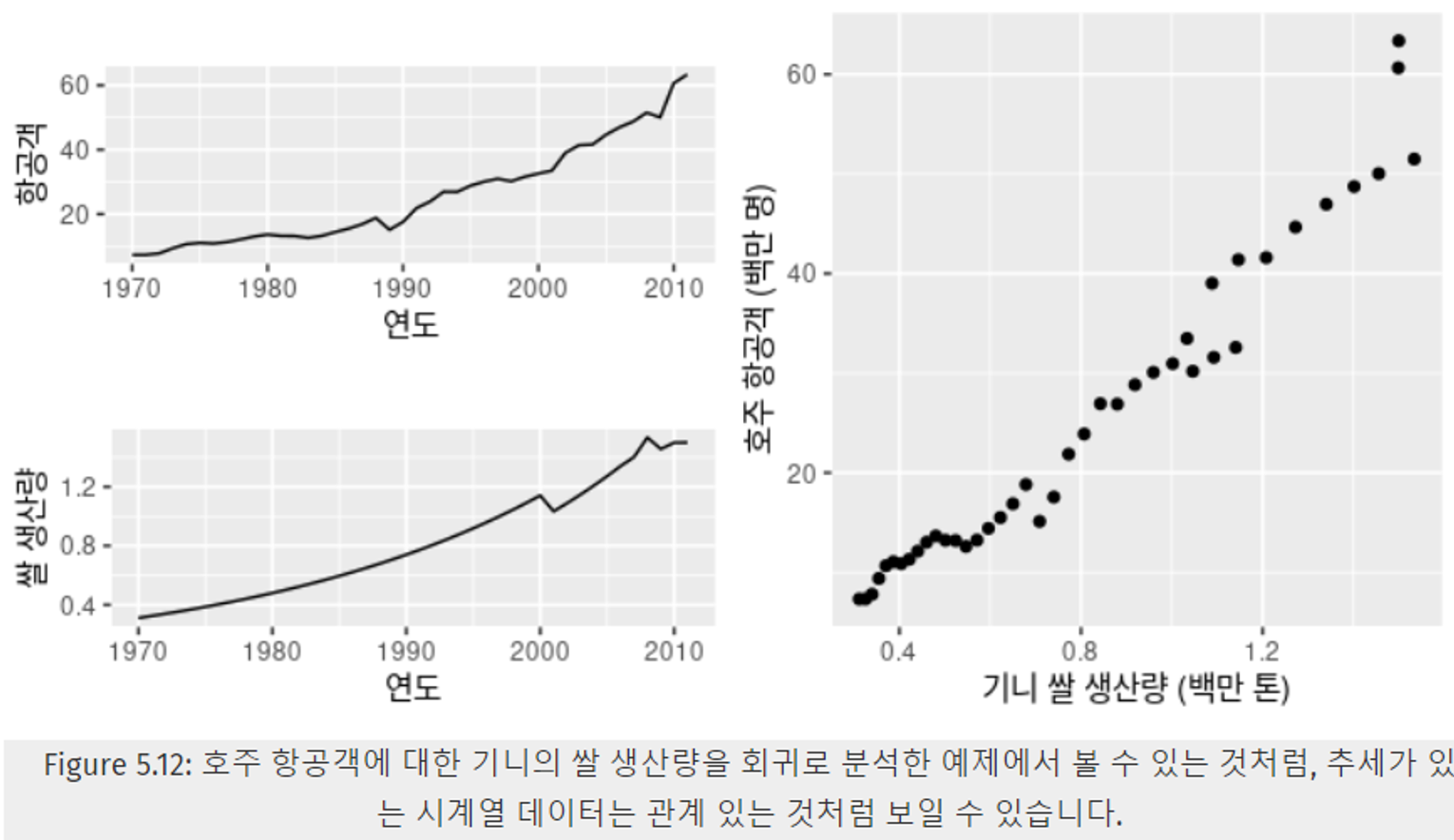
- Figure 5.12에서 보 두 데이터는 둘다 상향 추세를 보이고, 강한 양의 상관관계를 보이며 관계가 있다고 볼 수 있지만, 실제로는 전혀 관련 없는 데이터이다.
  - 이러한 데이터를 보고 어떻게 관계가 없다고 증명하는가?
    1. R^2 score 가 높다.
    2. 잔차(residual)에 대한 자기 상관 값이 높다.
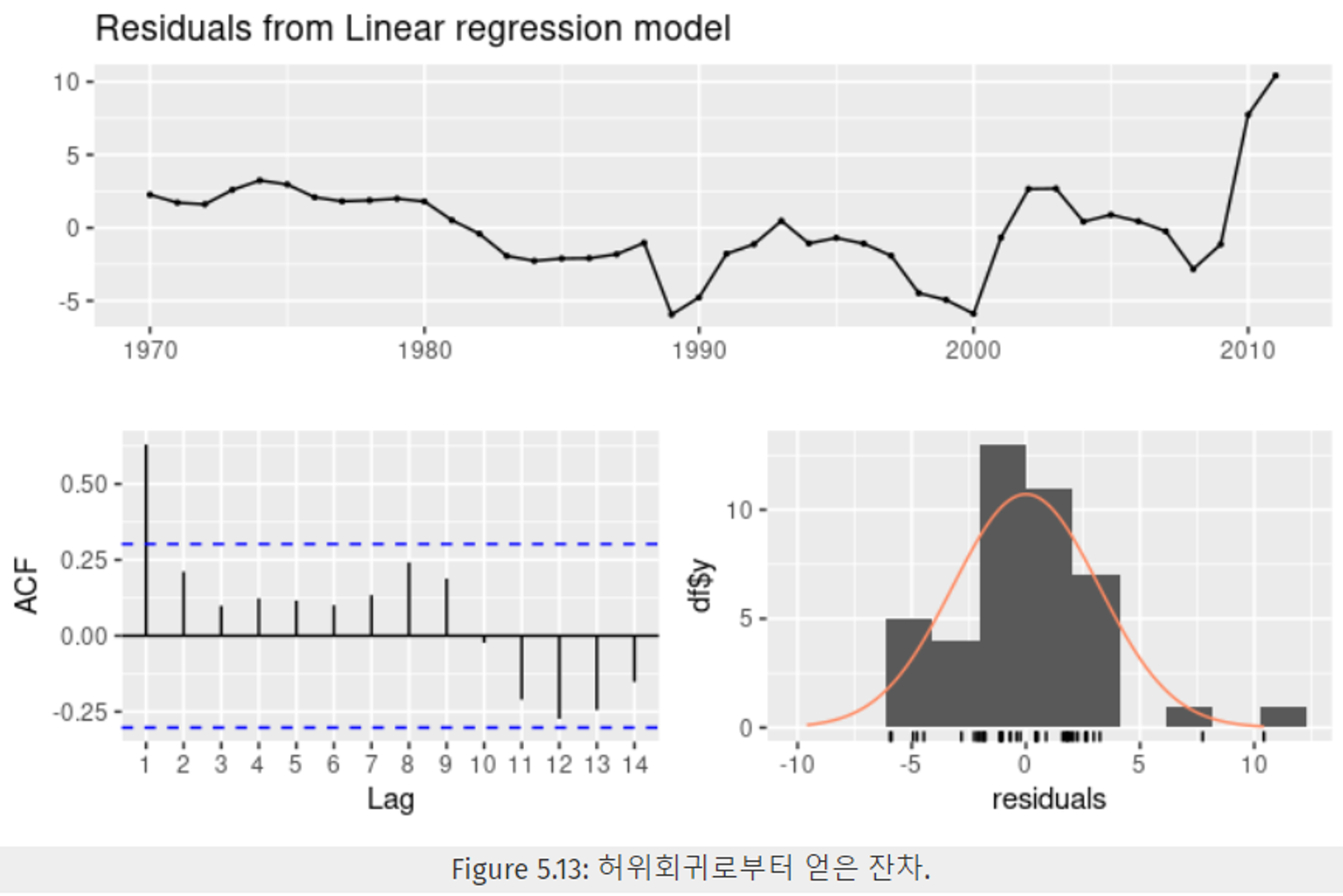
    - k=1에서 잔차에 대한 자기 상관 값이 매우 크다 → 허위 회귀
    - R^2 score 0.958 → 매우 큰 R^2 score → 허위 회귀