온라인 Forecasting 교재 [Forecasting : Principles and Practice] 7장 1절을 참고하여 작성하였습니다.

7. 지수평활

• “가장 최근 관측값이 가장 높은 가중치를 갖는다”

7.1 단순 지수 평활

• simple exponential smoothing, 단일 지수 평활(single exponential smoothing)
• 추세나 계절성 패턴이 없는 데이터를 예측할 때 사용하는 방법이다.
• 오래된 관측값보다 더 최근 관측값에 더 큰 가중치를 주는 방법
• 단순 기법 사용 시,
  
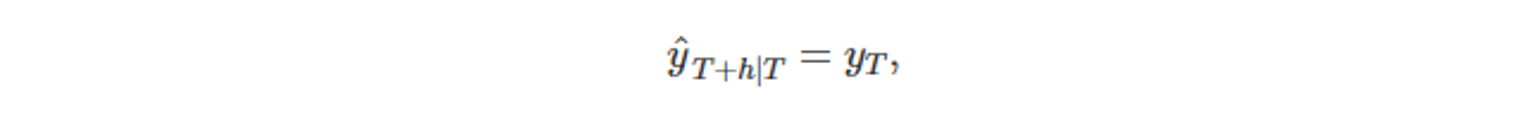
  • 모든 미래 예측값 = 시계열의 마지막 관측값
    • Why? 가장 최근 관측값만 가장 중요한 유일한 값
      & 이전의 모든 관측값의 정보는 미래 예측에 도움 X

• 평균 기법 사용 시,
  
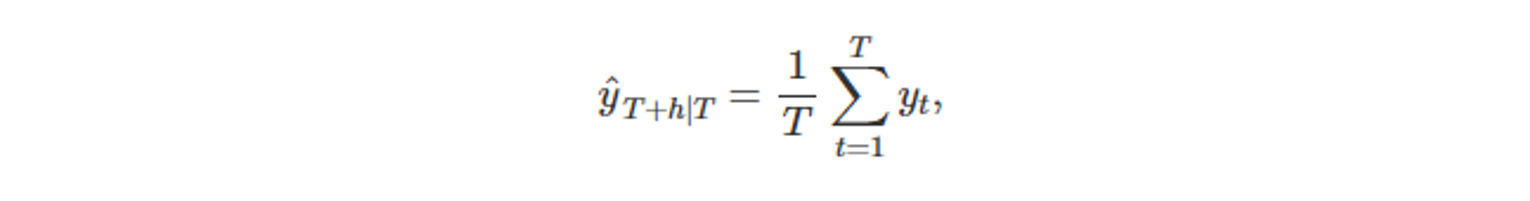
  • 모든 관측값이 동일하게 중요하다.
  • 모든 미래 예측값 ⇒ 모든 같은 가중치 부여

• 단순 지수 평활 사용 시,
  
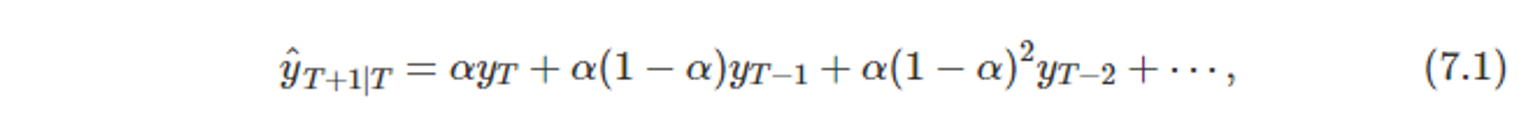
  • yhat(T+1|T) : one-step-ahead forecast(T+1에 대한 한 단계 앞 예측치)
    • y_1, … , y_T 의 모든 관측값을 가중 평균하여 얻은 값이다.
  • α : 평활 매개변수 (0≤α≤1)
    • 가중치 감소 비율을 조정한다.
    • α가 작을 때, 더 먼 과거 관측값의 가중치가 커진다.
    • α가 클 때, 더 최근 과거 관측값의 가중치가 커진다. (1인 경우, 단순 예측 기법과 동일)
    • 어떤 α 이더라도, 관측치에 붙는 가중치는 과거로 갈수록 감소한다.
    • 어떤 α 이더라도, 가중치의 합은 근사적으로 1이다.

7.1.1 가중 평균 형태

• 단순 지수 평활 식 7.1 에 대한 다른 표현 형태

  • 시간 T+1 의 예측 = 시간 T의 예측 + 가장 최근 관측값
    

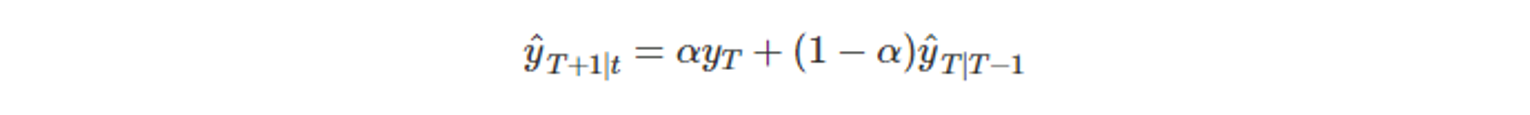
  • t = 1, … , T 일 때, 적합값을 보면 아래와 같을 것이다.
    

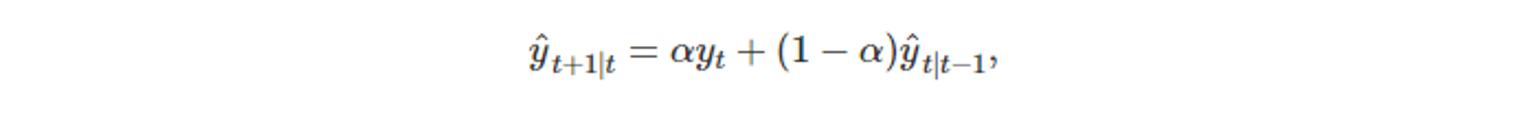
    • 이 단계는 one-step-forecast 이기 때문에, t=1 일 때 적합값을 ℓ_0라 가정하면 아래의 식이 성립한다.
      
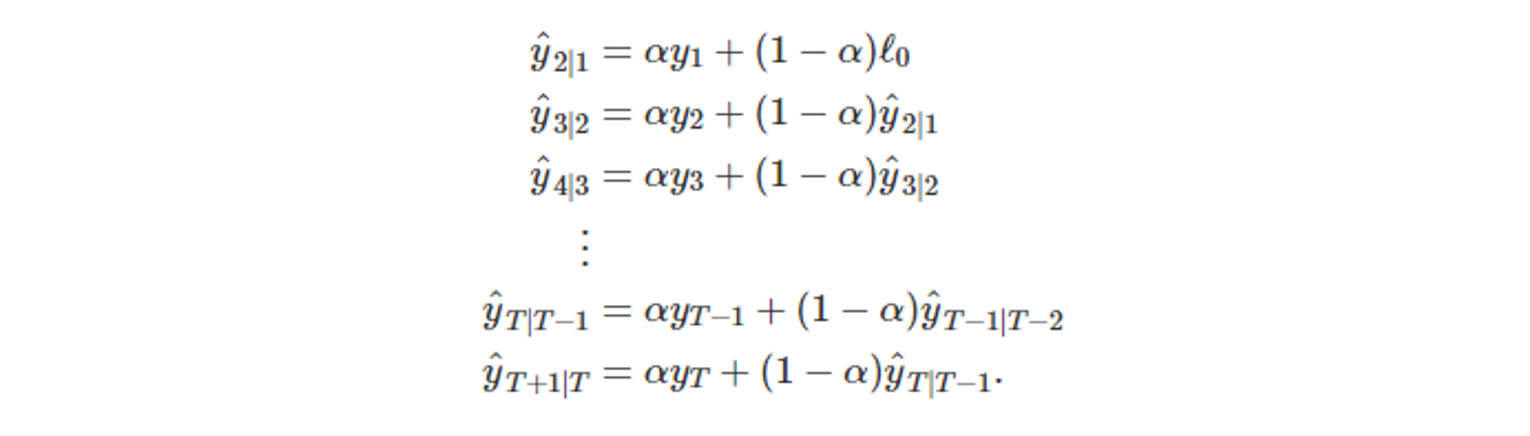
    • 해당 식을 풀어 쓰면 아래와 같다.
      
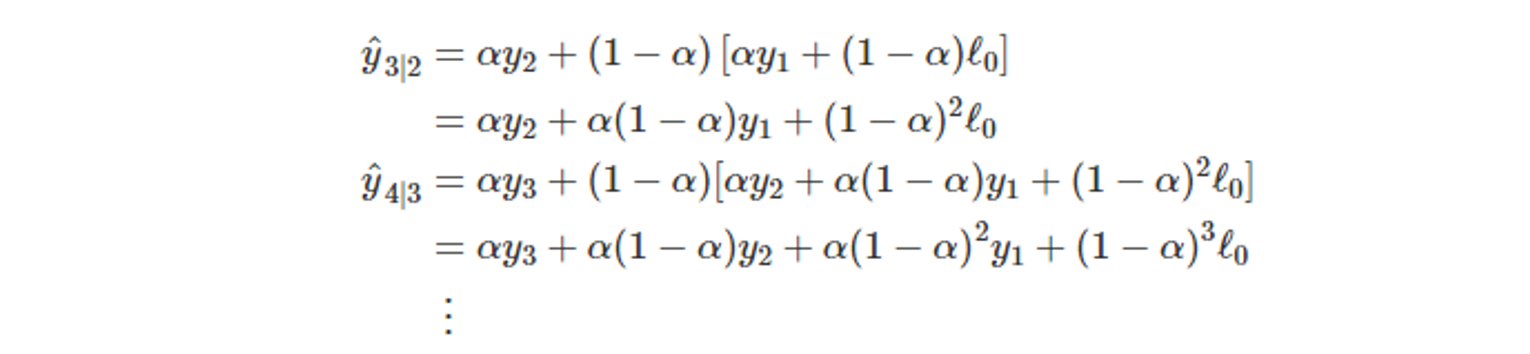
    • 아래는 식을 일반화 한 형태이다.
      
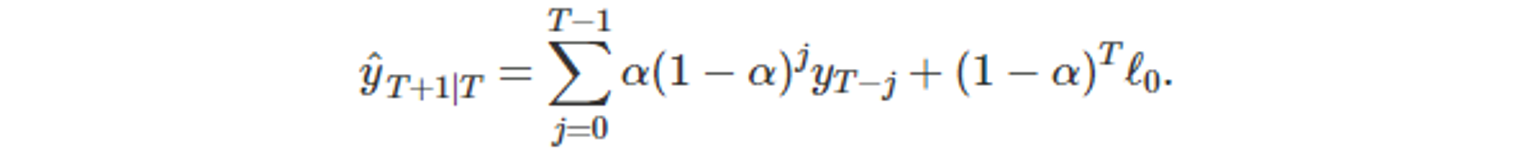
    • T가 클 수록 마지막 항의 크기가 작아진다.
      • 시계열 데이터의 길이가 길수록 첫 시점의 적합값의 개입이 작아진다.

7.1.2 성분 형태

• 단순 지수 평활 식 7.1 에 대한 다른 표현 형태
• 기법에 포함된 각 성분에 대한 Forecast equation과 Smoothing equation으로 구성된다.
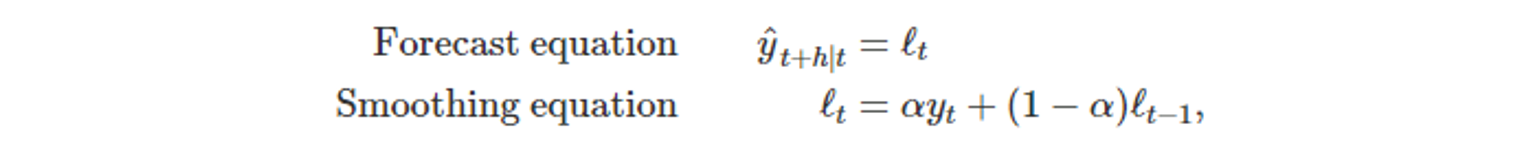
  • ℓ_t : 시간 t에서 시계열의 수준식, 수준값(가중치에 의해 평활화된 값)
    • 단순 지수평활에서 포함된 유일한 성분이다.
  • Smoothing equation
    • 각 시기 t에서 시계열의 추정된 수준을 얻을 수 있다.
• 성분 형태는 자주 사용하지 않지만, 다른 성분을 추가할 때 쉽게 사용할 수 있는 형태이다.

7.1.3 평평한 예측값

• 단순 지수 평활은 평평한 예측함수를 가진다.
  • 즉, h가 몇이든 모든 예측값이 마지막 수준값과 같은 값을 갖는다.
  • Why? 이건 one-step-forecast 이기 때문에
• 이러한 예측은 시계열에 추세나 계절 성분이 없을 때 사용할 수 있다.

7.1.4 최적화

• 단순 평활 지수를 사용하기 위해
  평활 매개변수 α 와 초기값 ℓ_0 가 필요하다.
• 최적의 α 를 선정하는 방법
  모든 t에 대한 예측값을 산출하고, 그에 대한 잔차를 최소화 하는 α 를 선정한다.
  

7.1.5 예제 : 사우디 아라비아의 원유 생산량

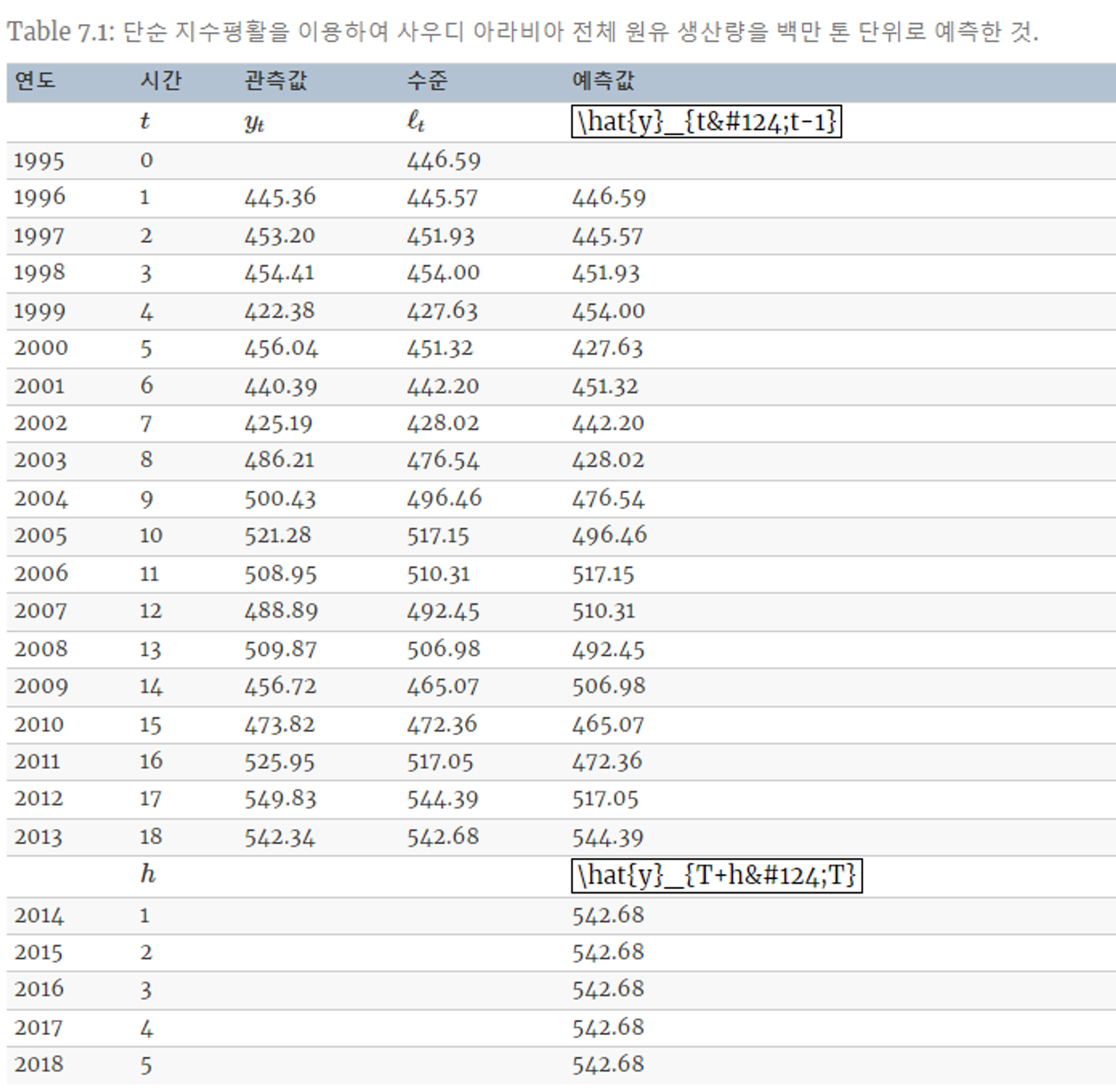
• t = 1, 2, … , 18에 대해 관측값 y_t와 적합값 ℓ_t 의 SSE를 최소화하는 α 를 산출한다.
• 이를 기반으로 미래(2014~2018)의 원유 생산량을 예측한다.
  • t=18 에서의 적합값이 이후 모든 시점의 예측값이다. (Why? [7.1.3 평평한 예측값])