온라인 Forecasting 교재 [Forecasting : Principles and Practice] 7장 2절을 참고하여 작성하였습니다.
7.2 추세 기법
7.2.1 Holt의 선형 추세 기법
- 추세가 있는 데이터를 예측할 수 있도록 단순 지수 평활을 확장한 기법이다.
- Forecast equation과
두 개의 Smoothing equation (하나는 수준에 관한 것, 다른 하나는 추세에 관한 것)을 포함이다.
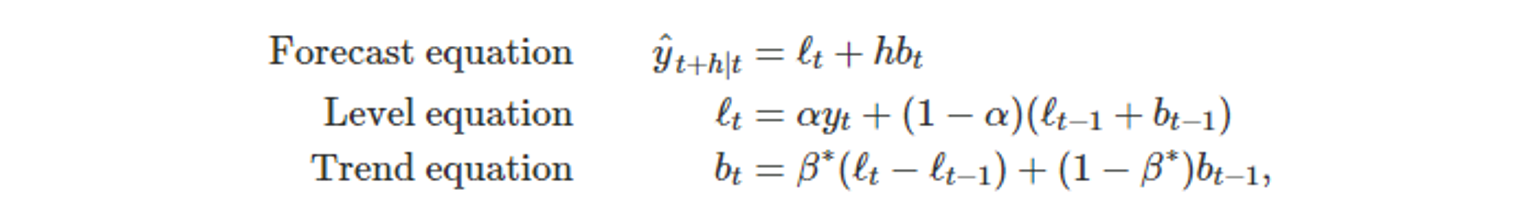
- ℓ_t : 시간 t에서 추정한 수준값, 수준식
- b_t : 시간 t에서의 시계열의 추세(기울기) 추정 값
- α : 수준에 대한 평활 매개변수
- β∗ : 추세에 대한 평활 매개변수
- β∗이 작다는 것은 기울기가 시간에 따라 변하기 어려움을 의미한다.
- Level equation(수준식)
- 수준값 ℓ_t 은 관측치 y_t 의 가중 평균이다.
- (ℓ_t-1 + b_t-1)으로 시간 t에 대한 one-step-ahead 학습 예측임을 알 수 있다.
- Trend equation(추세식)
- 추세값 b_t는 이전에 추정된 수준값(ℓ_t - ℓ_t-1)과 추세값(b_t-1)을 기반으로
시간 t에서 추정한 추세의 이동 평균이다.
- 추세값 b_t는 이전에 추정된 수준값(ℓ_t - ℓ_t-1)과 추세값(b_t-1)을 기반으로
- 예측값이 추세를 가지고, 평평하지 않다.
- h단계 앞의 예측은 선형 함수 형태이다.
- 마지막 시점에서 추정한 수준값(ℓ_t)에
마지막 시점에서 추정한 추세값(b_t)과 h를 곱한 값을
더한 값이다.
- 마지막 시점에서 추정한 수준값(ℓ_t)에
7.2.1.1 예제 : 항공객
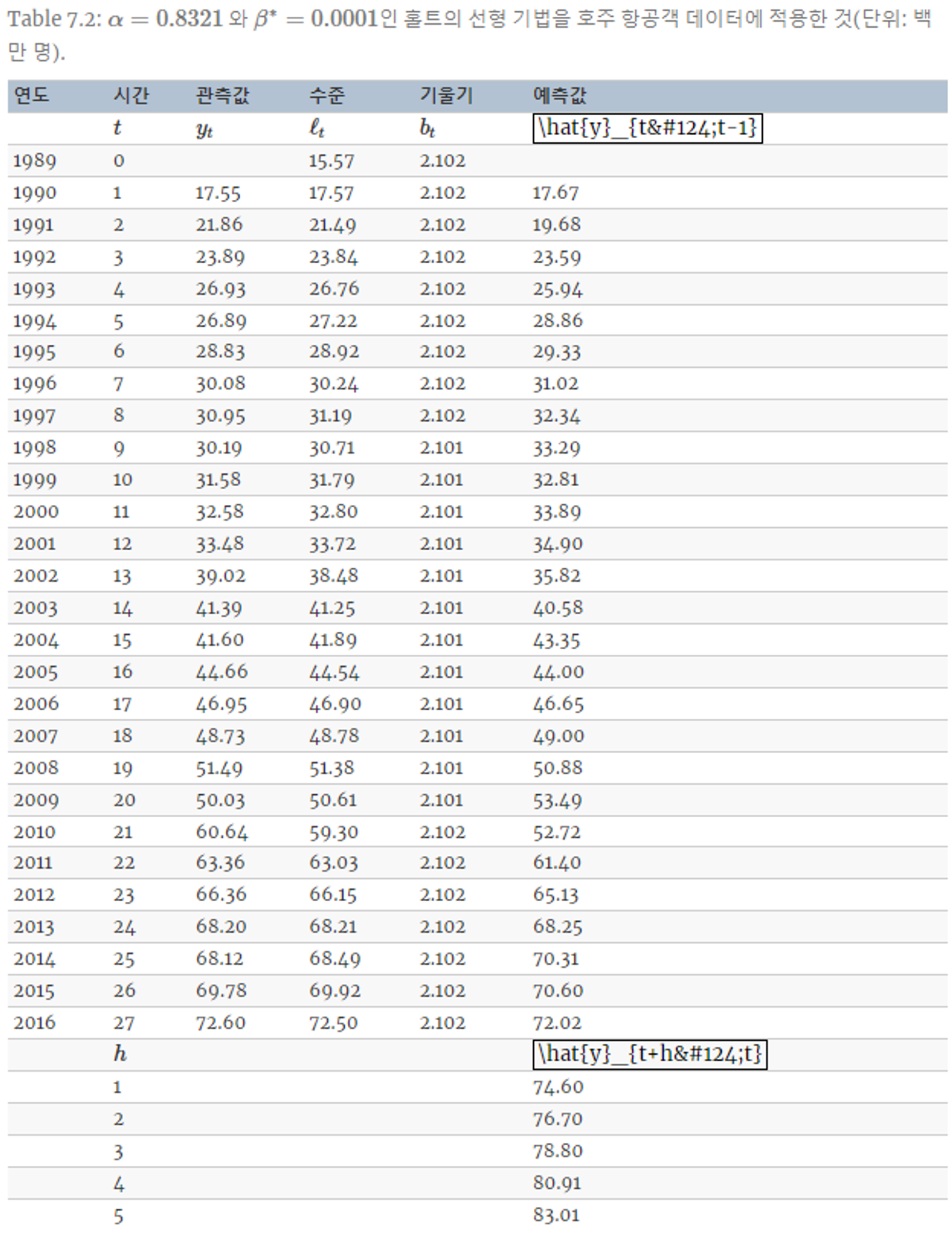
7.2.2 Gardner & McKenzie의 감쇠 추세 기법
- 홀트(Holt)의 선형 기법 : 미래에도 계속 일정한 (증가 또는 감소) 추세가 존재한다.
- 이는 과도하게 예측하는 경향일 수 있고, 예측 범위(forecast horizon)이 늘어날수록 더 심해진다.
- 이를 해결하고자 미래 어느 시점에 추세를 평평하게 감쇠시키는 한 가지 매개변수를 도입하였다.
- 추세 감쇠 효과를 보이며, 시계열 자동 예측 분야에서 가장 인기있는 기법이다.
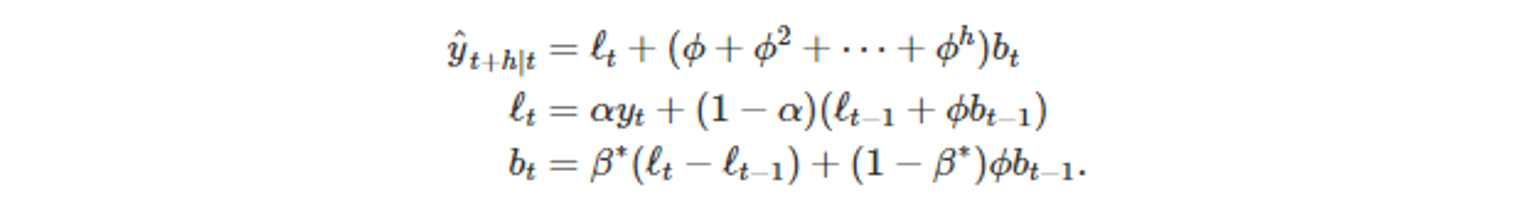
- ϕ : 감쇠 매개변수
- 추세를 감쇠시켜, 미래 어떤 시점에 추세가 상수가 되도록 한다.
- ϕ가 작을수록, 추세 감쇠 효과가 크다.
- 실제 상황에서 ϕ가 0.8보다 작은 경우는 거의 없다.
- ϕ = 1 일 때, Holt의 선형 기법과 동일하다. (비-감쇠 모델)
⇒ ϕ는 보통 최소 0.8 최대 0.98로 둔다. - h→∞일 수록 예측치 y_hat_t+h|t 를 산출할 때, 추세에 곱해지는 값은
ϕ + ϕ^2 + … + ϕ^h* 에서 ϕ / (1-ϕ) 가 된다.- 단기 예측값에서는 추세, 장기 예측값에서는 상수로 표현하기 위함이다.
- ϕ : 감쇠 매개변수
