GPTQ 리뷰

Intro

scaling law에 따라 모델의 성능은 파라미터의 개수에 따라 더 증가하는 경향을 보이면서 자연스럽게 LLM의 발전으로 이어져왔다. 다만, 이런 초거대 모델은 그 사이즈 자체로 많은 해결해야 할 문제점을 보여줬다. 학습을 시키기 위해선 어마어마한 양의 GPU 자원을 필요로 하고 모델 가중치를 불러와 서비스하기에도 파라미터의 양은 너무 컸다. 따라서, 모델을 나누어 학습 시키거나, 압축하는 방법론이 대두되기 시작했고, 이 방법들으 그 사이 많은 발전을 이루었다.

GPTQ는 그 가운데 현재 LLM을 압축하는 데에 가장 활발히 쓰이는 알고리즘 중 하나이다. 그리고 스터디 팀원들과 함께 리뷰했던kaggle AIMO 1st solution에서도 사용 되었기에 호기심을 가지고 논문 리뷰를 진행했다.

GPTQ 들어가기에 앞서

Post Traing Quantization

모델을 압축하는데는 크게 두 가지 방법론이 있다.

1. 재훈련을 하여 모델의 크기를 압축하는 것.
2. 훈련 후에 작은 데이터 조각으로 one-shot을 진행하여 압축하는것.(Post-Training-Quantization)

전자의 방법론으로는 대표적으로 pruening이 있고, 후자의 대표적인 방법으로는 llm.int8() 과 같은 양자화 기법이 있다.

GPTQ는 후자인 PTQ에 속한다.

Optimal Brain Quantization

GPTQ는 OBQ(Optimal Brain Quantization)의 방법론을 좀 더 최적화한 기법이다. GPTQ와 OBQ의 핵심 아이디어는 quantization 결과에 대해 목적 함수를 적용하는 것이다.

${argmin_{\hat{W}}=||WX - \hat{W}X||^2_2}$

$W$는 원래의 weight을 말하고 $X$는 input, $\hat{W}$는 양자화 된 weight을 말한다. 즉 일종의 MSE 로스를 적용하는 것이라고 할 수 있다.

그리고 위의 함수 식에서 얻을 수 있는 Hessian을 사용하여 최적화에 활용한다. Hessian은 함수의 각 변수에 대해 2계 도함수를 모아 행렬의 형태로 만들어 둔 것을 말한다.

• Hessian Wiki
• Hessian 계산 과정

위의 식에서 우리가 가장 관심있는 항은 $\hat{W}$이다. 이 때의 Hessian 은 $H = 2X_FX_F^{\top}$이다.

OBQ의 알고리즘

OBQ는 pruneing과 quantization의 방법론을 섞은 것으로, 먼저 에러를 최소화하는 방향으로 양자화를 진행한 후에, 후에 양자화 될 가중치들을 업데이트한다. 이는 양자화가 된 이후에 생길 loss를 minimum하게 조정하기 위함이다. 이는 두 가지 식으로 표현 가능하다.

a. $w_q = argmin_{w_q} \frac{(quant(w_q) - w_q)^2}{[H_F^{-1}]_{qq}}$

b. $\delta_F = \frac{w_q - quant(w_q)}{[H_F^{-1}]_{qq}}\cdot(H^{-1}_F)_{:,q}$

$w_q$는 row안의 weight이고, F는 양자화 될 32bit의 가중치를 의미한다. $[H_F^{-1}]_{qq}$ 는 $H$의 역행렬의 대각 원소를 의미한다. 이 때, 한 번에 하나의 weight만을 양자화하면서 진행한다.

매 계산 시마다, H를 새로 계산하게 되면 연산의 복잡도가 매우 커지므로, H의 복잡도를 줄이기 위한 방안이 제시되어 있다.

c. $H^{-1}_{-q} = (H^{-1} - \frac{1}{[H^{-1}]_{qq}}H^{-1}_{:,q}H^{-1}_{q,:})_{-q}$

q 번째 가중치에 대한 업데이트가 종료되고 나서 q번째 행과 q 번 열을 삭제함으로써(Gausian Elimination) H에 대한
계산의 효율성을 높일 수 있다고 한다.

덧붙여 사족으로 a의 식은 상당히 흥미로운데, 왜냐하면 함수에 대한 이계도함수의 매트릭스가 함수의 결과값을 나누고 있는 모양새이기 때문이다. 뉴턴랩슨 방식에서 쓰이는 $\frac{f(x)}{d f(x)}$ 의 느낌으로 함수를 근사하기 위한 공식과 매우 비슷한 모습을 띄기 때문이다. 이 식이 정확하게 무엇을 의미하는지는 얕은 수학 지식으로 인해 알 수 없었지만, 결국 quantization 자체가 작은 오차를 유지하며 가중치의 근사값을 생성해내는 과정이라는 맥락과 연결지어서 생각해본다면 결국 최적의 근사값을 찾는 식이라고 이해할 수 있을 것 같다.

GPTQ

위의 OBQ는 좋은 성능을 보여주는 양자화 기법이었으나, 모델이 커질 수록 계산 복잡도가 증가하여, LLM과 같은 큰 모델에 적용하기에는 무리가 있었다고 한다. GPTQ는 이 부분을 해결하여 GPTQ는 BLOOM과 같은 165B 사이즈의 모델도 4시간의 one-shot만 있으면 양자화가 가능할 수 있도록 하였다.

Arbitrary Order Insight

OBQ는 모든 원소들을 greedy한 순서로 양자화를 진행 하지만, 실제로는 무작위적인 순서로 양자화를 한 것과 큰 차이가 없었기 때문에, 한 번에 모든 row를 같은 순서로 양자화를 진행했다고 한다. 이 때의 결과는 OBQ로 진행했을 때와 큰 차이가 없었다고 한다. 아래는 계산의 진행 방식을 보여주는 그림이다.

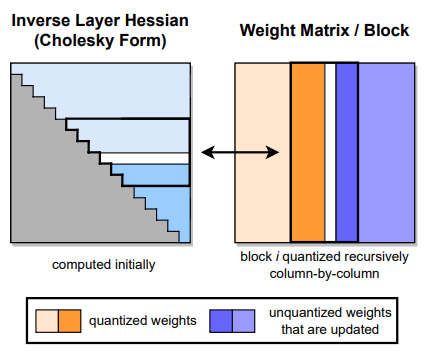
Lazy Batch-Updates

위의 방식대로 진행을 하더라도, 메모리에 접근하는 비율이 낮고, 현대적인 GPT의 계산 성능을 다 이끌어 낼 수 없기 때문에 속도가 드라마틱하게 증가하진 않는다고 한다.

이때, 마지막 $column_i$가 rounding 될 때 영향을 끼치는 것은 해당 칼럼에 적용된 updates만 영향을 끼친다는 사실을 발견했고 이로써 '게으른 배치'가 가능했다고 한다. 이를 $B=128columns$로 두고 블록 내의 모든 계산이 끝난 후에 한꺼번에 $H^{-1}$에 적용했다고 한다.

이 방법은 전체적인 계산의 총량을 줄여주진 않지만 계산의 병목현상을 줄여줌으로써 계산 속도를 높여준다고 한다.

Cholesky Reformulation

마지막으로는 양자화 계산의 결과의 수치적인 정확도를 올리기 위한 방법이다. 특히, 전 단계와 깊은 연관이 있다. 전 단계의 작업은 때때로 $H^{-1}$를 정의불가능하게 할 수 있다는 점이다. 이는 남아있는 가중치를 엉뚱한 방향으로 업데이트하게 한다. 이러한 현상은 모델이 클 수록 빈번하게 발생한다.

작은 모델에서는 dampening을 하여 $H$의 대각성분에 작은 상수를 더함으로써 해결할 수 있지만, 큰 모델에서는 충분하지 않았다.