Deep Learning: 역전파(BackPropagation) 이해하기

출처

역전파(BackPropagation) 이해하기

인공 신경망이 순전파 과정을 진행하여 예측값과 실제값의 오차를 계산하였을 때 어떻게 역전파 과정에서 경사 하강법(Gradient Descent)을 사용하여 가중치를 업데이트하는지 직접 계산을 통해 이해해봅시다.

1. 인공 신경망의 이해(Neural Network Overview)

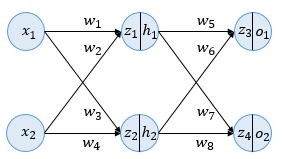
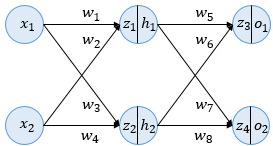
이번 예제에서 사용할 인공 신경망은 다음과 같습니다.

• 층 구성: 입력층(Input Layer), 은닉층(Hidden Layer), 출력층(Output Layer)

• 뉴런 수: 입력층 2개, 은닉층 2개, 출력층 2개

• 활성화 함수: 시그모이드(Sigmoid) 함수

• 편향(Bias): 고려하지 않음

• 각 뉴런의 입력값(가중합)은 이전 층의 모든 출력값에 해당 가중치를 곱한 후 더한 값입니다.
  • 이 값은 시그모이드 함수를 거치기 전의 상태이며, 활성화 함수의 입력값이라고 부릅니다.
• 시그모이드 함수를 통과한 값은 뉴런의 최종 출력값입니다.

이번 목표: 모든 가중치 $w$를 역전파로 업데이트

2. 순전파(Forward Propagation)

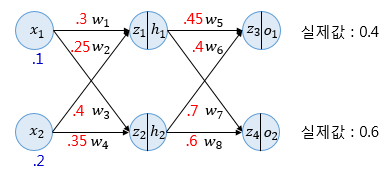
순전파는 입력값이 각 층을 거쳐 출력층까지 전달되는 과정입니다.

1. 입력층 → 은닉층

   • 각 입력값 $x$에 해당 가중치 $w$를 곱하고, 은닉층 뉴런별로 합산하여 $z_1, z_2$ 계산

   • $h_1 = \sigma(z_1)$, $h_2 = \sigma(z_2)$

2. 은닉층 → 출력층

   • 은닉층 출력값 $h_1, h_2$에 해당 가중치 $w$를 곱하고 합산하여 $z_3, z_4$ 계산

   • $o_1 = \sigma(z_3)$, $o_2 = \sigma(z_4)$

3. 오차 계산

   • 손실 함수: 평균 제곱 오차(MSE)

   • $E_{o1} = \frac{1}{2}(target_{o1} - output_{o1})^2$

   • $E_{o2} = \frac{1}{2}(target_{o2} - output_{o2})^2$

   • $E_{total} = E_{o1} + E_{o2}$

3. 역전파 1단계(BackPropagation Step 1)

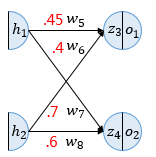
• 출력층과 은닉층 사이의 가중치를 업데이트하는 단계입니다.

• 업데이트 대상: $w_5, w_6, w_7, w_8$

예시: $w_5$ 업데이트

연쇄 법칙(Chain Rule) 적용

• 연쇄 법칙(Chain Rule)은 합성 함수의 미분을 구하는 규칙으로, 한 변수의 변화가 중간 변수를 거쳐 다른 변수에 영향을 줄 때 각 단계의 변화율(미분값)을 곱해 최종 변화율을 계산하는 방법입니다.
• 신경망에서는 출력 오차가 여러 층을 거쳐 가중치에 연결되므로, 가중치가 오차에 미치는 영향을 구할 때 연쇄 법칙을 적용해 오차 → 활성화 함수 출력 → 가중합 → 가중치 순으로 각 단계의 미분을 곱해 최종 기울기(gradient)를 얻고, 이를 경사 하강법으로 가중치를 업데이트합니다.

1. 첫 번째 항

2. 두 번째 항 (시그모이드 미분)

3. 세 번째 항

4. 곱

5. 가중치 업데이트 ($\alpha = 0.5$)

4. 역전파 2단계(BackPropagation Step 2)

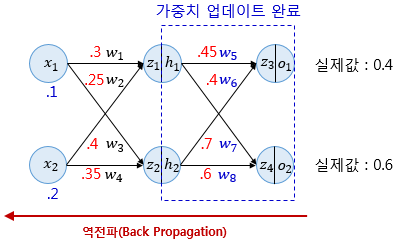
• 은닉층과 입력층 사이의 가중치를 업데이트하는 단계입니다.

• 업데이트 대상: $w_1, w_2, w_3, w_4$

예시: $w_1$ 업데이트

1. $h_1$의 오차 기여도

2. 시그모이드 미분

3. 입력값

4. 곱

5. 가중치 업데이트

5. 결과 확인

• 업데이트된 가중치로 다시 순전파를 수행하여 오차 감소 여부를 확인합니다.

• 은닉층 입력: $z_1 = 0.07979778$, $z_2 = 0.10988248$

• 은닉층 출력: $h_1 = 0.51993887$, $h_2 = 0.52742806$

• 출력층 입력: $z_3 = 0.43126996$, $z_4 = 0.67650625$

• 출력층 출력: $o_1 = 0.60617688$, $o_2 = 0.66296548$

• 오차: $E_{o1} = 0.02125445$, $E_{o2} = 0.00198189$

• 전체 오차: $E_{total} = 0.02323634$

기존 오차 $0.02397190$ → 업데이트 후 오차 $0.02323634$
$\Rightarrow$ 오차 감소 확인 ✅

참고

1. 시그모이드 함수

• 인라인: $h = \sigma(z) = \frac{1}{1 + e^{-z}}$

2. 순전파(Forward Propagation) 계산

• 입력에서 은닉층으로

  $z_1^h = w_{1,1} x_1 + w_{2,1} x_2$

  $z_2^h = w_{1,2} x_1 + w_{2,2} x_2$

• 활성화 값

  $h_1 = \sigma(z_1^h)$

  $h_2 = \sigma(z_2^h)$

3. 은닉층에서 출력층으로

• $z_1^o = w_{1,1}^o h_1 + w_{2,1}^o h_2$

• $o_1 = \sigma(z_1^o)$

4. 손실함수(예: MSE)

• $Loss = \frac{1}{2} \sum_{i=1}^2 (t_i - o_i)^2$

5. 역전파 계산 예시

• 경사하강법에 의한 가중치 업데이트

  • 목표: 계산된 기울기를 이용해 가중치를 조정

  • 이 단계에서야 비로소 가중치 값이 변경됨

  $w \leftarrow w - \eta \frac{\partial Loss}{\partial w}$

• 연쇄법칙(chain rule) 사용

  • 목표: 가중치가 손실(Loss)에 얼마나 영향을 주는지를 계산

  • 이 단계에서는 아직 가중치를 바꾸지 않고, 오직 "변화율"만 구함

  • 여기서 $o$는 뉴런의 출력, $z$는 가중합(활성화 함수 입력)

  $\frac{\partial Loss}{\partial w} = \frac{\partial Loss}{\partial o} \cdot \frac{\partial o}{\partial z} \cdot \frac{\partial z}{\partial w}$