[Hands-On Machine Learning] 2장 한눈에 보는 머신러닝 🕕

2. 머신러닝 프로젝트 처음부터 끝까지

머신러닝 주택 회사

• 목표: 캘리포니아 인구조사 데이터를 바탕으로 캘리포니아의 주택 가격 예측 모델을 개발.

• 데이터 특징

  • 캘리포니아의 블록 그룹(block group) 단위별로 인구, 중간 소득, 중간 주택 가격 등의 데이터를 포함.

  • 블록 그룹: 미국 인구조사국에서 사용하는 최소한의 지리적 단위로, 보통 600~3,000명의 인구를 포함.

  • 모델 작업: 제공된 데이터를 바탕으로 구역(block group)의 중간 주택 가격을 예측.

2.2.1 문제 정의

1. 비즈니스 목표 이해

   • "회사에서는 이 모델을 어떻게 사용하고, 이를 통해 어떤 이익을 얻으려고 하는가?"를 이해해야 함.

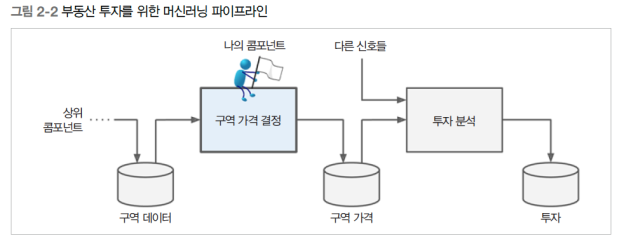
   • 예: 모델 출력(예측된 주택 가격)이 다른 머신러닝 시스템의 입력으로 사용되어 해당 지역의 투자 가치 여부를 판단.

2. 현재 솔루션 이해

   • 현재는 전문가들이 수동으로 구역 특성을 분석해 주택 가격을 추정.

   • 정확도가 낮고, 비용과 시간이 많이 소요됨.

   • 대신, 캘리포니아 인구조사 데이터를 활용하면 효율적이고 더 정확한 예측 가능.

3. 문제 유형 정의

   • 지도 학습(Supervised Learning): 레이블(중간 주택 가격)이 제공됨.

   • 회귀 문제(Regression): 값을 예측해야 하며, 다변량 회귀(multivariate regression)에 해당.

   • 배치 학습(Batch Learning): 데이터가 일정하며, 변경 사항이 빈번하지 않으므로 배치 학습 방식이 적합.

2.2.2 성능 측정 지표 선택

• 목적: 모델이 얼마나 잘 작동하는지 분석할 수 있는 성능 지표를 선정.

1. 평균 제곱근 오차 (RMSE)

• 정의: 예측값과 실제값 간의 오차 제곱의 평균값에 제곱근을 취한 값.

• 특징

  • 오차에 민감하며, 큰 오차일수록 더 큰 영향을 미침.

  • 모델의 오류를 직관적으로 파악 가능.

• 활용: 회귀 문제에서 가장 일반적인 성능 평가 방법.

2. 평균 절대 오차 (MAE)

• 정의: 예측값과 실제값 간의 절대 오차의 평균값.

• 특징

  • 이상치(outliers)에 덜 민감.

  • RMSE와 비교하면 큰 오차의 영향이 줄어듦.

• 활용: 이상치가 많을 때 유용.

3. 노름(Norm)

• 정의

  • RMSE는 유클리디안 노름$(\ell_2)$에 해당하며, 우리가 익숙한 거리 계산에 해당.

  • MAE는 맨해튼 노름($\ell_1$)에 해당하며, 절댓값의 합 계산.

• 선택 기준

  • RMSE는 이상치에 민감.

  • MAE는 이상치가 많을 때 더 안정적.

2.2.3 가정 검사

가정을 확인하는 목적

• 지금까지 설정한 가정을 다시 확인해보는 과정으로, 문제를 정의하는 데 있어 심각한 오류를 조기에 방지하기 위함.

확인할 가정 예시

1. 출력 데이터 활용 방식

   • 시스템이 예측한 주택 가격이 하위 시스템의 입력으로 사용되며, 실제 값(숫자)을 그대로 사용.

   • 만약 하위 시스템이 이를 카테고리("저렴", "보통", "고가")로 변환한다면, 문제 정의를 회귀 → 분류 문제로 변경해야 함.

2. 추가 확인 필요성

   • 관련 팀(하위 시스템 담당자)과 대화 후 올바르게 가정을 검증.

   • 예: 실제 가격 데이터를 그대로 사용한다는 점을 확인 → 회귀 문제로 유지.

결론

• 목표 정의: 캘리포니아 지역에 기반한 중간 주택 가격 예측 모델 개발.

• 문제 정의

  • 지도 학습, 다변량 회귀 문제.

  • 배치 학습 방식.

• 성능 지표

  • RMSE를 주 성능 지표로 사용하며, 이상치에 따라 필요시 MAE도 고려.

• 가정 확인

  • 모델 출력 데이터가 하위 시스템에서 실제로 어떻게 사용되는지 확인.

• 모든 준비가 끝났으면, 이제 코딩 단계로 진입할 수 있음.