Wilson Score Interval 기반 보정 오류율(e)

https://www.statisticshowto.com/wilson-ci/

Wilson Score 기반 보정 오류율(e) 계산 요약

• Wilson Score Interval은 비율 추정을 보다 안정적으로 만들기 위해 관측 오류율 $f$ 대신 보정 오류율 $e$ 을 사용한다.

  • 특히 표본 크기 $N$ 이 작을 때 효과가 크다.

1. 보정 오류율 공식(Wilson Score Lower Bound 기반)

• Wilson Score를 오류율에 적용한 식은 다음과 같다.

• $N$ = sample size

• $f$ = observed error rate

• $z$ = z-score (기본 (z = 0.69), 약 50% 신뢰도)

이 식은 Wilson Score의 “lower bound”에서 유도된 보수적 오류율 추정이다.

2. 예시 값

• 표본 크기: $N = 20$

• 관측 오류율: $f = 0.15$

• z-score: $z = 0.69$

3. 단계별 계산 과정

1) z2 계산

$z^2 = 0.69^2 = 0.4761$

2) 중심값 보정 항

따라서

3) 루트 내부 계산

(a)

(b)

(c)

합산:

루트 적용:

4) z 곱하기

5) 분자 계산

6) 분모 계산

7) 최종 보정 오류율

4. 결과 해석

• 관측 오류율: $f = 0.15$

• Wilson Score 기반 보정 오류율: $e \approx 0.2132$

• 즉, 표본 크기가 작기 때문에 오류율이 실제보다 낮게 추정될 가능성을 보정해 더 큰 오류율을 반환한다.

  • 이는 overfitting을 방지하기 위해 더 안전한 추정을 제공한다.

5. 오류율 보정 공식(e)이 표본 크기 N에 따라 어떻게 변하는지를 시각화

• 관측 오류율 $f = 0.15$ (점선)

• Wilson Score 기반 보정 오류율 $e$ (실선)

• 표본이 작을수록 보정 오류율이 더 크게 나타난다

• 표본이 커질수록 $e \to f$

아래는 생성에 사용한 전체 코드이다.

Python 코드 (수식 + 시각화 포함)

import numpy as np
import matplotlib.pyplot as plt

def corrected_error(f, N, z=0.69):
    z2 = z**2
    numerator = f + z2/(2*N) + z*np.sqrt((f/N) - (f**2)/N + z2/(4*N**2))
    denominator = 1 + z2/N
    return numerator/denominator

# fixed observed error rate
f = 0.15

# sample sizes
Ns = np.arange(5, 201, 5)
values = [corrected_error(f, N) for N in Ns]

plt.figure(figsize=(8,5))
plt.plot(Ns, values, label="Corrected Error (e)")
plt.axhline(f, linestyle="--", label="Observed Error (f)")
plt.xlabel("Sample Size (N)")
plt.ylabel("Error Rate")
plt.title("Corrected Error Rate vs Sample Size")
plt.legend()
plt.grid(True)
plt.show()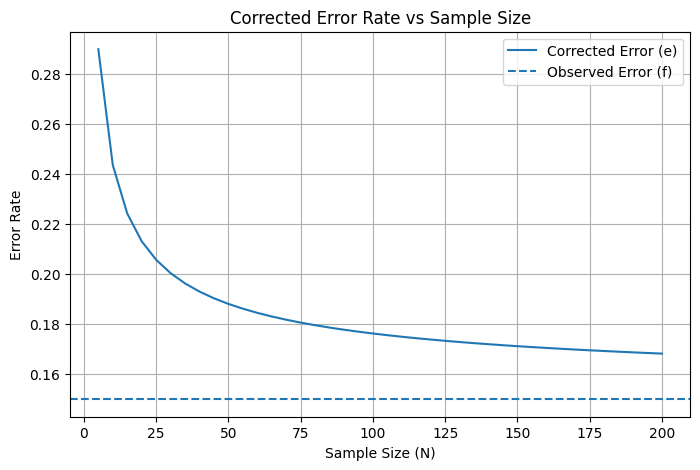

• Wilson Score 기반 보정은 작은 표본에서 과도하게 낙관적인 Error Rate 추정을 방지함

• $N$ 이 커지면 보정 오류율 = 관측 오류율에 가까워짐

• Decision Tree의 pruning 또는 모델 비교에서 매우 유용함