적응형 선형 뉴런, ADALINE

적응형 선형 뉴련 ADAptive LInear NEuron (아달린 ADALINE)

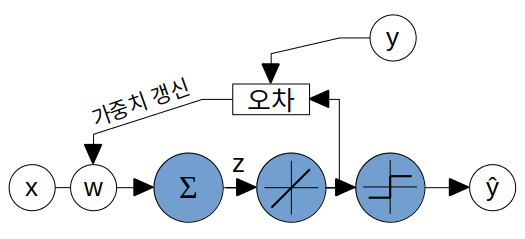
퍼셉트론의 개선 버전 - 가중치 업데이트 방식 개선

퍼셉트론은 가중치 변화량에 대한 식($\Delta\boldsymbol{w}=\eta(y-\hat{y})\boldsymbol{x}$)을 정의하여 가중치를 업데이트했지만 아달린의 경우 미분 가능한 목적함수를 정의하고 그래디언트를 이용해 목적함수를 최소화하는 방향으로 가중치를 업데이트한다.

• 목적함수?
  • 손실함수 loss function: 개별 샘플의 $y$와 $\hat{y}$의 오차를 계산하는 함수.
  • 비용함수 cost function: 전체 샘플의 loss function 값의 합.
  • 목적함수 objective function: 모델, 뉴런 학습시에 최소화 또는 최대화하려는 함수. 목적함수를 최소화 또는 최대화하는 방향으로 모델의 가중치를 변화시키므로 모델 학습의 방향을 제시해주는 역할. 종종 비용함수가 목적함수를 대신하기도 한다.

아달린의 비용함수 (목적함수) - 제곱오차합 SumSquaredError

$J(\boldsymbol{w})=\frac{1}{2}\sum_i(y^{(i)}-\phi(z^{(i)}))^2$

여기서 $\phi$는 선형함수로 입력값과 출력값이 같다. $\phi(z)=z$
즉, 아달린은 실제 클래스 레이블 $y=\pm1$과 실수값 $z$를 비교한다.

$J$는 미분 가능한 함수이고 볼록함수이므로 그래디언트의 반대 방향으로 변수값을 조절하면 $J$의 값이 작아지게된다. $J$의 값이 작아질수록 $y=+1$인 샘플의 $z$값은 1에, $y=-1$인 샘플의 $z$값은 -1에 가까워지는 경향을 보일 것이다.

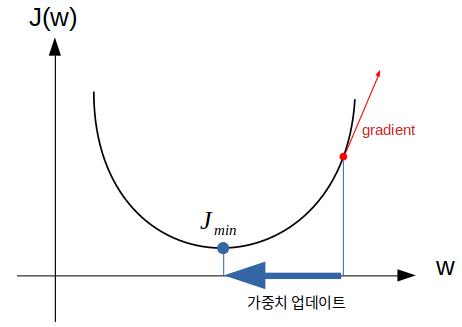
경사 하강법 gradient descent

비용함수가 제곱오차합으로 제곱오차합을 최소로 만드는 방향으로 가중치 학습이 진행되어야한다.
그러기 위해서는 위의 그림처럼 비용함수를 가중치에 대해서 미분한 그래디언트 반대 방향으로 가중치를 업데이트한다.
이를 경사 하강법이라 한다.

$\boldsymbol{w} = \boldsymbol{w} + \Delta \boldsymbol{w}$
$\Delta \boldsymbol{w} = -\eta\nabla J(\boldsymbol{w})$

$\nabla J(\boldsymbol{w})=-\sum_{i}(y^{(i)}-\phi(\boldsymbol{w^\top x}^{(i)}))\boldsymbol{x}^{(i)}$

$\boldsymbol{w} = \boldsymbol{w} + \Delta \boldsymbol{w} = w + \eta\sum_{i}(y^{(i)}-\phi(\boldsymbol{w^\top x}^{(i)}))\boldsymbol{x}^{(i)}$

퍼셉트론의 경우 샘플 하나당 한번 가중치 업데이트를 했었는데 아달린은 모든 샘플을 계산 후 가중치 변화량을 합산하여 가중치 업데이트한다. 이렇게 주어진 훈련 샘플 전체를 기반으로 한번의 업데이트를 진행하는 방식을 배치 경사 하강법 batch gradient descent이라 한다.

코드

https://github.com/canlion/ml_study/blob/main/1_adaline.ipynb

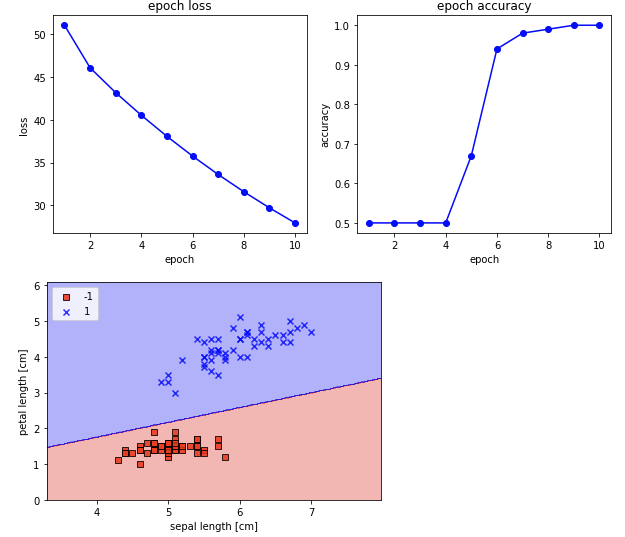
특성 스케일링 feature scaling

대부분의 머신러닝 알고리즘들은 최고 성능을 위해 데이터 전처리가 필요.

🤔: 예를 들어 두개의 특성 $\boldsymbol{x}_1, \boldsymbol{x}_2$를 입력으로 삼는 경우, $\boldsymbol{x}_1$의 범위가 $\boldsymbol{x}_2$의 범위보다 훨씬 크다면 $z$값을 일정 수준, 아달린의 경우 $\pm 1$에 근접하게 맞추기 위하여 $w_{1}$을 매우 작게, $w_{2}$를 크게 만들어야 할 것이다. 그에 따라 비용 함수 $J$는 다음과 같이 그려지고 최소값을 향한 경로가 복잡해진다.
🤔: $\Delta \boldsymbol{w} = \eta\sum_{i}(y^{(i)}-\phi(\boldsymbol{w^\top x}^{(i)}))\boldsymbol{x}^{(i)}$이면 $\Delta w_1, \Delta w_2$은 같은 에러*학습률에 각각 $x_1, x_2$를 곱한 값. $x_1$의 값의 범위가 $x_2$에 비해서 아주 크다면 $\Delta w_1, \Delta w_2$의 크기에도 차이가 생긴다. 매우 큰 $\Delta w_1$을 줄이기위해 학습률을 줄이면 $\Delta w_2$값이 너무 작아져 학습이 느려지고, 반대로 학습률을 높이면 너무 큰 $\Delta w_1$값으로 $w_1$학습이 어려워진다?

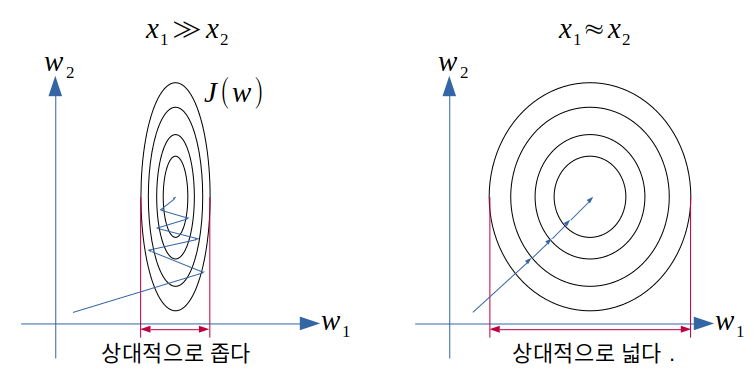
• 표준화 standardization: 데이터를 정규 분포화.
  $\boldsymbol{x}=\frac{\boldsymbol{x}-\mu}{\sigma}$
  
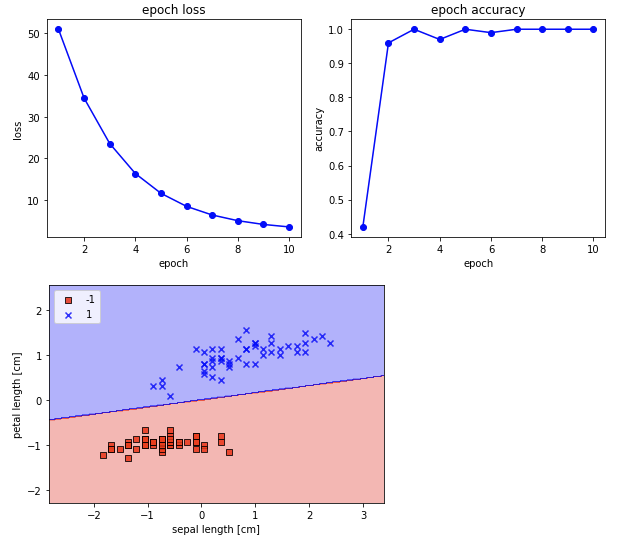
  🤔: 손실함수값 감소와 정확도 향상이 빠르다.

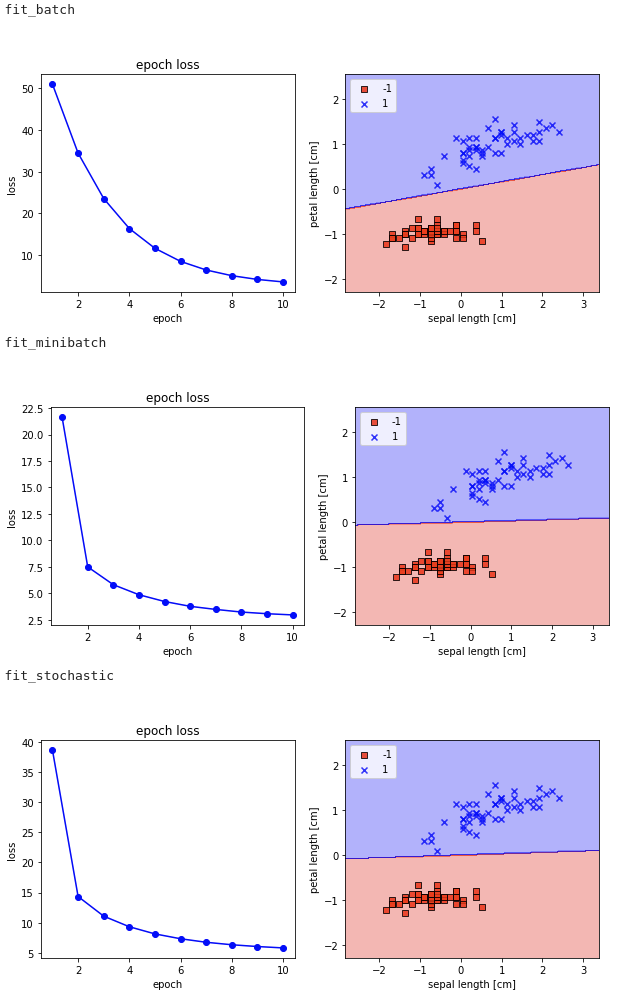
배치/미니배치/확률적 경사 하강법

• 배치 경사 하강법
  • 전체 훈련 샘플을 한 번 순회할 때마다 한 번의 가중치 업데이트
  • 전체 훈련 샘플을 모두 고려한 가중치 갱신
  • 샘플이 너무 많은 경우 학습이 느림

• 확률적 경사 하강법 stochastic gradient descent
  • 하나의 샘플마다 한 번의 가중치 업데이트
  • 배치 경사 하강법보다 가중치 업데이트가 자주 일어나 학습이 빠름
  • 비용함수값의 변화가 배치 경사 하강법보다 어지러움
  • 비용함수의 지역 최솟값을 탈출하기 쉬움
  • 사용
    • epoch마다 훈련 샘플 셔플
    • 학습률은 epoch이 증가할수록 작아지게 설정

• 미니 배치 경사 하강법 mini-batch gradient descent
  • 배치 경사 하강법과 확률적 경사 하강법의 절충안
  • 전체 훈련 샘플의 묶음마다 한 번의 가중치 업데이트
    • ex) 훈련 샘플 32개에서 그래디언트를 누적하여 한 번 가중치 업데이트
  • 비교
    • 배치 경사 하강법보다 가중치 업데이트가 자주 일어나 학습이 빠름, 비용함수의 지역 최솟값 탈출에 유리
    • 확률적 경사 하강법의 개별 샘플 연산을 벡터화시켜 연산 효율 증가, 여러 샘플을 고려한 가중치 갱신