본 포스트는 서울대학교 데이터사이언스를 위한 머신러닝 및 딥러닝 2 이상학 교수님 수업과 수업 자료를 기반으로 작성하였습니다.
 **무단 베포 금지**
 그동안 MLDL2의 수업의 흐름을 되짚어 보면 실제의 확률 분포를 그래프를 통해 해석하려는 Bayesian Network를 공부하고 이를 활용해 clustering을 수행하는 GMM, sequantial data에 hidden variebles를 도입한 HMM을 공부하였다.
 오늘 역시 BN의 종류 중 하나인 Markov Random Fields와 Conditional Random Fields에 대해 공부할 것인데 이들은 Undirected Graph를 활용한다는 점이 GMM, HMM과 다르다. 레츠고

1. Introduction/Representation

1.1 Directed vs. Undirected Models

 서론에서 언급했다시피 사용하는 graph의 성질이 이전 모델들과 다른데 방향성이 있는 경우 node를 화살표로 연결하지만, 방향성이 없으면 그냥 직선으로 연결한다. 실제 데이터에는 순서가 있는 데이터(weather data 등)와 순서가 없는 데이터(image의 pixel)가 모두 존재한다.
 그래서 순서가 없는 경우 우리는 undirected graphical models을 사용할 것이고(줄여서 UGMs) 같은 용어로 봐도 무방한 Markov Random Fields(줄여서 MRFs)는 statiscal physics에서 유래되었다.

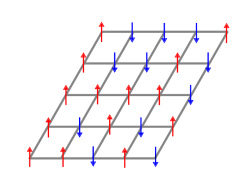
- 통계적인 기법으로 물체의 자성을 판단하는 Ising model
 UGM은 pariwise relationships을 갖고, specific configuration에 대해 score하는 것을 위주로 알아보겠다.

1.2 Undirected Graphical Models: Applications

 UGM이 해결하는 task에는
1. Image Segmentation and Semantic Labeling
2. Pose estimation
3. Stereo Matching(입체적인 위치 파악)
4. Denoising(노이즈 제거)
실제 pixel을 hidden variables인데 인접 픽셀 간에 강한 dependency가 존재한다 생각하고 noisy pixel이 관측되었다고 모델을 설계한다.

5. Social Network Community Detection
   등이 있다.

1.3 Representation

 UGM(a.k.a. MRF)는 분포 $P(X_1, ..., X_n)$을 나타내고 undirected graph $H$를 정의한다. 또한 positive potential funtions인 $\psi_c$를 정의하는데 여기서 c는 그래프 $H$의 cliques를 나타낸다.(뒤에서 다룰거임.)
 확률 분포와 이 positive potential functions는 다음의 관계를 지닌다.

 여기서 z는 partition function을 의미하고 식으로 쓰면

 이다. 즉, potential function은 하나의 joint configuraion에 대해 'pre-probabilistic' socre을 주는 것과 같다.(직접적인 확률은 아니지만 모든 가능한 결합 설정에 대해 정규화를 통해 확률 분포를 얻을 수 있는 기반을 기반을 마련한다. 상대적인 선호도를 표현하는 것)

1.4 Cilques

 Clique의 정의를 살펴보면

For $H=<V,E>$, a complete subgraph(clique) is a subgraph $H'=<V'\subseteq V, E'\subseteq E>$ such that nodes in $V'$ are fully interconnected.

 즉, 영어 그대로 해석하면 graph $H$내의 subgraph로 노드들이 모두 서로 연결되어 있을 때를 말한다. 또한 특이하게 노드가 없는 것도 하나의 clique로 여겨 아래 그래프에서 clique의 갯수는

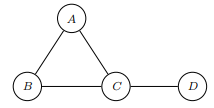
 총 10(1+4+4+1)개이다.
 그 다음 알아야될 용어는 maximal clique인데

A maximal clique is a complete subgraph s.t. any superset $V''\supsetneq V$ is not complete.

 포함할 수 있는 다른 node가 없는 clique를 maximal clieque라 한다.(위 예시에선 A-B-C, C-D)
 Clique는 반드시 고려해야하는 변수들 간의 가능한 모든 dependencies를 나타낸다.

1.5 Example UGM

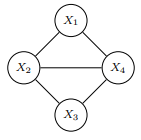
  위 그래프에서 potential functions을 계산해보면

 where $Z=\sum_{x_1,x_2,x_3,x_4}\psi_c(\mathbf{x}_{124})\cdot\psi_c(\mathbf{x}_{234})$
 다음과 같은데

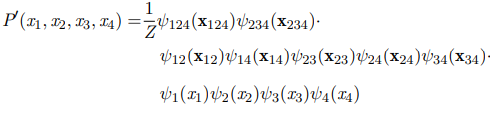
 왜 위와 같이 모든 clique에 대해 계산하지 않고 maximal clique에서만 계산하냐면 위 식에서

 로 보면 결론적으로 maximal cliques에 대한 함수로 나타낼 수 있기 때문이다.(empty set의 clique 쓰지 않는 이유도 비슷함. potential 함수는 바로 아래에서 다룰 것이다.)

1.6 Interpretation of Clique Potentials

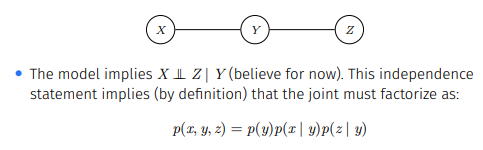
 우리는 위 확률을 $p(x, y,z)=p(x,y)p(z\mid y)=p(x\mid y)p(z,y)$로 표현할 수 있는데 결코 두 확률을 marginal 확률과 conditional 확률로 나타낼 수 없다.(예시에서는 무조건 하나씩)
 그래서 positive clique potentials은 확률이 아닌 'compatibility', 'goodness'로 보는 것이 타당하다.(확률에 비례는 하니까)
 두 atom간의 상호작용은 attractive(양수), repulsive(음수)일 수 있는데 positive clique potentials을 쓰고 싶으니 exponential form을 사용하게 되었고 $\phi_c$를 도입하여

 로 나타내었다. 이때 $\phi_c(\mathbf{x}_c)$는 real value funtion으로 편의상 potential이라고도 부른다.
 그럼 우리는 $p(\mathbf{x})$를

 로 쓰게 되고 이런식으로 나타낸 구조를 Gibbs distribution이라 한다.
 또한 지수의 sigma term을 energy로 해석할 수 있는데 여기에 -를 붙여서 enrgy가 높으면 exp값이 큰 값이 갖도록 설계되어있다.(low energy = stable = more likely)

2. Independence

2.1 Independence Properties

 The global Markov properties of a UG $H$는

 로 정의되고
 seperation in an UG는 Z를 지나지 않으면서 X에서 Y로 갈 수 있는 경로가 있는지 확인하면 된다.(Z와 연결된 edges를 제거하고 X와 Y사이 경로가 존재하는 지 보면 된다.)

2.1.1 I-maps

 우리는 Independence를 기반으로 I-maps을 정의할 수 있는데 먼저 $I(P)$는 $P$가 $V$의 distribution일 때, $I(P)$는 $P$에서 $(X\perp\!\!\!\perp Y\mid Z)$인 set을 의미한다. $H$는 graph이므로 역시 $I(H)$를 independencies의 집합으로 정의할 수 있는데 만약 $I(H)\subseteq I(P)$이면 H는 P에 대한 I-map이라 정의한다.(참고로 Bayesian Network에선, $I(G)\subseteq I(P)$였다.)

2.1.2 Hammersley-Clifford Theorem

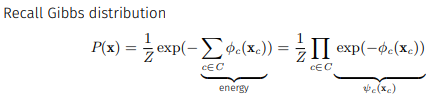
 Hammersley-Clifford Theorem은 $P$가 $V$의 positive distribution이고 $H$가 $V$의 Markov Random Fields graph일 때,
 $H$가 $P$의 I-map이라는 것과 $P$가 $H$의 Gibbs distribution으로 나타낸 것이 동치라는 것이다.
 이를 해석해보면 필요조건은 Gibbs distribution에 따라 그래프 $H$를 그리면 $H$가 $P$의 I-map이라는 것이고 충분조건은 $P$의 I-map인 $H$가 존재하면 $P$는 $H$의 cliques들로 이루어지는 Gibbs distribution으로 modeling할 수 있다는 것이다.

3. Examples

3.1 Boltzmann Machines

 Boltzman Machine은 대칭적으로 연결된 뉴런과 유사한 네트워크로 각 단위가 on or off를 확률적으로 결정하는 모델이다.
 변수들은 visible한 것들과 hidden인 것들이 있다.

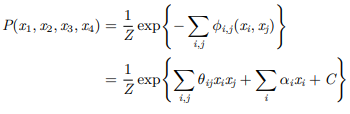
 하지만 이런 general한 Boltzman machines의 학습 알고리즘의 계산 복잡도와 효율성 때문에 learning이 비현실적인데 visible layer와 hidden layer사이의 연결만을 허용하는 Restricted Moltzman Machine(줄여서 RBM)이 고안되었다.

3.2 Restricted Boltzman Machines(RBM)

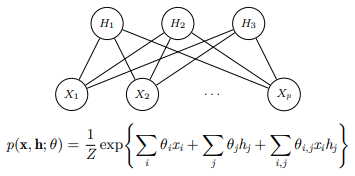
 이렇게 hidden layer과 visible layer만 연결 가능한 bipartite graph로 나타낼 수 있고 이때 distribution은 node potential과 edge potential만을 활용해서 나타낸다.
 이 때, 한 layer가 주어지고 다른 layer에 대한 conditional probability distribution은 다음과 같이 나타난다.

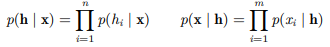
 이를 사용할 수 있는 분야에는 'Topic Modeling'이 있다.

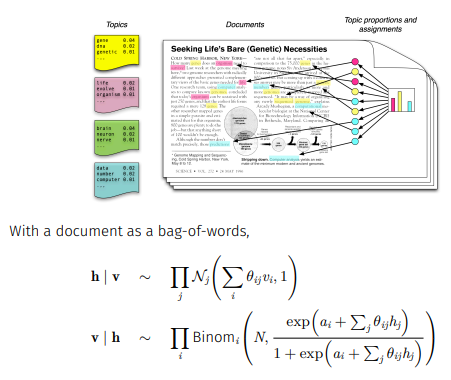
 v는 단어들의 counts를 나타내고 h는 topic을 의미한다.
 또 다른 응용으로 Deep Belief Networks가 있는데

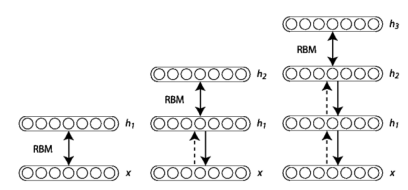
 이렇게 RBMs를 stacking한 구조로 만들어 이미지, 음성 인식과 같은 복잡한 데이터에서 패턴을 학습하는데 사용된다.

4. Conditional Random Fields

 Conditional Random Fields(줄여서 CRF)는 MRF의 conditional version인데 clique potentials을 input features가 주어진 상황에서 구한다.
 주로 sequences 데이터의 모델링에 쓰인다.(linear CRF)
 일반적인 CRF가 수행하는 tasks는 다음과 같다.

 머신러닝에는 접근법이 크게 Generative model과 Discriminative model이 있는데 Generative Model은 주어진 데이터의 생성 과정을 학습하여, 새로운 데이터 샘플을 생성하는 모델이고, Discriminative model은 주어진 입력 데이터가 어떤 카테고리에 속하는지를 결정하기 위해, 입력과 출력 사잉의 조건부 확률 분포를 학습하는 모델이다.

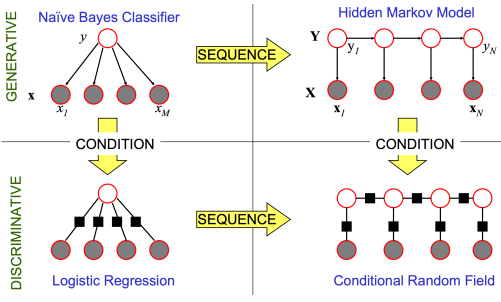
4.1 Linear Conditional Random Fields

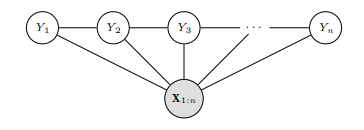
  CRF는 given Y에서 X들 사이의 independence를 가정하지 않기 때문에 다양한 임의의, 독립적이지 않은 feature를 다룰 수 있다는 flexibility의 장점이 있다.
 따라서 distribution은 다음과 같이 계산한다.

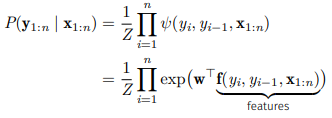
 더 general하게 작성하면

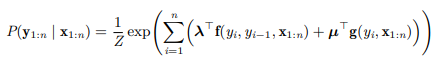
 되고 마지막 항의 edge potential을 나타낸다.
 이를 활용하여

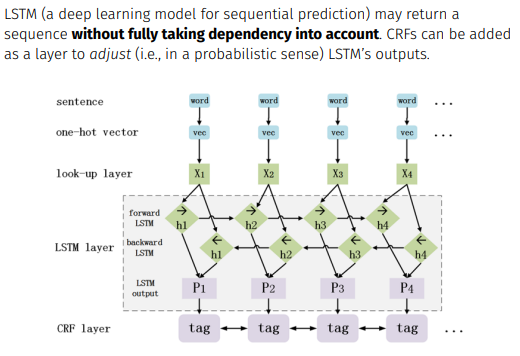
 처럼 sequantial modeling을 하고 그 아래에 CRF layer을 두어 보정된 결과를 산출하게 한다.
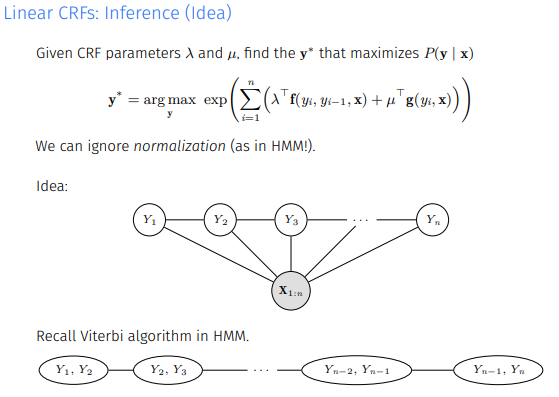
 Inference는 Idea만 간단히 얘기하면 Viterbi algo.처럼 max를 이어나가는 방식으로 학습한다.

5. 느낀점

 아무래도 최근에는 사용되지 않는 모델들이다보니 내용이 쉽게 와닿지 않는 것 같다. 사실 오늘 배운 내용은 대부분 neural network로 대체되서(괜히 딥러닝 딥러닝 그러는 것이 아니다.) 교수님도 자세히는 나가시지 않은 것 같다.
 오늘 포스트를 통해 얻어갈 점은 순서가 없는 data의 경우 undirected graph를 통해 접근한다는 점, 확률을 계산하고 비교하기 위해 potential을 정의하고 potential을 낮추는 방향으로 설계한 점 정도만 알아가도 괜찮지 않을까 싶다.
 시험이 다가오면서 과제도 많아지고 할게 쌓여가지만 할건 해야지. 이미 약속을 잡아버려서 열심히 살아가는 수밖에 없다.
 그럼 다음 시간에-