[ML] Hidden Markov Models

바서기·2024년 3월 18일

ML

목록 보기

4/5

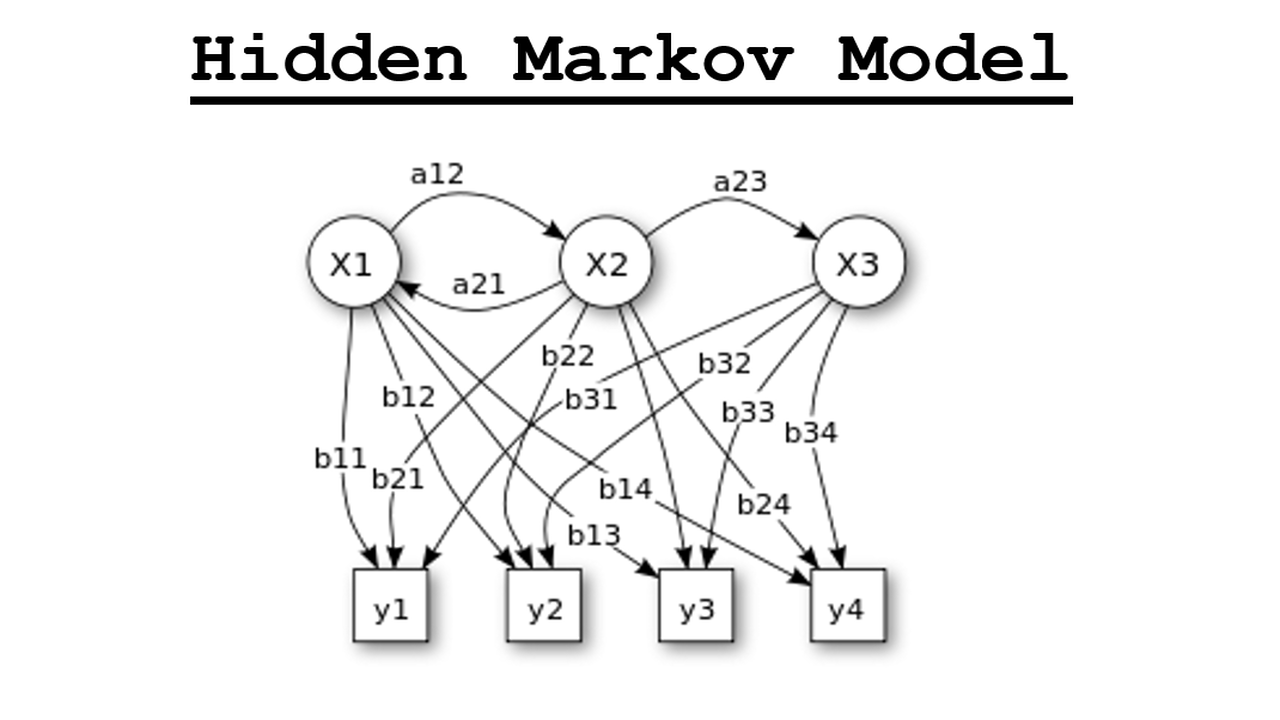
본 포스트는 서울대학교 데이터사이언스를 위한 머신러닝 및 딥러닝 2 이상학 교수님 수업과 수업 자료를 기반으로 작성하였습니다.
이번 포스트는 MLDL 2의 2번째 강의와 3번째 강의에서 다룬 내용인 Hidden Markov Models에 관한 내용이다. 작년 2학기에 들은 공학수학 2 수업에서 Markov process에 대해 처음 배웠었는데 잠시 내용을 떠올려보면...

[Review] Markov Process(공학수학 2)

$X_n$ 을 random variables(줄여서 RVs)의 sequence로 정의하고 이 때 each $X_k$ can take values only in $S=\{1, 2, ..., m\}$ 이다.
이런 정의를 기반으로 다른 내용을 또 정의할 수 있는데
1. $(X_n)$ satisfies Markov properties $\Leftrightarrow$ For any $i,j\in S$ , $n\in \mathbf{N_0}$ (0이상의 정수를 의미) $P(X_{n+1}=j\mid X_n=i_n, ..., X_0=i_0)=P(X_{n+1}=j\mid X_n=i_n)$
2. $(X_n)$ is said to be a discrete time Markov process(or chain) $\Leftrightarrow$ $(X_n)$ satisfies Markov properties. In this case, $P_{ij}=P(X_{n+1}=j\mid X_n=i)$ is transition probability. And we can define m*m matrix called transition probability matirx as $M=(P_{ij})(1\le i\le m, 1\le j\le m)$
이렇게 transition matrix를 정의하고 확률 벡터의 오른쪽에 곱해주면서 상태를 여러번 진행시켜주었다.
또한 곱해주는 matrix인 transition matrix의 갯수가 증가하게 되면 수렴 가능성이 존재하는데(항상 존재하는 것은 아님) 만약 수렴한다면 그 matrix는 행이 일정한 matrix가 된다.( $P_{i,j}$ 가 전에 i번째 상태에서 j번째의 상태로 갈 확률을 의미하니 row가 일정한다는 것은 전에 어떤 상태이든지 관계없이 j번째로 갈 확률이 동일함을 의미한다.) 그리고 이 메트릭스에서 각 행의 성분 m개를 steady-state probability, $(X_n)$ 's limiting stationary distribution(극한 안정 분포, 초기 분포에 관계없이 나중 분포는 수렴하니까)으로 정의했다.
이런 내용들을 배우고 작년 기말에 steady-state matrix를 구하는 문제를 풀었던 것 같은데 아무튼 Markov process에서 배운 내용을 요약하면
1. Markov properties는 다음 상태를 결정하는 요인은 오로지 이전 상태만 영향을 주는 성질이다.
2. i번째 상태에서 j번째 상태로 갈 확률로 정의한 transition matrix(추이 행렬)은 수렴할 수 있고 수렴하면 그 때의 확률값들이 steady-state probability, $X_n$ 의 극한 안정 분포라고 한다.
이다.
그래서 오늘은 이 Markov Chain을 활용하는 Bayesian Networks의 Special Case인 Hidden Markov Models에 대해 알아보겠다. 레츠고

1. Intro.

1.1 Markov Chain: Basic Ideas

Markov chain의 basic ideas는 다음과 같다.

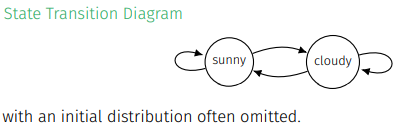
state한 상태에 들어가게 되면 initial distribution은 의미가 없는 것을 의미

discrete time from 1 to 5에서 $P(X_t\mid X_{t-1})$ 을 공유함.(except $P(X_1)$ )

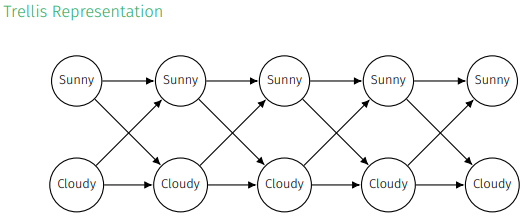
마치 격차처럼 Trellis Representation을 할 수 있고 여기서의 path는 joint assignment(특정 시점에서 변수들의 동시 할당, 위 상황에서 path sunny-cloudy-sunny-sunny-cloudy는 각 요일의 날씨가 sunny, cloudy, sunny, sunny, cloudy를 의미)를 나타냄.
또한 joint probability는 transition probabilites와 initital probability의 곱으로 설명할 수 있다.

1.2 Motivation: Markov Chains to HMM

이 chain이 Markov chain을 만족하기 위해선

Z_{t+1}\perp\!\!\!\perp(Z_1, ..., Z_{t-1})\mid Z_t

를 만족해야 함.
즉, Markov chain은 현재 상태인 $Z_t$ 가 미래에 대한 모든 정보를 가지고 있을 때 사용하는 모델인데(이런 $Z_t$ 를 complet state로 여긴다) 현실은 불완전하거나 noise가 포함된 $Z_t$ 에 대한 정보만 주어져 hidden Markov model이 필요해진다.

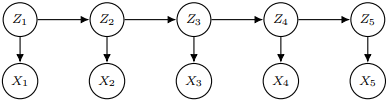
hidden Markov model(줄여서 HMM)은 위 유향 그래프를 나타내는 모델이다. Z들은 hidden states를 의미하고 X들은 sequence of observations로 우리에게 관찰되는 값들이다. 확률 분포로 표현하면

p(x_{1:n}, z_{1:n})=p(z_1)p(x_1\mid z_1)\prod_{t=2}^np(z_t\mid z_{t-1})p(x_t\mid z_t)

이다. 그리고 하나의 가정을 추가해 $Z_1,...,Z_n$ 을 discrete random variables로 유한개의 가능한 값 중 하나를 갖는다 생각해 $Z_t\in \{1,...,m\}$ 로 본다.

1.3 Hidden Markov Models 개요

이러한 HMMs는 sequantial data에 해당하는 speech, written text, genomic data, weather patterns, financial data, animal behaviors 등 다양한 data에서 강력한 modeling을 선보인다.
특히 Dynamic programming은 HMMs에 대해 tractable inference, 추적가능한 추론을 가능하게 하는데 크게
1. Viterbi algo.를 통한 hidden states에서 the most probable sequence를 찾고
2. forward-backward algo.를 통해 probabilistic inference를 하며
3. Baum-Welch algo.를 통해 parameter estimation을 한다.
예시를 들어보면

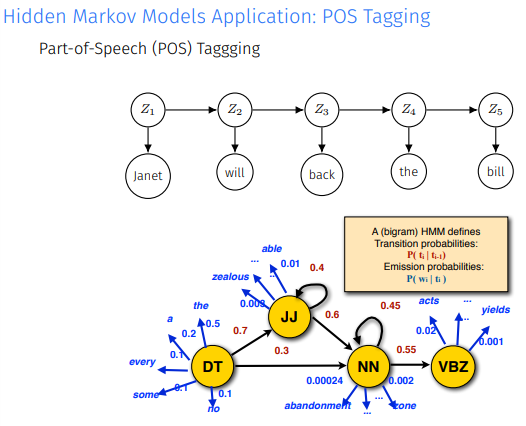
speech에서 각 단어들의 품사가 어떻게 될지 예측한다.

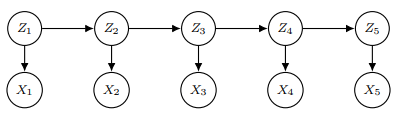
이제 HMM의 구성요소에 대해 살펴보면
가장 먼저 initial distribution $\pi$ 는 $Z_1$ 의 분포를 의미한다.

\pi_i=P(Z_i=i)

또한 Z에서 다음 Z로 넘어가는 transition probabilites와 Z에서 X로 넘어가는 emission distributions이 있는데 이 값들은 모두 time-homogeneity해 시간에 의존하지 않는다.

T_{ij}=P(Z_{t+1}=j\mid Z_t=j) \\ \epsilon_i(x_t)=p(x_t\mid Z_t=i)

여기서 T는 m*m matrix로 transition matrix를 의미. HMM의 예시를 들어보면

m=2라는 것은 Z가 2개의 states를 가질 수 있고 나머지 initial distribution, transition matrix, emission distributions가 정의된다.
HMM의 추론 과정을 말하면서 3개의 task를 말했었는데 이 내용을 수식화 하면 다음과 같다.

Decoding: given x에대해 어떤 hidden variables들의 조합이 나타날 확률이 가장 높은가? = 가장 적당한 z의 sequence는 무엇인가?
Likelihood: HMM이 주어진 경우 output sequence의 확률분포는 어떻게 되는가?
Learning: 관찰된 x를 가장 잘 설명하는 HMM의 파라미터 조합은 무엇인가?
위 세개의 tasks를 해결하는 것이 본 포스트의 최종 도착지이다!!

2. Viterbi algorithm

2.1 Viterbi algo. 개요

Viterbi algorith의 목표는

z^{\ast}_{1:n}\in \argmax_{z_{1:n}}p(z_{1:n}\mid x_{1:n})

를 찾는 것이다.
$p(x_{1:n})$ 은 이미 주어진 상수이기 때문에

z^{\ast}_{1:n}\in \argmax_{z_{1:n}}p(z_{1:n},\space x_{1:n})

로 볼 수 있다.
naive하게 계산하는 방법의 시간 복잡도를 계산하면 $O(n\cdot m^n)$ 인데 Viterbi algo.는 위 과정을 더 빠르게 가능하게 해준다.
+왜 naive한 방법의 시간복잡도가 $O(n\cdot m^n)$ 이냐면 하나의 z조합에서 확률을 계산하는데 n의 시간이 걸리고 이런 조합이 총 $m^n$ 개 있기 때문.

2.2 Think Dynamically and abstractly

argmax를 구하기 전에 max에 대해서 생각해보자.

M=\max_{z_{1:n}}p(x_{1:n},\space z_{1:n})

+ Rewriting Max Operator

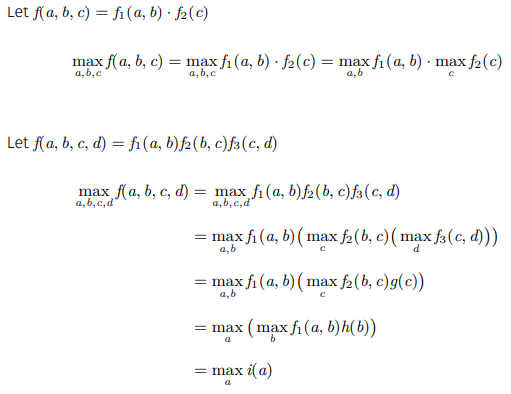
간단하게 정리해보면
- 원 함수를 변수가 관계없는 두 함수로 쪼갠 경우 각각을 최대로 만들면 된다.
- 함수를 변수를 공유하면서 여러 함수로 쪼갰을 때 초기 변수에 대한 최대값으로 볼 수 있다
여서 각각을 성질 1과 성질 2로 부르겠다.
Z의 가능한 값들 끼리 chain을 만들고

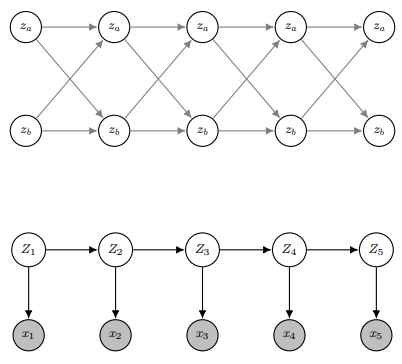
HMM과 연결하면

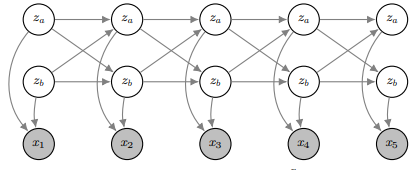
다음과 같이 되는데 우리는 given X, most probable explanation(줄여서 MPE)의 Z에 대한 score인 $\mu_t(z_t)$ 를 이렇게 정의할 수 있다.

\mu_t(z_t)= \begin{cases} p(z_1)p(x_1\mid z_1), & t=1 \\ \mu_{t-1}(z_{t-1})p(z_t\mid z_{t-1})p(x_t\mid z_t), & \text{Otherwise} \end{cases}

다음의 계산 과정을 보면 왜 score을 위처럼 정의하는지 알 수 있다.(성질1과 성질2가 반복적으로 사용됨)

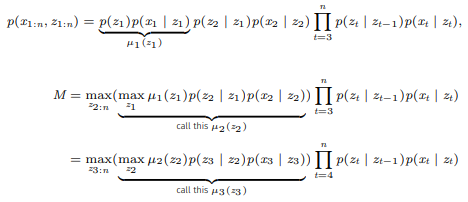
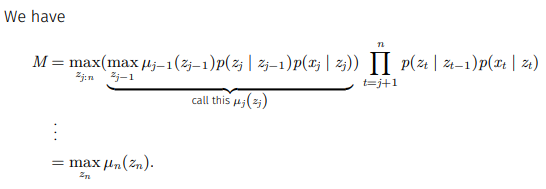
2.3 Viterbi Algorithm 원리

2.2에서 정의한 M을 다음의 알고리즘을 거쳐 계산한다.

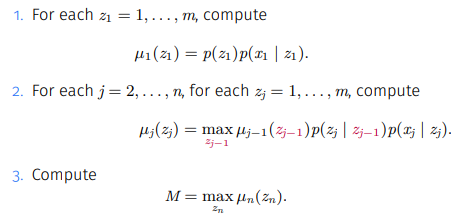
1단계에서 t=1일 때를 먼저 구하고
2단계에선 주어진 전 z에 대해 다음 z를 달리하면서 최대 값을 구한다.
3단계에선 M을 계산한다.
시간 복잡도는 1단계에서 m번의 계산을 수행하고, 2단계에서 한 z에서 $m^2$ 의 계산을 수행하므로 $(n-1)m^2$ 의 계산을 더 수행해 시간복잡도는 $O(nm^2)$ 이다.

2.4 Practical Considerations

위 방법에서 발생할 수 있는 문제가 sequence의 개수가 길어지면 probability가 거의 0에 가까워진다는 것이다. 따라서 log를 씌워 이 문제를 해결한다.

\log \max\prod=\max\prod\log

log를 l로 표현하고 $\mu_j(z_j)$ 를 $f_j(z_j)$ 로 대체하면

f_1(z_1)=l(z_1)+l(x_1\mid z_1) \\ f_j(z_j)=\max_{z_{j-1}}(f_{j-1}(z_{j-1})+l(z_j\mid z_{j-1})+l(x_j\mid z_j)

3. Forward-backward algorithm

3.1 Tasks

Forward-backward algorithm의 task의 예시는 다음과 같다.
Given $x_{1:n}$
- $P(Z_t=i\mid x_{1:n})$ for each i and each t
- $P(Z_t=i, Z_{t+1}=j\mid x_{1:n})$ for each i, j and each t
- $P(Z_t\ne Z_{t+1}\mid x_{1:n})$ for each t
구두로 설명하면
- t번째 상태의 확률 분포
- t번째와 (t+1) 상태의 결합 확률 분포
로 볼 수 있다.
기본적으로 forward-backward algorithm은 Viterbi algorithm의 first part와 유사하지만 max대신 sum을 사용하는 점이 다르다.

P(z_{1:n}\mid x_{1:n})=\frac{P(x_{1:n},\space z_{1:n})}{P(x_{1:n})}

Z에 대한 분포를 추론하기 위해선 정규화 역할을 하는 $p(x_{1:n})$ 를 계산하는 것이 중요하다.(다른 모델과의 비교를 하기 위해서)
그래서 forward-backward algorithm은 recursive fomulas를 통해 이 값을 효율적으로 계산할 것이다.(by variable elimination)

3.2 Forward-Backward Algorithm 개요

Forward-backward algorithm은 크게 2바트로 나뉜다.
1. Forward: $z_1$ 부터 $z_n$ 순으로 $p(x_{1:j},z_j)$ 를 recursive하게 계산한다.
2. Backward: $z_n$ 부터 $z_1$ 순으로 $p(x_{j+1:n}\mid z_j)$ 를 recursive하게 계산한다.
또한 forward-backward algorithm은 $O(n\cdot m^2)$ 이다.
그럼 왜 Forward Backward Probabilites라고 부를까?
Forward와 backward probabilites를 식으로 쓰면

s_t(i)=P(Z_t=i, x_{1:t}) \\ r_t(i)=P(x_{t+1:n}\mid Z_t=i)

인데 이 둘을 곱하면

s_t(i)\ast r_t(i)=P(Z_t=i, x_{1:n})

이고(given z에서 conditional independence 이용)
transition과 emission probabilites까지 고려하면

s_t(i)\ast P(Z_{t+1}=j\mid Z_t=i)\ast P( x_{t+1}\mid Z_{t+1}=j)\ast r_{t+1}(j) = P(Z_t=i, Z_{t+1}=j, x_{1:n})

를 만족한다.

3.3 Forward Algorithm: Derivation

Viteri algo.와 유사하게

s_t(z_t)= \begin{cases} p(z_1)p(x_1\mid z_1), & t=1 \\ s_{t-1}(z_{t-1})p(z_t\mid z_{t-1})p(x_t\mid z_t), & \text{Otherwise} \end{cases}

를 정의하고 식을 전개하면 다음과 같다.

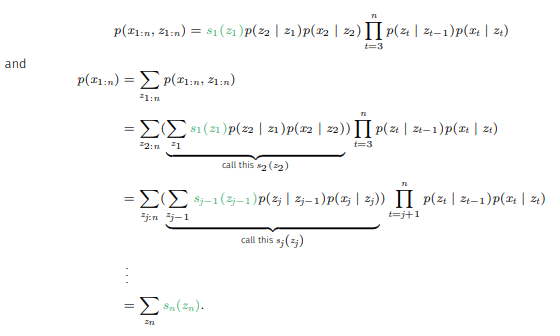
즉, forward algorithm은
1. 모든 $z_1$ 에 대해 $s_1(z_1)=p(z_1)p(x_1\mid z_1)$ 을 계산한다.
2. 모든 j(2이상)와 모든 $z_j$ 에 대해
$\sum_{z_{j-1}}s_{j-1}(z_{j-1})p(z_j\mid z_{j-1})p(x_j\mid z_j)$ 를 계산한다.
3. $p(x_{1:n})=\sum_{z_n}s_n(z_n)$
의 방식으로 작동된다.

3.4 Backward Algorithm: Derivation

Backward algorithm도

r_j(z_j)= \begin{cases} 1, & t=n \\ \sum_{z_{j+1}} p(z_{j+1}\mid z_{j})p(x_{j+1}\mid z_{j+1})r_{j+1}(z_{j+1}), & \text{Otherwise} \end{cases}

과 $P(z_1\mid z_0)=P(z_1)$ 을 정의하고 식을 전개하면 다음과 같다.

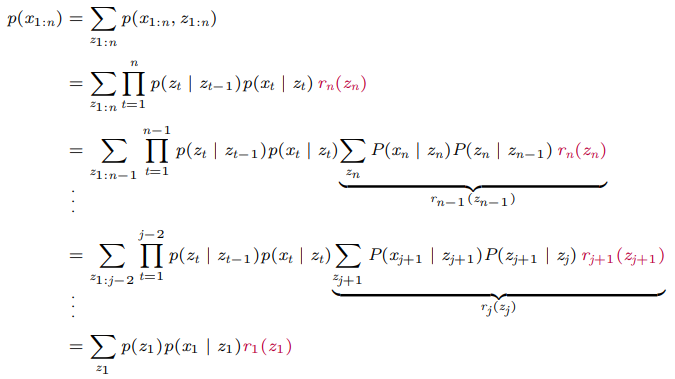
즉, backward algorithm은
1. 모든 z 값에 대해 $r_n(z_n)=1$ 로 정의한다
2. 모든 j(n-1 이하)와 모든 z 값에 대해
$r_j(z_j)=\sum_{z_{j+1}} p(z_{j+1}\mid z_{j})p(x_{j+1}\mid z_{j+1})r_{j+1}(z_{j+1})$ 룰 계산한다.
3. $p(x_{1:n})=\sum_{z_1}p(z_1)p(x_1\mid z_1)r_1(z_1)$
의 방식으로 작동된다.

3.5 Combining Forward and Backward Probabilites

이제 forward와 backward를 활용하여 추론을 해볼 것인데 $P(Z_t=i\mid \mathbf{x}_{1:n})$ 을 해보겠다.
방법은 $\mathbf{Z}$ 에서 $Z_t$ 를 summing out하는 방법을 사용할 것이다.
Forward로 $s_t(z_t)=P(z_t, \mathbf{x}_{1:t})=\sum_{z_1:t-1}P(\mathbf{z}_{1:t}, \mathbf{x}_{1:t})$
Backward로 $r_t(z_t)=P(\mathbf{x}_{t+1:n}\mid z_t)=\sum_{z_{t+1:n}}P(\mathbf{x}_{t+1:n}, \mathbf{z}_{t+1:n}\mid z_t)$
를 구한 다음

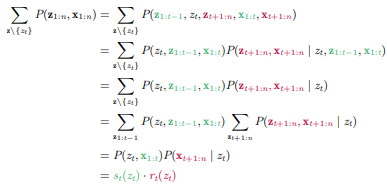
를 수행하게 된다.

3.6 (Digression) Log Sum Exp Trick

Forward and backward algorithms의 경우 확률을 구하다보니 sequence가 길어지면 arithmetic underflow or overflow 문제가 발생하게 된다.
Viterbi algorithm의 경우 log로 통해 이 문제를 해결하였지만 forward와 backward의 경우 조금 더 복잡한데 왜냐하면 log안에 합이 존재하기 때문이다.(합의 로그와 로그의 합은 다르다!)
따라서 여기서 한가지 스킬을 쓸건데 그 스킬이 바로 log-sum-exp trick이다.

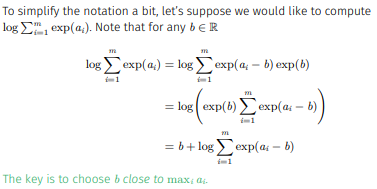
일단 시그마 안쪽의 항들을 지수 형태로 바꾸고 그 지수들 중 최댓값을 미리 빼내어 입력받는 숫자들의 범위를 control하겠다는 아이디어이다. 따라서

이렇게 forward algorithm의 식을 변환하고 최댓값을 빼낸 다음 계산을 수행한다.

4. Baum-Welch algorithm

4.1 Learning Parameters

Baum-Welch algorithm의 task는 다음의 상황에서

$\argmax_\Theta P(\mathbf{x}; \mathbf{\Theta})$ 를 찾는 것이다.
이 과정을 learning이라 표현하는데 Gaussian Mixture Model보다 복잡한 이유는 GMM의 경우 latent variable이 한 개였지만 HMM의 경우 여러 개 이기 때문이다.
$\argmax_\Theta P(\mathbf{x}; \mathbf{\Theta})$ 를 구하는데 필요한 2개의 확률인 transition probability와 emission probability를 정리하면 다음과 같다.

4.2 Transition Probability

먼저 transition probability의 식을 전개하면
Given current parameters,

P(Z_{t+1}=j\mid Z_t=i)\text{ for any t} \\\space \\ =\frac{\sum_{t=1}^{n-1}\hat P(Z_t=i, Z_{t+1}=j\mid \mathbf{x}_{1:n})}{\sum_{t=1}^{n-1}\hat P(Z_t=i\mid \mathbf{x}_{1:n})}

인데 분모는 emission probability의 분자와 같아 분자를 먼저 계산하고 분모를 계산해보겠다.
그런데 $\hat P(Z_t=i, Z_{t+1}=j\mid \mathbf{x}_{1:n})$ 는 3.2에서 forward와 backward probabilities의 응용으로 계산해두어 식을 가져오면

P(Z_t=i, Z_{t+1}=j, x_{1:n}) = s_t(i)\ast P(Z_{t+1}=j\mid Z_t=i)\ast P( x_{t+1}\mid Z_{t+1}=j)\ast r_{t+1}(j)

이 성립하고 예시를 들어 도식화하면

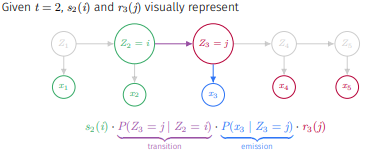
와 같다.

4.3 Emission Probability

Emission Probability의 식을 전개하면
Given current parameters,

P(X_{t}=k\mid Z_t=i)\text{ for any t} \\\space \\ =\frac{\sum_{\text{t such that }x_t=k}\hat P(Z_t=i\mid \mathbf{x}_{1:n})}{\sum_{t=1}^{n-1}\hat P(Z_t=i\mid \mathbf{x}_{1:n})}

이고 $\hat P(Z_t=i,\mathbf{x}_{1:n})$ 를 마찬가지로 forward와 backward probabilities로 계산하면

P(Z_t=i, x_{1:n})=s_t(i)\ast r_t(i)

이고 예시를 들어 도식화하면

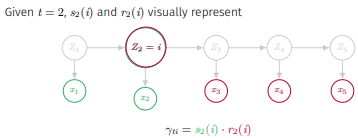
이다.

4.4 Baum-Welch Algorithm

즉, Baum-Welch Algorithm은
1. Initialize parameters
2. Repeat until convergence

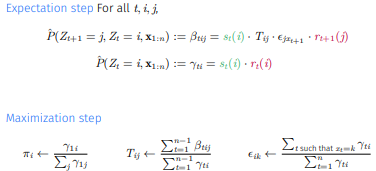
으로 작동한다.

4.5 Summary

- HMM은 sequential data에 latent states를 도입하여 모델링하는 모델이다.
- 효율적인 inference를 위한 계산 방법(variable elimination)으로 Viterbi algo.와 F-B algo.가 있다.(각각의 목적은 most proabable elimination과 likelihood이다.)
- 파라미터를 학습하기 위한 Baum-Welch algorithm은 Expectation과 Maximization steps으로 이루어진 E-M method이다.

5. 느낀점

오늘은 Markov Chain을 실생활에 적용하기 위해 hidden variables을 도입한 HMM에 대해 알아보았다. 요즘 문득 드는 생각이 이 Hidden Markov Model처럼 인생을 살아는게 나쁘지 않아보인다.(잠을 많이 안자서 정신이 나갔나?)
무슨 말이냐면 Markov Model의 핵심인 Markov properties는 미래에 영향을 주는 것은 과거가 아닌 오로지 현재 상태임을 의미한다. 즉, 우리가 살아갈 때 과거에 대해 후회보단 현재에 집중해야 더 나은 미래를 살 수 있다고 해석한다는 것이다.
물론 과거 데이터를 통해 모델의 조건부 확률을 수정하는 것처럼 과거를 돌아보는 것도 중요한 일이다. 하지만 과거에 갇혀 현재와 미래를 제한하는 것보다 현재를 통해 더 나은 미래를 꿈꾸는 것이 어떨까? 뭔가 새벽 감성같아서 부끄럽지만 아무튼 현재에 집중해 살아가고 싶다!

바서기

인생 법칙 1. 기준 낮추기 않기 2. 일단 해보기 3. 긍정 마인드