ML에 대한 공부를 하면서 느낀 점은 기본서만으로 모델을 정확히 이해하기에는 한계가 있다는 것이다. 또한 그저 패키지를 불러오고 하이퍼 파라미터들을 입력하는 것은 누구나 할 수 있는 작업이기 때문에 더 성장하기 위해선 추가적인 노력이 필요했다.(심지어 어떤 데이터에서 어떤 모델이 좋은지도 모르고 단지 최신 모델인 LGBM을 주로 사용하였다.) 그래서 ML 모델에 대해 조금 더 깊게 공부해 보기로 했고 트리 계열 모델에서 Decision Tree, Random Forest 다음의 모델인 XGBoost를 먼저 공부하게 되었다.
주로 방식은 XGBoost의 클래스를 불러와서 코드를 뜯어보거나 XGBoost 성능 및 용도에 대해 수학적인 접근(표현이 맞는지 모르겠지만 단순히 사례에 관한 논문이 아닌 왜 효율적인가 같은 질문등으로 접근하는 논문을 의미함)을 하는 논문에 대한 리뷰를 진행할 것이다.(참고로 본인의 영어 실력의 수준이 그리 높지 않아 대부분의 단어도 번역할 예정)
먼저, XGBoost: A Scalable Tree Boosting System에 대한 리뷰이다. 본 논문은 Tianqi Chen과 Carlos Guestrin가 2016년에 작성한 페이퍼로 제목의 scalable은 easy to make larger, more powerful로 해석하는 것이 좋을 것 같다.
+논문의 모든 것을 이해하는 것이 목표이고 수학적인 technique도 많으며 수식도 많아 post가 나눠져 올라갈 예정
Abstract
<단어>
end-to-end: 끝과 끝을 붙여
state-of-the-art: 최첨단의
novel sparsity-aware algorithm(본문에서 자세히 다룰 예정)
weighted quantile sketch(Appendix에서 자세히 다를 예정)
approximate tree learning ..?
cache access patterns: cache는 컴퓨터의 임시 저장소이고 cache access patterns은 이 캐시에 접근하는 방법을 의미함.
sharding: 일부 노드만을 사용해 병렬적으로 동시에 여러 개 트랜잭션을 처리, 확장성 확보와 효율성을 높이기 위한 방법
<내용>
본 논문은 novel-spasity-aware algorithm과 weighted quantile sketch를 소개하고 cache access patterns에 대한 data compression, sharding을 제안한다. 이러한 결과로 XGBoost는 기존 시스템에 비해 적은 자원으로 확장된다.
1. INTRODUCTION
<단어>
malicious: 악의 있는
used in practice: 실전에 사용되다
gradient tree boosting = GBM(gradient boosting machine) or GBRT(gradient boosted regression tree)
benchmark: 상대적인 성능 측정을 목적으로 프로그램을 실행하는 행위
incorporate into: ~에 통합되다.
de facto: 사실상의
outperform: 능가하다
configure: (컴퓨터의) 환경을 설정하다
consensus: 합의된
parallel: 병렬의
<내용>
머신러닝과 데이터로부터 유도하는 접근은 많은 분야에서 중요해졌다. 이 과정에서 두가지 중요한 factors가 있는데 usage of statistical models와 scalable learning systems이다.
XGBoost는 대회에서 높은 성능을 보이고 있음.
XGBoost의 성능은 확장 가능성으로부터 비롯되는데 이는 몇가지 중요한 system과 algorithmic optimizations에 기인한다. XGBoost를 통한 발전으로 sparse data를 다루는 a novel tree learning algorithm, approximate tree learning에서 instance weights를 다루게 해주는 theoretically justified weighted quantile sketch procedure이 있다. Xgboost는 병렬의 분산된 computation, out-of-core computation을 사용해 계산 속도가 매우 빠른편.
본문에서 말하는 내용을 정리하면
1. a highly scalable end-to-end tree boosting system
2. weighted quantile sketch
3. novel sparsity-aware algorithm
4. effective cache-aware block structure
이다.
2. TREE BOOSTING IN A NUTSHEEL
Section 2에선 gradient tree boosting algorithm을 리뷰하고 reguralized objecture를 통한 improvements를 구현할 계획.
2.1 Regularized Learning Objective
<단어>
additive function: 가산함수, arithmetic function such that whenenver positive integers a and b are relatively prime, f(ab)=f(a)+f(b)
<내용>
tree ensemble model에서 data set이 n examples와 m feature로 주어지면 데이터는 다음과 같이 표현 가능하다.
D = {(xi, yi)} (|D| = n, xi ∈ R^m, yi ∈ R)
그럼, model의 output은
이고
이 때 는 여서 space of regression trees로 CART로 알려져 있다.
T: tree leaves의 갯수
q: 각 tree의 structure에서 해당하는 point를 tree의 인덱스로 매핑해주는 함수
: tree structure q와 leaf weight w에 대응
: Decision tree와 다르게 regression tree는 각 leaf에 대응되는 score을 가지고 있는데 이 녀석이 i번째 leaf의 스코어임.
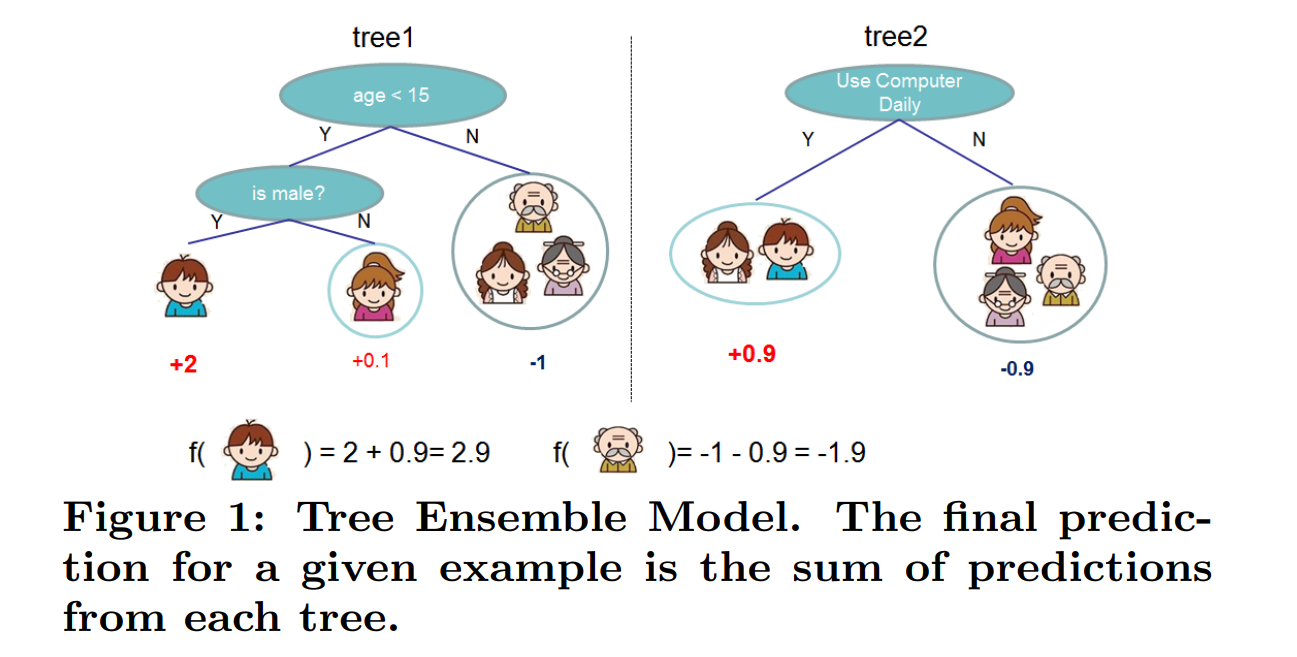
즉, 위 그림처럼 예측할 때 각 tree에 대한 예측의 sum으로 예측하는 것임.
** CART(Classification And Regression Tree)
CART는 트리를 만드는데 쓰이는 알고리즘으로 ID3 알고르즘과 비슷한 시기에 개발되었다.
불순도는 Gini index로 측정하는데 모든 조합에 대해 Gini index를 계산 한 후, Gini index가 가장 낮은 지표를 찾아 분기함.
또한 분기 시 여러개의 자식 노드가 아닌 단 두개의 노드로 분리하고 회귀 트리의 경우 불순도가 아닌 오차를 분기 지표로 사용
또한 sklearn이 사용하는 알고리즘임.
그럼 여기서 목적함수를 정의할 것인데(minimize할 대상)
l: 미분가능한 conves loss function
: model의 복잡도의 페널티를 부여하는 term, 최종 weight의 over-fitting을 막아주는 용도
이를 통해 간단하면서 예측력이 있는 모델을 갖게 된다.
2.2. Gradient Tree Boosting
<단어>
additive manner: 가산 방식, gradient boosting의 핵심 idea
greedily: 탐욕스럽게, 알고리즘에선 '현재 상황에서 최대한 이득을 내는 방향으로'의 의미
impurity: 불순도, 얼마나 다른 데이터들이 모여 있는가
<내용>
2.1에 나온 tree ensemble model의 equation은 우리 가 예측하는 함수인 y를 파라미터로 포함하기 때문에 Euclidean space에서 traditional optimization methods로 최적화를 진행할 수 없다. 따라서 대안을 마련하기 위해 첫번째로 additive manner를 적용해 iteration이라는 새로운 변수를 도입하고 점차 개선해 나가는 식으로 y를 정의하게 된다. 를 t번째 iteration에서 예측한 i번째 instsance로 생각하고 t번째 iteration에서 가장 많이 개선된 값을 라 하면 2.1의 equation을 다음과 같이 쓸 수 있다.
이 식에서 가 의미하는 바는 t번째 iteration에서 가장 많이 개선이 되는 tree를 의미한다.
또한 위 식을 쉽계 계산하도록 Second-order approximation을 진행해주면
** Second order approximation
우리가 아는 테일러의 2차 근사식으로 아주 작은 dx에 대해서 다음과 같이 쓸 수 있다.
위에서 말한 2차 근사식에서 x가 이고 dx가 으로 보면 위식이 이해가 될 것이다.
위 식에서 simplify하기 위해 constant term인 (t-1)번째의 loss function(t번째 iteration에서 이 값은 이미 결정된 값이기 때문)을 제거해주면
으로 볼 수 있게 된다.
이제 를 leaf j에 해당하는 instance의 set으로 정의하고 를 2.1에서 정의한 대로 확장해주면 equation을 다음과 같이 쓸 수 있다.
convex인 loss function이기 때문에 optimal weight of leaf j는
이고 최적화된 loss function의 값은
가 되어 우리는 위 함수를 scoring funtion으로 쓸 수 있게 되었다.

이렇게 우리는 각 leaf의 gradient와 second order gradent statistics만을 계산해서 각 leaf에서 scoring을 할 수 있고 더 작은 loss값을 만드는 구조를 선택하면 되었다.
하지만 이렇게 모든 tree 구조에서 위 값을 계산해 최적의 tree 구조를 구하는 것은 비현실적이기 때문에 greedy한 방법으로 맨 처음 한 개의 leaf에서 시작하여 점점 이득이 되는 분할만 하는 방식으로 진행되는데 을 split이후 left와 right nodes의 instance sets이라 가정하고 라 하면 split한 이후 loss funtion의 변화에 대한 식은 다음과 같다.
위 식이 어떻게 생겨났는지 알아보면 loss funtion은 작으면 작을 수록 좋으니 split하기 전의 optimal value에서 split한 후의 optimal value를 뺀 것으로 split하면 생기는 loss funtiondml reduction으로 이 값은 최대화할 대상이다.
2.3 shrinkage and Column Subsampling부턴 다음 시간에..
