[ML] Bayesian Network

바서기·2024년 3월 4일

ML

목록 보기

2/5

본 포스트는 서울대학교 데이터사이언스를 위한 머신러닝 및 딥러닝 2 이상학 교수님 수업과 수업 자료를 기반으로 작성하였습니다.
원래는 xgboost 논문의 내용을 이어 작성하려 했지만 오늘 수업을 듣고서 복습을 안하고선 따라갈 수 없겠다는 생각이 들어 작성하게 되었다.(그리고 이번에 듣는 수업 중 하나인 머신러닝 및 딥러닝 1에서 xgboost를 다루기 때문에 그 때 포스트해도 괜찮을 거 같다는 생각도 함.)
이 수업을 줄여서 MLDL2라고 부를 것인데 중간고사까지는 ML을 다루고 기말고사 때 DL을 다루는데 확실히 대학원 강의라서 그런가 내용이 깊다.
일단 최대한 이해할 수 있는 데까지 포스팅을 작성해보겠다.

0. Intro.

모델링의 목표는 현실에 존재하는 확률분포를 잘 나타내는 확률 모델을 만드는 것이다. 그 중에서 Bayesian Network(줄여서 BN)은 graph로 이 확률분포를 더 쉽게 표현하고자 만들어진 것인데 크게 Representation, D-seperation for reading conditional Independence, Inference 순으로 포스트를 작성하겠다.
확률이나 그래프의 전반적인 개념은 모두 안다고 가정
그래도 사용하는 개념을 쭉 나열해보면(대문자는 확률변수, 볼드체는 집합, 소문자는 값이 주어진 확률변수(=fixed)를 의미)
- random variables
- joint and marginal distributions
- conditional probability

P(X\mid Y) = \frac{P(X,Y)}{P(Y)}

- product rule

P(X,Y) = P(X\mid Y)P(Y)

- chain rule(any order)

P(X_1, X_2,...,X_n) = P(X_1)P(X_2\mid X_1)P(X_3\mid X_2, X_1)... \\ =\prod_{i=1}^nP(X_i\mid X_1,...,X_{i-1})

- independence

P(x,y) = P(x)P(y)\space (for \space all\space x\space and\space y) \\\space \\ then,\space X \perp\!\!\!\perp Y \\\space \\ P(x\mid y) = P(x)\space (for\space all\space x\space and\space y\space with\space P(y)>0)

- conditional independence (X is conditional independent of Y given Z)

P(x,y\mid z) = P(x\mid z)P(y\mid z) \\ P(x\mid y,z) = P(x\mid z) \\\space \\ then,\space X \perp\!\!\!\perp Y \mid Z

1. Representation

1.1 Bayesian Network 개요

BN은 domain의 확률 모델을 그래프를 통해 효율적으로 인코딩한 것이다.
확률 모델에는 다양한 변수들이 사용되는데 우리가 궁극적으로 알고 싶은 것인 이 변수들 간의 joint distribution이다.
그러나, full joint distribution(한 변수를 설명하는데 모든 변수들을 고려하는 것) table을 우리의 model로 사용하면 두 가지 문제점이 생기는데
1. 변수의 개수가 많다면, joint는 너무 커져서 설명력이 부족하게 된다.(overfitting의 우려도 있고 의미없는 변수들이 인과관계처럼 보일 수 있음.)
2. 주어진 시간내에 계산이 불가능할 수 있다.
따라서 bayesian network는 이러한 문제점을 sample, local distributions(conditional probabilities)을 통해 해결하려 한다. 즉 간단하게 이야기하면, locally(directly)하게 연관이 있는 변수들만 고려한다는 것. 그래서 이러한 local한 정보들로 global한 전체를 표현하는 것이 BN의 목표인 것이다.

1.2 Graphical Model Notation

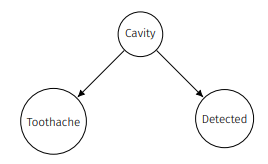
이번엔 graph의 각 요소가 BN에서 무엇을 의미하는지 알아보자.
- Nodes(vertices): variables
- Arces(edges): interactions(direct influence를 의미하고 연결 되어있지 않은 것들은 '주로' conditional independence를 의미) -> '주로'라는 단어의 의미는 뒤에서 알게될 것임...
- Arrows는 direct causation(인과관계)로 해석(실제로는 거의 그럴일 없긴 함.)

1.3 Semantics of Bayesian Network

이제 Bayesian Network에 대해 한 단계 더 다가가 BN의 구성을 살펴보면 BN은 Topology(topology는 위상해석을 의미하는데 BN에선 특히 DAG(directed acyclic graph), 유향 비순환 그래프를 의미)와 Conditional Distributions으로 이루어져 있다.

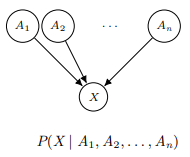
각 node에 conditional distribution이 존재하고 given에 주어지는 것들은 parent's values여서 위 노드의 conditional distribution을 간단한 식으로 표현하면 다음과 같다.

P(X\mid \mathbf{Pa}_x)

1.1에서 소개한 BN의 목표가 local한 정보로 global을 표현하는 것이라 했는데 이 목표를 어떻게 달성하냐면 conditional independences를 가정하기 때문이다. 식으로 보이면 chain rule에 의해

P(x_1, x_2,...,x_p)=\prod_{i=1}^pP(x_i\mid x_1,...,x_{i-1})

이고 conditional independences를 가정하면

P(x_1, x_2,...,x_p)=\prod_{i=1}^pP(x_i\mid \mathbf{pa}_{x_i})

로 볼 수 있다.
이는 local Markov Property로 해석할 수 있는데 Markov Property의 핵심은 현재에 영향을 주는 요인은 바로 이전의 결과들 뿐인 것이니 local을 붙여 현재 node에 영향을 주는 것은 이 node를 가리키는 parents node라는 점에서 local Markov Property로 보는 것이다.
BN은 계산을 간단해 할 수 있다는 점에서 유용해보이지만 우리가 까먹으면 안되는 것이 가정인 conditional independences이다.(실제 생활에선 쉽지만은 않은..) 이 가정으로 inference를 subsationally하게 simplify했기 때문에 초기에 graph를 잘 설정하는 것도 중요하다.

1.4 Causality

BN이 실제로 causal patterns(인과 관계)를 잘 반영한다면 간단해지고 생각하기 편하고 모델링하기 쉽다는 장점이 있지만 correlation만을 반영할 수도 있음.(correlation과 causation은 엄연히 다른 용어임.) 따라서 arrow들이 causality를 항상 반영한다고 보기 힘들고, conditional indepedence는 확실히 반영한다고 볼 수 있음.

1.5 Size of Bayesian Network

p개의 binary variables가 있다 하자. 이 때 joint distribution의 크기는 $2^p-1$ (마지막은 합이 1인 것으로 판단)라고 할 수 있다. 여기에 BN이 도입되어 p개의 node와 k개의 parents를 갖고 있다면 $O(p\cdot 2^k)$ 이다.(왜 이런지 생각해보면 p개 각각의 node에서 k개보다 더 많은 부모를 가질 수 없고 상수항을 무시하면 쉽게 유추할 수 있음.) 추가로 k는 p-1을 넘을 수 없으니 크기가 항상 작다 할 수 있고 실제로 k가 p-1인 fully connected일 확률은 작기 때문에 무조건 크기 측면에선 이득이다.
또한 뒤에서 얘기할 다른 장점으론 쉽게 도출하는 local CPTs(CPT: conditional probabilites table)이 있기 때문에 query에 대해 더 빠른 답변을 할 수 있다.

2. D-separation for Reading Conditional Independence

2.1 D-separation: Motivation

위 그림에서 $P(x,y,z,w)$ 를 구하려면 $P(x)P(y\mid x)P(z\mid y,x)P(w\mid z,y,x)$ 이고 conditional independence를 가정하면 $P(x)P(y\mid x)P(z\mid y)P(w\mid z)$ 라 할 수 있다.
local Markov Property에 의해 이전 부모 노드의 정보가 주어지면 다른 노드와는 독립인 것인데 한 단계 더 나아가 Y가 주어졌을 때 X와 W가 독립인지를 생각해보자.
결론부터 말하면 Y가 주어졌을 때 X와 W 역시 독립인데 수식으로 보이면 다음과 같다.

P(W,X\mid Y)=\frac{\sum_zP(W,Z,Y,X)}{P(Y)} = \frac{\sum_zP(X,Y)P(Z\mid Y,X)P(W\mid Z,Y,X)}{P(Y)} \\\space \\ =\frac{\sum_zP(X,Y)P(Z\mid Y)P(W\mid Z,Y)}{P(Y)} \\\space \\ =\frac{P(X,Y)\sum_zP(W,Z\mid Y)}{P(Y)} = P(X\mid Y)P(W\mid Y) \\\space \\ \therefore W \perp\!\!\!\perp X\mid Y

여기서 떠올릴 수 있는 부분이 conditional independence가 지켜지는 path가 연결될 수 있어보이는 것이다. 이것에 대해 얘기하기 전에 간단한 chain들을 봐보자.

2.2 Simple Cases

2.2.1 Chains

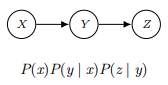
이 상황에선 X와 Z가 독립이라 볼 수 없다. 예시를 들어보면

P(y=1\mid x=1)=0.9, P(y=1\mid x=0)=0.1 \\ P(z=1\mid y=1)=0.9, P(z=1\mid y=0)=0.1

이런 상황에서 z가 1이면서 x도 1일 확률은 P(x=1)*(0.9*0.9+0.1*0.1)=P(x=1)*(0.82)인데 P(x=1)P(z=1)은 P(x=1)*(0.82)+(1-P(x=1))(0.1*0.9+0.9*0.1)으로 두 값이 같지 않다.
하지만 Y의 값이 주어진 경우 X와 Z는 독립이 되는데

P(z\mid x,y)=\frac{P(x,y,z)}{P(x,y)} \\\space \\ =\frac{P(x)P(y\mid x)P(z\mid y)}{P(x)P(y\mid x)} = P(z\mid y)

이기 때문이다.
이를 우리에게 주어진 'evidence'가 'influence'를 'block'했다고 표현하기도 한다.

2.2.2 Forks

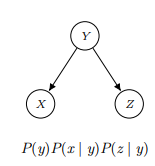
마찬가지로 이 상황에서도 evidence가 없다면 X와 Z가 독립이라고 보장할 수 없지만 y가 주어진다면

P(z\mid x,y)=\frac{P(x,y,z)}{P(x,y)} \\\space \\ =\frac{P(y)P(x\mid y)P(z\mid y)}{P(y)P(x\mid y)} = P(z\mid y)

이와 같은 식에 의해 독립을 보장할 수 있다.(chains와 forks의 차이는 P(x,y,z)를 구하는 식이 미묘하게 다르다.)

2.2.3 Collider

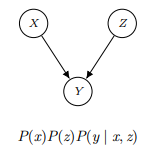
반면 collider같은 경우 위 두 cases와 다른데

P(x,z) = \sum_yP(x,y,z) \\\space \\ =\sum_yP(y\mid x,z)P(x)P(z) \\\space \\ =P(x)P(z)

이기 때문이다. 즉, collider의 형태는 evidence가 주어지지 않아도 독립인 것이다. 오히려 y가 주어진 경우

P(y=1\mid x=1, z=1)=0.6, P(y=1\mid x=1, z=0)=0.1 \\ P(y=1\mid x=0, z=1)=0.2, P(y=1\mid x=0, z=0)=0.1

y가 1일 때 x가 1이면서 z가 1일 확률은 0.6/(0.6+0.1+0.2+0.1)=0.6이지만 y가 1일 때 x가 1일 확률은 0.7/(0.6+0.1+0.2+0.1)=0.7이고 y가 1일 때 z가 1일 확률은 0.8/(0.6+0.1+0.2+0.1)=0.8이어서 $P(z,x\mid y) \neq P(z\mid x)P(z\mid y)$ 이므로 independent하지 않는다.

2.2.4 Active/Inactive Triplets

이렇게 세 개의 변수를 나타내는 path들을 active/inactive로 구분할 수 있는데 active(=open)의 경우
- A->B->C에서 B에 조건이 없는 경우
- Common cause B in A<-B->C인데 B가 주어지지 않은 경우
- Common effect B in A->B<-C인데 B가 주어지거나 B의 자손이 주어진 경우
들이 해당한다. 이를 그림으로 나타내면 다음과 같다.

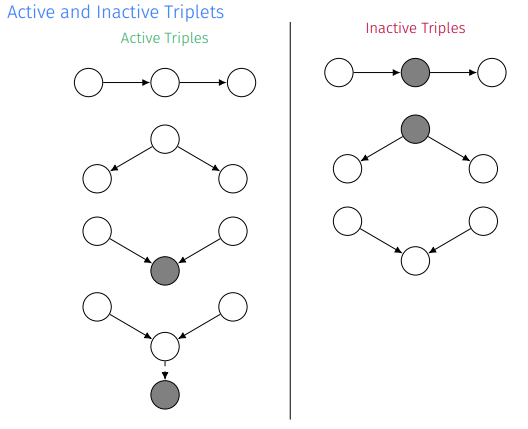
여기서 추측할 만한 intuition이 만약에 두 nodes에 여러 개의 path가 있고 그 중에 하나라도 active한 것이 있다면 어쨌거나 노드간 상호작용해야 하는 부분이 있기 때문에 independent하지 않을 것이라고 생각할 수 있다. 여기서 파생된것이 2.3 d-separation이다.
+ 위 1.2에서 연결 되있지 않은 노드들은 주로 conditional independence 하다에서 '주로'가 들어가는 이유가 위 active한 경우들 때문

2.3 D-separation

X와 Y가 d-separated by Z라는 것은 given Z에 대해 X와 Y 사이의 모든 path가 inactive함을 의미한다.
하지만 주의할 것이 d-separation이 아니라해서 항상 dependence인 것은 아닌 것인데 충분히 conditional independences가 생길 수 있기 때문이다.(fork와 collider로 이루어진 graph를 떠올리면 된다.)

2.4 Topology Limits Distribution

2.2.4에서 보다시피 topology에 따라 변수들의 관계가 결정되기 때문에 해당하는 topology가 cover할 수 있는 distribution에 제한이 생긴다.
또한 여기서 cost와 cover할 수 있는 distribution의 범위에 대한 trade-off가 존재하게 되는데 왜냐하면 edge가 많으면 cover할 수 있는 범위가 증가하기 때문이다.(실제 분포가 연결해야하는 분포이면 edge를 연결해야지 cover할 수 있지만 실제 분포가 연결하지 않아도 되는 분포이면 edge를 연결해도, 연결하지 않아도 cover할 수 있기 때문이다.)
즉, 우리가 graph를 설정할 때 실제 분포보다는 많이 edge를 만들게 될 것이기 때문에 우리가 생각한 것보다 더 많은 indepence가 있을 수도 있고 edge가 존재한다는 것은 그만큼 computation cost가 증가되기 때문에 trade-off가 존재하는 것이다.

2.5 중간 Summary

1. Represenation과 2. D-separation for Reading Conditional Independence에서 말한 내용을 정리해보면
1. Bayesian networks는 joint distributions에 conditional independences를 사용하여 compact하게 encoding한 것이다.
2. BN graph structure을 보면 node의 distributions 간의 독립성을 판단할 수 있다.
3. D-separation은 그래프만으로 엄밀한 conditional independece guarantees를 제공한다.
4. BN's joint distrubution은 아마 추가적인 indepence를 가질 수 있고 이를 발견하기 위해선 specific distribution을 알아보아야 한다.

3. Inference

Inference는 단어 그대로 추론을 의미해 우리가 원하는 joint probability distribution을 계산하는 것이다. 따라서, Posterior Probability(사후 확률)을 계산할 수도 있고 Most likely explanation(변수가 가질 값 중 확률이 가장 높은 것)을 구할 수도 있다.(둘을 구하는 과정은 크게 다르지 않다. 사후 확률을 알고 그 확률 중 가장 높은 값을 고를테니까) 예를들어,

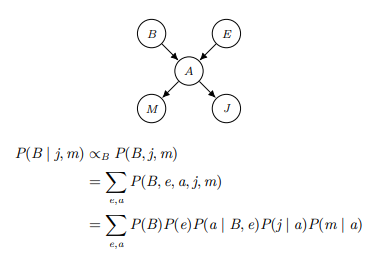
위와 같이 그래프가 생겼을 때 P(B | j, m) = P(B, j, m)/P(j, m)인데 j,m은 주어진 값으로 분모는 상수여서 아래 식의 비례관계가 성립한다. 이렇게 graph가 구성된 경우 모든 변수를 고려할 때보다 inference가 간단해 진다.

3.1 Inference by Enumeration

우리는 변수들을 evidence variables $E_1...E_k$ 와 query variables $\mathbf{Q}$ , 그리고 나머지들 hidden variables $\mathbf{H}$ 로 볼 수 있다.
우리가 원하는 것은 $P(\mathbf{Q}\mid e_1,...,e_k)$ 인데 이를 구하는 가장 간단하면서 정확한 방법을 소개하면 다음과 같다.
Step 1. evidence와 관련된 항들을 고른다.

P(\mathbf{Q,H,e})

Step 2. hidden variables에 대해 위 확률들을 더해 H를 소거한다.

P(\mathbf{Q,e}) = \sum_{\mathbf{h}}P(\mathbf{Q,H,e})

Step3. Normalize

P(\mathbf{Q}\mid \mathbf{e})=\frac{1}{Z}P(\mathbf{Q,e})

where $Z=\sum_{\mathbf{q}}P(\mathbf{q,e})$

이를 간단한 그래프에 적용하면 식이 위와 같이 나오는데 computation cost를 줄이는 방법인 variable elimination 아이디어가 나온다.

3.2 Variable Elimination

Variable elimination은 엄청 새로운 방법은 아니고 inference by enumeration의 식에서 시그마의 위치를 바꿔준것이다. 위 RTL 그래프에서 계산식에 적용하면

이렇게 r에 대한 시그마가 안쪽으로 들어가 r을 소거해버린다.
간단하게 예를 들어 몇 번의 계산이 줄어드는 지 보기 위해 r과 t가 10개씩 있다고 하자.(엄밀하진 않고 정성적으로)
이 때, inference by enumeration은 300회의 x와 100회의 +연산을 하게 되고 variable elimination은 t하나당 10회의 x와 10회의 +연산을 해 총 100회의 x와 100회의 +연산을 하게 된다.
정리하자면, variable elimination은 evidence와 local CPTs로 inital factors를 설정하고 hidden variables이 존재하는 경우 이 중 하나의 변수에 대해 이 변수를 언급하는 모든 factors를 join하고 sum에 제거해준다. 그다음 남은 facotrs를 join해주고 normalize하면 된다.
예시를 들어보면

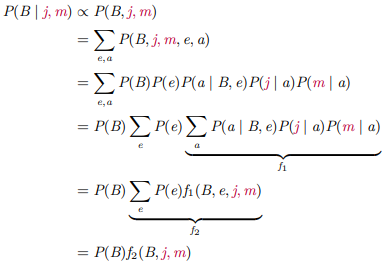
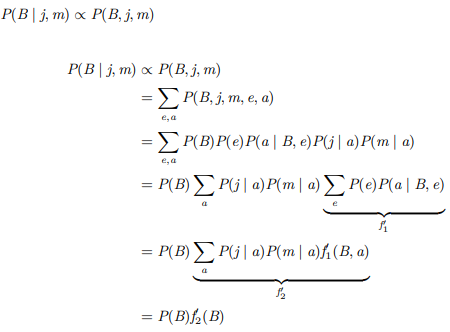
이렇게 되는데 같은 evidence 및 query variables더라도 hidden variable을 선정하는 순서에 따라 식이 달라지면 computation complexity도 달라진다.
다음과 같은 예에서도

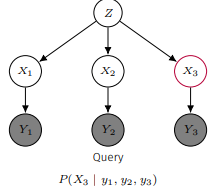
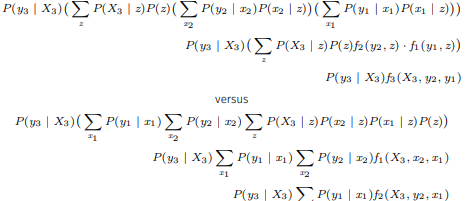
이렇게 순서가 달라질 수 있다.
하지만, 아쉽게도 최적의 순서를 구하는 방법은 알려져있지 않고 NP-hard에 해당한다. 최악의 경우 무려 BN의 크기의 지수함수 만큼의 시간이 걸린다.
3.1에서 소개한 inference by enumeration과 3.2에서 소개한 variable elimination은 모두 exact inference에 속한다.(이외에 Juntion Tree algorithm이 있지만 여기선 다루지 않겠다.) 이 방법을 쓰기 위한 필수 전제 조건이 probabilistic model을 알고 있어야 하는데 우리는 현실 세계의 분포를 정확하게 알고 있지 못한다. 따라서 대안으로 approximate inference이 알려져있는데 이에 대해 3.3에서부터 알아보자.

3.3 Sampling in Bayesian Networks

approximate infernce에도 여러 방법들이 있지만 이 포스트에선 sampling을 활용하는 방법(Monte Carlo 방법이라고도 하는데 정의는 무작위 샘플링을 이용하여 근사적 해를 구하는 계산 알고리즘이다.)만 다루겠다. sampling은 전체 모집단의 분포를 추측하기 위해 표본을 뽑는 과정을 의미하는데 sampling에도 여러 방법이 있어 각 방법의 장단점을 알아보자.

3.3.1 Prior Sampling

Prior sampling은 부모 노드가 없는 노드부터 시작해 각각의 조건부 확률을 계산하면 된다. 따라서 pseudo code가

로 매우 간단한 편인데 단점은 확률이 낮은 이벤트의 경우 충분한 수의 샘플을 생성하기 위해 많은 반복이 필요할 수 있고 증거 변수가 주어진 조건부 샘플링에서는 직접적으로 사용하기 어렵다.

3.3.2 Rejection Sampling

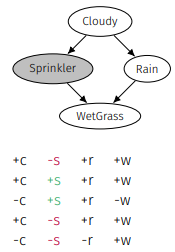
Rejection Sampling은 C outcomes에서 원하지 않은 결과들을 제거하는 방식이다. 위 상황에서 P(C|+s)를 구한다면 빨간색의 경우들을 모두 제거한다. Prior Sampling이 못하던 증거 변수가 주어진 조건부 샘플링이 가능해진다.

3.3.3 Likelihood Weighting

Rejection Sampling의 문제점은 많은 수의 samples을 버리게 될 수 있다는 것이고 샘플을 다 뽑고나서 이 샘플을 쓸지 말지 결정하기 때문에(조건은 이미 결정되어 있지만) 상당히 비효율적이다.
따라서 해결책으로 제안된 likelihood weighting은 evidence variables를 고정하고 나머지 변수들에대해 sampling을 진행한다. 이를 그대로 반영하면 당연히 생기는 문제점이 샘플링된 분포가 실제 조건부 확률 분포를 정확히 반영하지 못한다는 것이고 따라서 evidence의 부모 변수들의 조건부 확률에 따라 가중치를 부여한다.

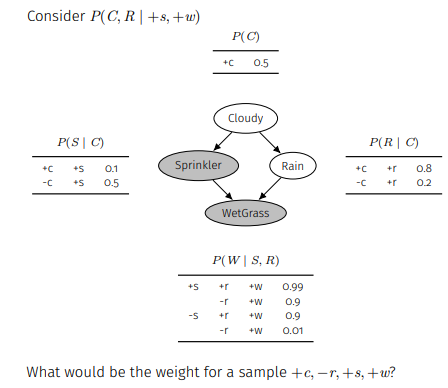
위 상황에서 부여되는 샘플의 가중치는 $P(+s\mid+c)\cdot P(+w\mid+s, -r)=0.1\cdot 0.9=0.09$ 가 되는 것이다.
pseudo code는 다음과 같고

이 아이디어가 왜 작동하는지 알아보면

위처럼 가중치를 부여하고 evidence를 고정시킨 sampling에 곱해주면 우리가 궁극적으로 구하고 싶어한 $P(z|e)$ 에 비례한 $P(z,e)$ 를 구할 수 있기 때문이다.
이처럼 likelihood weighting은 샘플링 과정에서 evidence를 고려하는 방법이긴 하지만 완벽한 해결책은 아니다. 왜냐하면 evidence가 evidence보다 아래쪽에 위치한 변수들에게는 영향을 미치지만 그보다 위에 있는 C같은 변수들에게는 영향을 미치지 않기 때문이다.(하지만 여기선 evidence를 고정시키기 때문에 모든 변수에 영향을 끼치게 된다.)

3.3.4 Gibbs Sampling

Likelihood weighting의 문제점을 해결하기 위해선 sampling하는 과정에서 evidence를 고려해야 했고 이를 반영한 것이 Gibbs sampling이다.
Gibbs sampling은 Markov Chain Monte Carlo(MCMC) methods 중 Metropolis-hastings의 special case로 충분히 많은 반복을 통해 마르코프 체인이 정상상태(sationary distribution)에 도달한 query distribution P(Q|e)에서 작동한다.
방법을 살펴보면

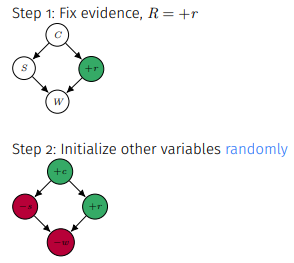
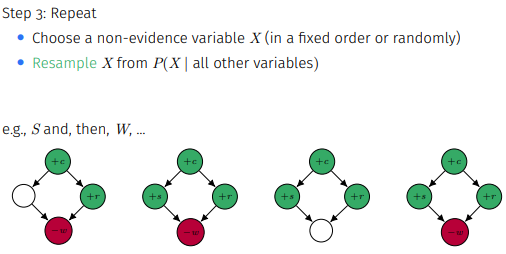
Evidence는 고정하고 나머지 변수를 하나씩 계속 수정하면서 마르코프 체인이 정상상태에 도달할 때까지 진행해 우리가 원하는 query variable의 확률 분포를 얻는다.
Likelihood weighting은 evidence의 위쪽 variables의 확률분포는 고려하지 못해 가중치가 매우 작게 나오기도 하는데 Gibbs sampling은 이를 보안해준다.

3.4 3절 Summary

- Enumeration과 Variable Elimination으로 Exact Inference를 할 수 있다.
- Samplig(prior, rejection, likelihood weighting, Gibbs)로 approximatie inferene를 할 수 있다.
- Gibbs sampling은 sampling하는 과정에서 모든 변수에 evidence를 고려할 수 있어 가장 이상적이다.

4. 마무리 및 느낀점

마무리는 두서 없이 feel 가는데로 써보면 오늘 수업은 ML의 근간이 되는 Bayesian Network에 대해 알아보았다. 실제 세계의 확률 분포를 이해하기 위해 그래프로 접근하였다는 간단한 내용부터 실제 세계의 확률 분포를 추론하기 위해 어떻게 sampling 해야하는지까지 꽤나 많은 내용을 알게 된 것 같다. 교수님께서 중간에 skip하시는 부분이 있어 GPT와 여러 자료들의 도움을 받았지만 일단 이번 차시는 모든 내용이 이해된 것 같아 뿌듯하다.(이런 내용들을 하니 머신러닝이랑 진대하는 느낌..)개강 첫 날부터 전산실에 이렇게 오래있을 줄 몰랐는데 허허.. 왠지 앞으로 전산실에 있을 일이 많을 것 같다. 아무튼 이제 집에 가야지 : )

바서기

인생 법칙 1. 기준 낮추기 않기 2. 일단 해보기 3. 긍정 마인드