Week1 : Descriptive Statistics and Visualizing Information
Introduction to Statistics 이름의 강의를 기반으로 내용을 이해하여 정리하였습니다. 첨부 이미지에 대한 저작권은 코세라에 있습니다.
Pie Chart & Dot Plot
데이터를 그래픽으로 표현하여 요약하는 것은 중요하다. 이런 정보를 정리하여 소통하는 방법중에 Pie chart, Dot plot이 있다.
질적 (qualitative) 데이터 (e.g., colors, car types)의 경우 pie chart나 dot plot으로 나타낼 수 있다.
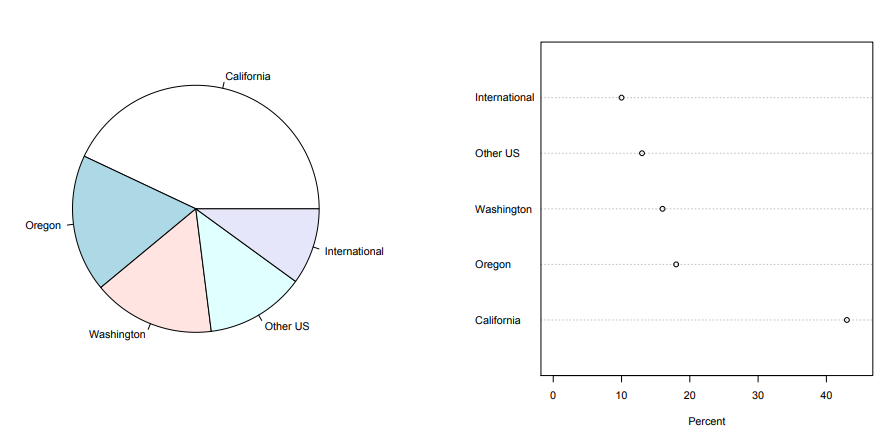
- 둘 다, 질적인 데이터를 표현하기 유리하지만 dot plot쪽이 frequencies를 표현하기에는 더 유리하다. 즉, 왼쪽 파이의 경우 Other US와 International의 portion을 비교하기 어렵지만, 오른쪽 plot의 경우 점의 위치로 쉽게 확인할 수 있다.
- Pie chat의 경우 대신, 한 눈에 전체에서 얼만큼 차지하는지 확인하기는 훨씬 용이하다.
Quantitative 데이터의 경우 (i.e. numbers) bar graph로 나타내기에 편하다. 예를 들어 한 반의 학생들의 수를 표현한다고 하면 아래와같이 그려볼 수 있다.
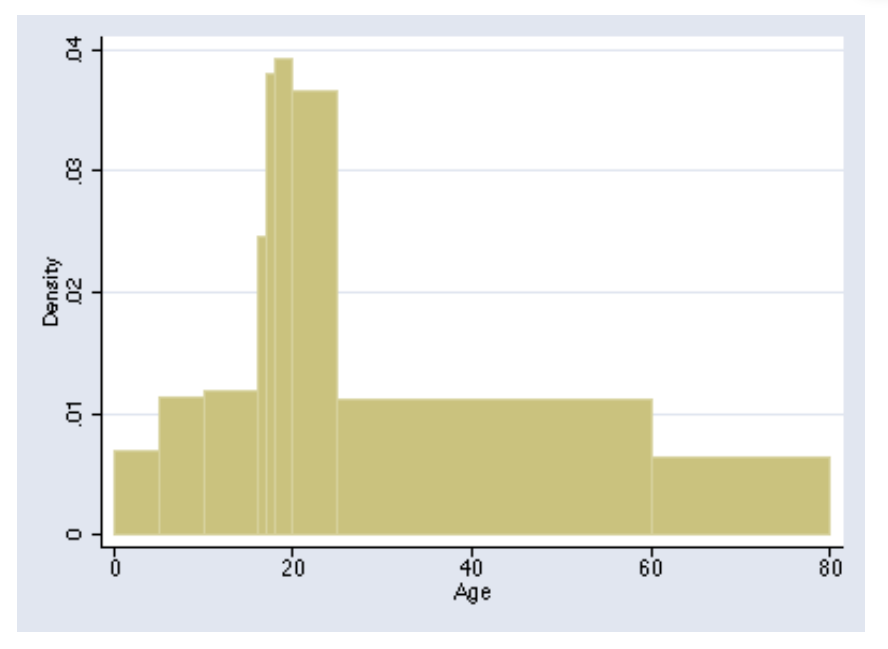
- Histogram으로도 표현해볼 수 있다. 이 때, 히스토그램은 서로 다른 widths를 가질 수 있는데, 중요한 요점은 각 block들이 표현하는 면적이 frequency와 비례한다는 것이다.
-
Histogram의 전체 면적은 100%와 동일하다. 특히, density scale를 표현하기 적절하며 ‘% per unit’ 을 표현하기 적절하다. 위 경우, ‘% per year’을 표현한 히스토그램이라고 읽을 수 있다.
-
Histogram을 통해서 두 가지 정보를 표현해볼 수 있다. 먼저 density이다. Bar의 높이가 의미하는 바는 얼마나 많은 주제가 한 unit에 있는지이다. 위 그림에서 19 연령은 4%를 차지한다는 것을 의미한다. 이에 비해 60-80 연령은 0.7% 차지한다는 것을 표현한다.
-
Percentage도 표현할 수 있다. 이 때, 면적(area)는 = 높이(height) x 너비(width)로 계산한다. 예를 들어, 60-80 연령은 14%라고 계산해볼 수 있는데 이는 20years * 0.7%로 계산해볼 수 있다.
Boxplot & Scatterplot
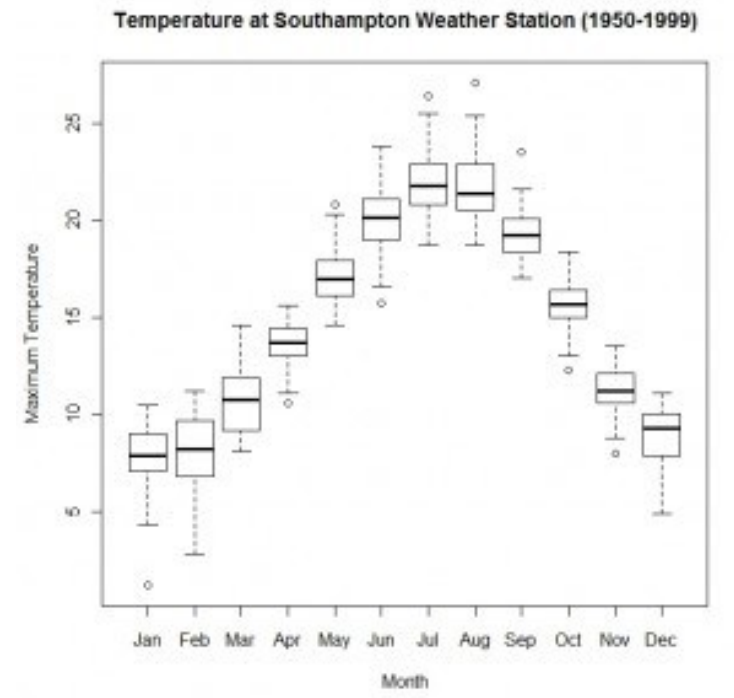
- Boxplot은 한번에 데이터의 통계를 잘 표현해줄 수 있는 그림이다. 즉, 최솟값-최댓값-중앙값 그리고 사분위수를 그림으로 표현한다.
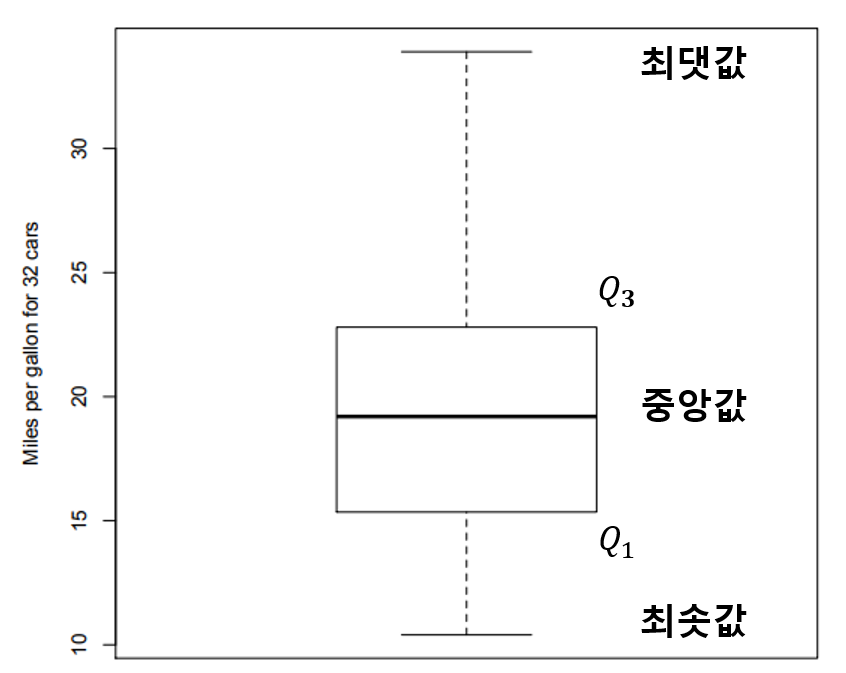
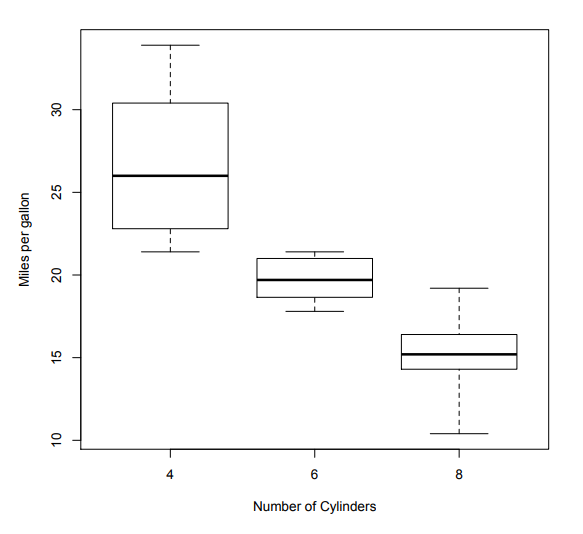
- Botplot은 histogram보다 한번에 전달할 수 있는 정보 양은 적지만, 아래와 같이 여러 데이터세트에 대해 비교하는데 매우 적합하다.
Scatterplot은 두 variables의 관계를 시각화하는데 사용한다.
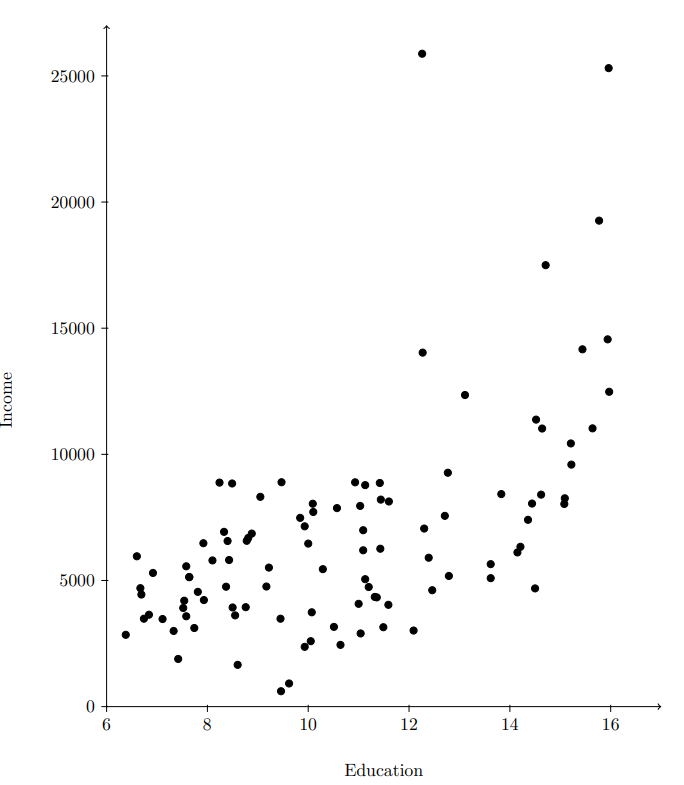
- 작은 박스들을 여러개 표현함으로써 맥락 정보를 표현할 수 있다.
Numerical summary measures
- Mean과 median은 언제 적절히 사용할까?
- 만약 데이터의 histogram이 대칭이라면 mean, median 동일하기 때문에 어떤 것을 사용하더라도 크게 상관은 없다. 하지만 데이터가 skewed 된 경우는 조금 다르다. 이 경우는, median을 사용하는 것이 유리하다.
- 이 경우, quartile 를 어디까지 볼 것인지에 따라서 mean과 median의 차이가 생긴다.
- Mean, std 모두 데이터를 요약하기 위해서 사용한다.
Mean :
Standard deviation : or
