문제
수열 S가 어떤 수 Sk를 기준으로 S1 < S2 < ... Sk-1 < Sk > Sk+1 > ... SN-1 > SN을 만족한다면, 그 수열을 바이토닉 수열이라고 한다.
예를 들어, {10, 20, 30, 25, 20}과 {10, 20, 30, 40}, {50, 40, 25, 10} 은 바이토닉 수열이지만, {1, 2, 3, 2, 1, 2, 3, 2, 1}과 {10, 20, 30, 40, 20, 30} 은 바이토닉 수열이 아니다.
수열 A가 주어졌을 때, 그 수열의 부분 수열 중 바이토닉 수열이면서 가장 긴 수열의 길이를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)
출력
첫째 줄에 수열 A의 부분 수열 중에서 가장 긴 바이토닉 수열의 길이를 출력한다.
풀이
[N][2] 크기의 2차원 dp 배열을 생성한다.
A[i]로 끝나는 증가하는 수열, A[i]로 끝나며 중간에 꺾이고 감소 중인 수열을 모두 구해야 한다.
2차원 dp 배열의 [i][0]번째 index에는 A[i]로 끝나며 가장 긴 증가하는 부분 수열의 길이를 저장한다. [i][1]번째 index에는 A[i]로 끝나며 중간에 꺾여서 감소하는 중인 부분 수열의 길이를 저장한다. i = 1부터 N-1 까지 반복하며 dp 배열을 채워준 다음 그 중 최댓값을 반환한다.
처음에는 [i][0]번째 index에 A[i]로 끝나며 바이토닉 수열이면서 가장 긴 수열의 길이를 저장하고, [i][1]번째 index에는 증가하는 중인지, 감소하는 중인지를 0과 1로 구분해서 저장했다. 그러나 다음과 같은 경우 문제가 발생한다.
예를 들어 {1, 5, 2, 1, 4, 3, 4, 5, 2, 1} 과 같은 수열이 있다고 가정하자. dp[0] = 1, dp[1] = 2, dp[2] = 3, dp[3] = 4, dp[4] = 3, dp[5] = 4가 저장될 것이다. dp[5]가 나타내고 있는 수열은 {1, 2, 4, 3}이 될 것이다. 이제 dp[6]을 탐색해보자. A[5]와 A[6]을 비교했을 때 A[6]이 더 크다. dp[5]에는 감소하고 있는 수열이 저장되어 있기 때문에 조건을 만족하지 못하고 dp[6]이 갱신되지 않는다. dp[6]에는 {1, 2, 3, 4} 부분 수열의 길이인 4가 저장되어야 한다. 그러려면 3이 있는 A[5]를 사용해야 하며, dp[5]에 {1, 2, 3}이 저장되어 있어야만 한다. 그러나, dp[5]를 탐색하는 시점에서는 {1, 2, 4, 3} 이 가장 긴 부분 수열이기 때문에 {1, 2, 3}이 저장되어 있는 dp 가 없게 된다. 따라서, 증가하고 있는 부분 수열과 감소하고 있는 부분 수열의 최장 길이를 따로 저장해서 각자 비교해야 한다.
dp 배열에는 다음과 같이 저장된다.
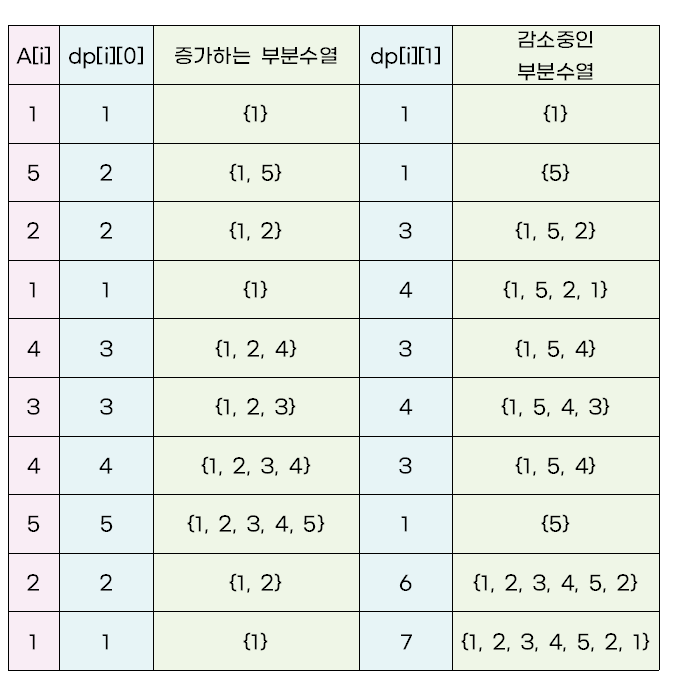
증가하는 부분 수열의 길이는 백준 11053번 문제와 같이 구할 수 있다.
- 현재 구하려고 하는 dp의 인덱스는 [4][0]라고 하자.
- A[4] 값인 4를 A[3] ~ A[0]까지 비교한다.
- A[3] (=1) < A[4] (=4) 이다. dp[3][0] (=1)에 1을 더한 값인 2를 dp[4][0]에 저장한다.
- A[2] (=2) < A[4] (=4) 이다. dp[2][0] (=2)에 1을 더한 값인 3을 dp[4][0]에 저장한다.
- A[1] (=5) > A[4] (=4) 이다. 5가 중간에 있게 되면 4로 끝나는 증가하는 부분 수열을 만들 수 없기 때문에 넘어간다.
- A[0] (=1) < A[4] (=4) 이다. dp[1][0] (=1)에 1을 더한 값인 2는 이미 dp[4][0]에 저장되어 있는 3보다 작기 때문에 넘어간다.
코드로 나타내면 다음과 같다.
for (int i = 1; i < N; i++) {
for (int j = i - 1; j >= 0; j--) {
if (A[j] < A[i]) {
dp[i][0] = Math.max(dp[i][0], dp[j][0] + 1);
}
}
}지금 탐색 중인 A[i]보다 A[j]의 값이 클 경우에만 A[i]로 끝나는 감소 중인 부분 수열을 만들 수 있다. 다음 세 가지를 비교한다.
- 현재 dp에 저장된 값
dp[i][1] - 증가하고 있는 dp[j][0]에 1을 더한 값
dp[j][0] + 1
dp[j][0]이 나타내는 수열이 {10, 20, 30, 40}이고 A[i]의 값이 30이라면 {10, 20, 30, 40, 30}으로 30으로 끝나는 감소 중인 부분 수열이 만들어진다. - 감소 중인 dp[j][1]에 1을 더한 값
dp[j][1] + 1
dp[j][1]이 나타내는 수열이 {10, 20, 30, 20}이고 A[i]의 값이 10이라면 {10, 20, 30, 20, 10}으로 10으로 끝나는 감소 중인 부분 수열이 만들어진다.
이 세 가지 경우 중 최댓값을 dp[i][1]에 저장한다.
코드로 나타내면 다음과 같다.
for (int i = 1; i < N; i++) {
for (int j = i - 1; j >= 0; j--) {
if (A[j] > A[i]) {
dp[i][1] = Math.max(dp[i][1], Math.max(dp[j][1] + 1, dp[j][0] + 1));
}
}
}dp 배열을 다 채웠다면 모든 값을 탐색해 최댓값을 찾아 반환하면 된다.
전체 코드는 다음과 같다.
전체 코드
import java.io.*;
import java.util.*;
class Main {
public static int[][] dp;
public static int[] A;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
A = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
A[i] = Integer.parseInt(st.nextToken());
}
bw.write(String.valueOf(dfs(N)));
bw.flush();
bw.close();
}
public static int dfs(int N) {
dp = new int[N][2];
for (int i = 0; i < N; i++) {
Arrays.fill(dp[i], 1);
}
for (int i = 1; i < N; i++) {
for (int j = i - 1; j >= 0; j--) {
if (A[j] < A[i]) {
dp[i][0] = Math.max(dp[i][0], dp[j][0] + 1);
}
if (A[j] > A[i]) {
dp[i][1] = Math.max(dp[i][1], Math.max(dp[j][1] + 1, dp[j][0] + 1));
}
}
}
int max = Integer.MIN_VALUE;
for (int i = 0; i < N; i++) {
if (max < dp[i][0]) max = dp[i][0];
if (max < dp[i][1]) max = dp[i][1];
}
return max;
}
}