[백준] 11053번 가장 긴 증가하는 부분 수열

문제

A = {10, 20, 10, 30, 20, 50} 이러한 수열이 주어졌을 때 가장 긴 증가하는 부분 수열을 구해라.
answer = {10, 20, 30, 50}
부분 집합이 아니라 부분 수열임.
수열의 최대 길이는 1000이다.

---

풀이1

바로 생각나는 방법은 특정 위치에서 앞의 원소들과 전부 비교하여 최대값을 계속 비교하며 갱신해주는 것이다.
그렇다면 사용할 방법은 2중for문, 값들을 기록해놓을 DP배열
나머지는 코드에서 설명하겠다.

전체코드1 (DP)

import sys
input = sys.stdin.readline

n = int(input())
numList = list(map(int, input().split()))
# 값을 기록해 놓을 DP배열
dp = [1 for _ in range(n)]

# i 위치의 원소와 i 보다 앞에 있는 원소들과 비교
for i in range(1, n):
    for j in range(i):
    	# 앞의 원소보다 클 때 dp[i]를 갱신
        if numList[i] > numList[j]:
            dp[i] = max(dp[i], dp[j] + 1)

print(max(dp))

풀이2

두번째 방법은 이분탐색을 이용하는 것이다.
여기서의 키포인트는 가장 긴 증가하는 부분 수열을 만들 수 있는 환경을 제공하는 것이다.
즉, 맨 앞 원소에서부터 LIS 배열에 넣고, 다음 원소부터 LIS의 맨 끝에 들어있는 수보다 작다면 더 작은것으로 교체하여 길게 만들 수 있게 해주고, 크다면 이어주는것이다.

예시를 통해 알아보자.
A = {7, 4, 3, 6, 5, 2, 1, 8, 9, 0} 일 때 이분탐색을 통해 LIS의 길이를 구해라.
lis = [7] 을 선언한다.
binarySearchLeft를 통하여 나온 인덱스를 위치로 원소들을 추가한다.

def binarySearchLeft(arr: list, target: int) -> int:
    left, right = 0, len(arr) - 1

    while left <= right:
        mid = (left + right) // 2

        if arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    
    return left

a = [7, 4, 3, 6, 5, 2, 1, 8, 9, 0]
lis = [7]

for i in range(1, len(a)):
    target = a[i]
    targetPos = binarySearchLeft(lis, target)

    # 위치와 길이가 같다면 뒤로 추가
    if targetPos == len(lis):
        lis.append(target)
    # 더 작은 원소로 교체
    else:
        lis[targetPos] = target
    
    print(f'target {target}의 위치는 {targetPos}번째 인덱스입니다.')
    print(f'{i}) lis = {lis}')
    print()

위의 코드를 실행하면 다음과 같다.

최종결과를 보면 lis = [0, 5, 8, 9]로 길이는 4이다.
즉, 이분탐색으로는 진짜 LIS는 얻을 수 없고 길이만 알 수 있다.
이유를 살펴보자.

실제 lis = [3, 5, 8, 9]이다. 9)의 경우만 살펴보자.
0이 3을 대체했다. 정확히 표현하면 0이 3의 위치를 대체한 것이다.
5의 앞에 0이 존재하고, 0은 3을 대체했다.
즉, 5의 앞에 5보다 작은 원소가 존재했다는 것이다. 때문에 정확한 LIS를 알 수 없지만 길이는 알 수 있는것이다.

그러면 정확한 LIS는 어떻게 알 수 있을까?
바로 각각의 원소들이 LIS 배열에 존재했던 인덱스를 기록해 놓으면 된다.

def binarySearchLeft(arr: list, target: int) -> int:
    left, right = 0, len(arr) - 1

    while left <= right:
        mid = (left + right) // 2

        if arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    
    return left

a = [7, 4, 3, 6, 5, 2, 1, 8, 9, 0]
lis = [7]
order = [0 for _ in range(len(a))]

for i in range(1, len(a)):
    target = a[i]
    targetPos = binarySearchLeft(lis, target)

    # 위치와 길이가 같다면 뒤로 추가
    if targetPos == len(lis):
        lis.append(target)
    # 더 작은 원소로 교체
    else:
        lis[targetPos] = target

    order[i] = targetPos
    
    print(f'target {target}의 위치는 {targetPos}번째 인덱스입니다.')
    print(f'{i})  lis  = {lis}')
    print(f'   order = {order}')
    print()

실행결과는 다음과 같다.

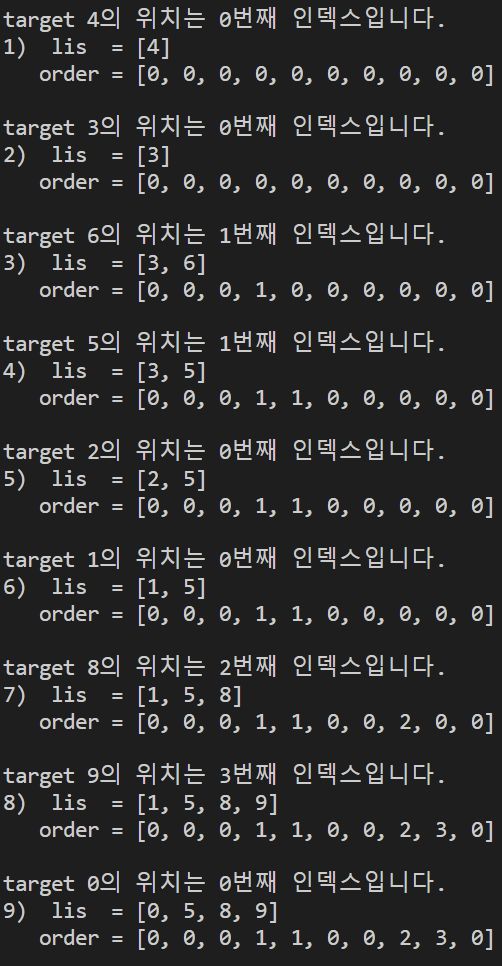
최종 order와 a = [7, 4, 3, 6, 5, 2, 1, 8, 9, 0]를 비교해보자.

a     = [7, 4, 3, 6, 5, 2, 1, 8, 9, 0]
order = [0, 0, 0, 1, 1, 0, 0, 2, 3, 0]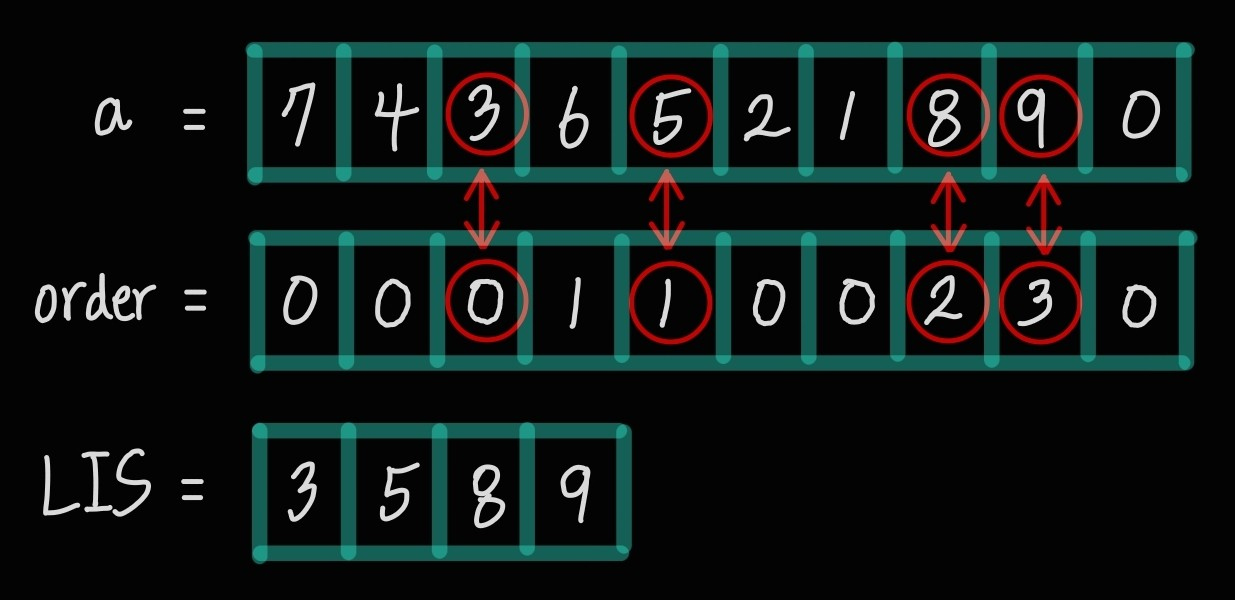

규칙이 보이는가? order를 역순으로 읽으면서 3, 2, 1, 0 순서를 채워넣으면 된다.

이제 LIS의 길이를 구하고, 실제 LIS가 무엇인지 구하는 최종코드를 살펴보자.

전체코드2 (이분탐색)

import sys
input = sys.stdin.readline

def binarySearchLeft(arr: list, target: int) -> int:
    left, right = 0, len(arr) - 1

    while left <= right:
        mid = (left + right) // 2

        if arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    
    return left

n = int(input())
a = list(map(int, input().split()))
lis = [a[0]]
order = [0 for _ in range(len(a))]

for i in range(1, len(a)):
    target = a[i]
    targetPos = binarySearchLeft(lis, target)

    # 위치와 길이가 같다면 뒤로 추가
    if targetPos == len(lis):
        lis.append(target)
    # 더 작은 원소로 교체
    else:
        lis[targetPos] = target

    order[i] = targetPos

answerLen = len(lis)
answerLIS = [0 for _ in range(answerLen)]
curPos = answerLen - 1

# 뒤에서부터 LIS를 만들어줌
for i, num in enumerate(order[::-1]):
    # 현재순서와 값이 같다면 기록
    if curPos == num:
        answerLIS[curPos] = a[(i + 1) * -1]
        # 다음순서
        curPos -= 1

print(answerLen)
print(*answerLIS)