[기초수학] Chapter01. 기초수학(등차수열, 등비수열, 계차수열, 피보나치수열, 팩토리얼, 군수열, 순열, 조합)

황성미·2023년 7월 18일
기초수학제로베이스제로베이스데이터스쿨제로베이스스쿨파이썬파이썬기초
0

제로베이스 데이터스쿨

목록 보기
10/58
post-thumbnail
post-custom-banner

✍🏻 17일 공부이야기.




등차수열

  • 등차수열 : 차이가 같은 수들의 나열
    sn=n(a1+an)/2s_n = n(a_1 + a_n) / 2

n번째 항까지의 합을 출력하는 프로그램을 완성해라

inputa1 = int(input('a1 입력 : '))
inputD = int(input('공차 입력 : '))
inputN = int(input("n 입력 : "))

valueN = 0 #n번쨰 항의 값
sumN = 0 #n번쨰 항까지의 합
n = 1

print("처음부터 끝까지 수열들을 더하는 방법")
while n <= inputN: #n번째 항까지
  if n == 1: #n이 1일 때는
    valueN = inputa1
    sumN += valueN #a1을 sumN에 더해주고
    print(f'{n}번째 항까지의 합 : {sumN}')
    n += 1
    continue
  #2번째 항부터 n번째 항까지는  
  valueN += inputD #공차를 더한 값들을
  sumN += valueN #계속 더해줌
  print(f"{n}번째 항까지의 합 : {sumN}")
  n += 1
print(f"{inputN}번째 항까지의 합 : {sumN}")


#등차수열 합 공식 : sn = n(a1 + an) / 2
print("등차수열 합 공식을 이용한 방법")
valueN = inputa1 + (inputN - 1)*inputD
sumN = inputN * (inputa1 + valueN) / 2
print(f"{inputN}번째 항까지의 합 : {int(sumN)}")

💻 출력
a1 입력 : 5
공차 입력 : 4
n 입력 : 5
처음부터 끝까지 수열들을 더하는 방법
1번째 항까지의 합 : 5
2번째 항까지의 합 : 14
3번째 항까지의 합 : 27
4번째 항까지의 합 : 44
5번째 항까지의 합 : 65
5번째 항까지의 합 : 65
등차수열 합 공식을 이용한 방법
5번째 항까지의 합 : 65


등비수열

  • 등비수열 : 연속된 두 항의 비가 일정한 수열
    an=a1∗rn−1a_n = a_1 * r^{n-1}
    sn=a1∗(1−(rn))/(1−r)s_n = a_1 * (1 - (r^n)) / (1 - r)

  • 등비중항 : 연속된 세 항에서의 가운데 항

n번째 항의 값을 출력하는 프로그램을 완성해라

inputa1 = int(input('a1 입력 : '))
inputR = int(input('공비 입력 : '))
inputN = int(input("n 입력 : "))

an = 0
n = 1
while n <= inputN:
  if n == 1:
    an = inputa1
    print(f'{n}번째 항의 값 : {an}')
    n += 1
    continue
  an *= inputR
  print(f'{n}번째 항의 값 : {an}')
  n += 1
print(f'{inputN}번째 항의 값 : {an}')

##an = a1 * r^(n-1)을 이용하는 방법
#an = inputa1 * (inputR ** (inputN -1))

💻 출력
a1 입력 : 2
공비 입력 : 2
n 입력 : 7
1번째 항의 값 : 2
2번째 항의 값 : 4
3번째 항의 값 : 8
4번째 항의 값 : 16
5번째 항의 값 : 32
6번째 항의 값 : 64
7번째 항의 값 : 128
7번째 항의 값 : 128

n번째 항까지의 합을 출력하는 프로그램을 완성해라

inputa1 = int(input('a1 입력 : '))
inputR = int(input('공비 입력 : '))
inputN = int(input("n 입력 : "))

valueN = 0
sumN = 0
n = 1

print("처음부터 끝까지 수열들을 더하는 방법")
while n <= inputN:
  if n == 1:
    valueN = inputa1
    sumN += valueN
    print(f'{n}번째 항까지의 합 : {sumN}')
    n += 1
    continue
  valueN *= inputR
  sumN += valueN
  print(f"{n}번째 항까지의 합 : {sumN}")
  n += 1
print(f"{inputN}번째 항까지의 합 : {sumN}")


#등비수열 합 공식 : sn = a1 * (1 - (r^n)) / (1 - r)
print("등비수열 합 공식을 이용한 방법")
sumN = inputa1 * (1 - (inputR ** inputN)) / (1 - inputR)
print(f"{inputN}번째 항까지의 합 : {int(sumN)}")

💻 출력
a1 입력 : 5
공비 입력 : 3
n 입력 : 7
처음부터 끝까지 수열들을 더하는 방법
1번째 항까지의 합 : 5
2번째 항까지의 합 : 20
3번째 항까지의 합 : 65
4번째 항까지의 합 : 200
5번째 항까지의 합 : 605
6번째 항까지의 합 : 1820
7번째 항까지의 합 : 5465
7번째 항까지의 합 : 5465
등비수열 합 공식을 이용한 방법
7번째 항까지의 합 : 5465


계차수열

  • 계차수열 : 어떤 수열의 인접하는 두 항의 차로 이루어진 또 다른 수열
    ana_n = {0 , 3 , 8 , 15 , 24 , 35 , 48 ...}
    bnb_n = {3 , 5 , 7 , 9 , 13 , 15 ...}
    👀 {bnb_n}은 {ana_n}의 계차수열이다.
    이때,
    ∑n=1n−1bn=an−a1\displaystyle\sum_{n=1}^{n-1}{b_n} = a_n - a_1성질과 - (1)
    bnb_n 은 공차가 2인 등차수열이므로 기존 등차수열 공식인
    bn=b1+(n−1)∗db_n = b_1 + (n - 1) * d 를 통해 구한 bnb_n의 일반식을
    sn−1=n(b1+bn−1)/2s_{n-1} = n(b_1 + b_{n-1}) / 2 에 대입하여 구한 값이랑 같다고 두고 -(2)
    ana_n 을 구하면 아래와 같이 일반식을 구할 수 있다.
    bnb_n 의 b1=3,d=2b_1 = 3 , d = 2이므로 bn=2n+1b_n = 2n + 1 이다.
    (1)과 (2)를 이용하여
    sn−1=(n−1)(3+(2(n−1)+1))/2=an−0\begin{aligned} s_{n-1} = (n - 1)(3 + (2(n-1) + 1)) / 2 = a_n - 0 \end{aligned}
    an=n2−1a_n = n^2 -1
    라고 {ana_n}을 구할 수 있다.

파이썬으로 구해보면 아래와 같다. 

# an = {3, 7, 13, 21, 31, 43, 57}
# bn =   4, 6,  8, 10, 12,  14

inputAN1 = int(input("a1 입력 : "))
inputAN = int(input("n 입력 : "))

inputBN1 = int(input("b1 입력 : "))
inputBD = int(input("bn 공차 입력 : "))

valueAN = 0
valueBN = 0

n = 1
while n <= inputAN:
  if n == 1:
    valueAN = inputAN1
    valueBN = inputBN1
    print(f'an의 {n}번째 항의 값 : {valueAN}')
    print(f'bn의 {n}번째 항의 값 : {valueBN}')
    n += 1
    continue
  valueAN += valueBN
  valueBN += inputBD
  print(f'an의 {n}번째 항의 값 : {valueAN}')
  print(f'bn의 {n}번째 항의 값 : {valueBN}')
  n += 1

print(f'an의 {inputAN}번째 항의 값 : {valueAN}')
print(f'bn의 {inputAN}번째 항의 값 : {valueBN}')

💻 출력
a1 입력 : 3
n 입력 : 7
b1 입력 : 4
bn 공차 입력 : 2
an의 1번째 항의 값 : 3
bn의 1번째 항의 값 : 4
an의 2번째 항의 값 : 7
bn의 2번째 항의 값 : 6
an의 3번째 항의 값 : 13
bn의 3번째 항의 값 : 8
an의 4번째 항의 값 : 21
bn의 4번째 항의 값 : 10
an의 5번째 항의 값 : 31
bn의 5번째 항의 값 : 12
an의 6번째 항의 값 : 43
bn의 6번째 항의 값 : 14
an의 7번째 항의 값 : 57
bn의 7번째 항의 값 : 16
an의 7번째 항의 값 : 57
bn의 7번째 항의 값 : 16

물론, 이 문제 또한 위에서 구한 것과 같이 일반항을 구해서 수식을 입력해줘도 구할 수 있다 :)


피보나치 수열

  • 피보나치 수열 : 세 번째 항이 두 번째 항과 첫 번째 항을 더한 합인 수열 an=an−2+an−1a_n = a_{n-2} + a_{n-1}
    (단, 첫째항과 둘째항은 모두 1이다)
    {1, 1, 2, 3, 5, 8, 13, ...}

피보나치 수를 계산하는 프로그램을 완성해라.

inputN = int(input('n 입력 : '))
valueN = 0 #n번째 항의 값
sumN = 0 #n번째 항까지의 합

valuePreN2 = 0
valuePreN1 = 0

n = 1
while n <= inputN:
  if n == 1 or n == 2: #첫번째 항과 두번째 항은 값이 1임
    valueN = 1
    valuePreN2 = valueN
    valuePreN1 = valueN
    sumN += valueN
    print(f'{n}번째 항의 값 : {valueN}')
    n += 1
    
  else:
    valueN = valuePreN2 + valuePreN1 #피보나치수열 특징
    valuePreN2 = valuePreN1
    valuePreN1 = valueN
    sumN += valueN
    print(f'{n}번째 항의 값 : {valueN}')
    n += 1

print(f'{inputN}번째 항의 값 : {valueN}')
print(f'{inputN}번째 항까지의 합 : {sumN}')

💻 출력
n 입력 : 5
1번째 항의 값 : 1
2번째 항의 값 : 1
3번째 항의 값 : 2
4번째 항의 값 : 3
5번째 항의 값 : 5
5번째 항의 값 : 5
5번째 항까지의 합 : 12


팩토리얼

  • 팩토리얼 : 1부터 양의 정수 n까지의 정수를 모두 곱한 것
inputN = int(input("n 입력 : "))

#반복문을 이용하는 방법(for문, while문)
result = 1
for n in range(1, inputN + 1):
  result *= n
print("for문을 이용하는 방법")
print(f'{inputN} 팩토리얼 : {result}')

result = 1
n = 1
while n <= inputN:
  result *= n
  n += 1
print("while문을 이용하는 방법")
print(f'{inputN} 팩토리얼 : {result}') 

#재귀함수를 이용하는 방법
def factorial(n):
  if n == 1:
    return 1
  return n * factorial(n-1)
print("재귀함수를 이용하는 방법")
print(f'{inputN} 팩토리얼 : {factorial(inputN)}')

##math 모듈을 사용하는 방법
#import math
#math.factorial(inputN)

💻 출력
n 입력 : 5
for문을 이용하는 방법
5 팩토리얼 : 120
while문을 이용하는 방법
5 팩토리얼 : 120
재귀함수를 이용하는 방법
5 팩토리얼 : 120


군수열

  • 군수열 : 여러 개의 항을 묶었을 때 규칙성을 가지는 수열
    1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1, 2, 3, 4, 5, ...
    (1), (1, 2), (1, 2, 3), (1, 2, 3, 4), ...
    각 군에 해당하는 항의 개수가 1개, 2개, 3개, 4개, .. 형태로 늘어난다!

다음 수열 {1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1, 2, 3, 4, 5, ...}의 n번째 항의 값을 출력하는 프로그램을 완성해라.

#1, 1, 2, 1, 2, 3, 1, 2, 3, 4, ...

inputN = int(input('n 입력 : '))

flag = True
n = 1
nCnt = 1 #n번째 항
searchN = 0 #n번째 항의 값

while flag:
  for i in range(1, n+1): #군
    print(f'{i} ', end = '')
    nCnt += 1
    
    if nCnt > inputN: #사용자가 원하는 n번째 항의 순서가 왔다면
      searchN = i #n번째 항의 값은 i가 된다.
      flag = False
      break
  print() #군이 바뀌면 줄바꿈을 해준다
  n += 1

print(f'{inputN}항 : {searchN}')

💻 출력
n 입력 : 17
1
1 2
1 2 3
1 2 3 4
1 2 3 4 5
1 2
17항 : 2

다음 수열 {1/1, 1/2, 2/1, 1/3, 2/2, 3/1, 1/4, 2/3, 3/2, 4/1, ...}의 n번째 항의 값을 출력하는 프로그램을 완성해라.

inputN = int(input('n 입력 : '))

flag = True
n = 1
nCnt = 1
searchNC = 0 #분자
searchNP = 0 #분모


while flag:
  for i in range(1, n+1):
    print(f'{i}/{(n - i + 1)} ',end = '')
    nCnt += 1
    if nCnt > inputN:
      searchNC = i
      searchNP = n - i + 1
      flag = False
      break
  print()
  n += 1
print(f"{inputN}항 : {searchNC}/{searchNP} ")

💻 출력
n 입력 : 9
1/1
1/2 2/1
1/3 2/2 3/1
1/4 2/3 3/2
9항 : 3/2


순열

  • 순열 : n개의 숫자들 중 순서를 고려하여 r개를 택하는 경우의 수
    n(n-1)(n-2)...(n-r+1) 단 0 < r <= n 으로 나타낼 수 있는데
    팩토리얼을 이용하면 n!(n−r)!n! \over (n-r)! 로 나타낼 수도 있다.
    이를 파이썬으로 코딩해보면 아래와 같다.
numN = int(input('numN 입력 : '))
numR = int(input('numR 입력 : '))
result = 1

#n(n-1)(n-2)...(n-r+1)을 이용한 방법
for n in range(numN, numN-numR, -1):
  print(f'n : {n}')
  result *= n
print(f'result = {result}')

#n! / (n-r)!를 이용한 방법
import math
print(f'result with factorial : {math.factorial(numN) / math.factorial(numN - numR)}')

💻 출력
numN 입력 : 7
numR 입력 : 5
n : 7
n : 6
n : 5
n : 4
n : 3
result = 2520
result with factorial : 2520.0


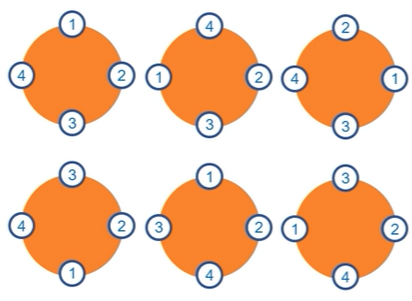
원순열

  • 원순열 : 시작과 끝의 구분이 없는 순열로서, (n-1)!로 계산됨.
n = int(input('n 입력 : '))
result = 1

for i in range(1, n):
  result *= i
print(f'result : {result}')

💻 출력
n 입력 : 4
result : 6


조합

  • 조합 : n개의 숫자들 중 순서를 고려하지 않고 r개를 택하는 경우의 수

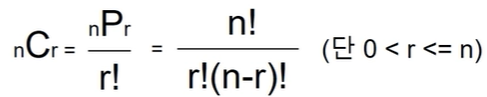
    위 공식을 파이썬을 이용해 나타내면 아래와 같다. 
numN = int(input("numN 입력 : "))
numR = int(input("numR 입력 : "))

resultP = 1
resultR = 1
resultC = 1

for n in range(numN, numN-numR, -1): #분자
  print(f'n1 : {n}')
  resultP *= n
print(f'resultP = {resultP}')

for n in range(numR, 0, -1): #분모
  print(f'n2 : {n}')
  resultR *= n
print(f'resultR = {resultR}')

resultC = int(resultP / resultR)
print(f'resultC = {resultC}')

💻 출력
numN 입력 : 8
numR 입력 : 3
n1 : 8
n1 : 7
n1 : 6
resultP = 336
n2 : 3
n2 : 2
n2 : 1
resultR = 6
resultC = 56


확률

  • 확률 : 모든 사건에서 특정 사건이 일어날 수 있는 경우의 수 (특정 사건이 일어날 경우의 수 / 모든 사건의 경우의 수)






오늘의 주저리

profile
황성미
데이터 분석가(가 되고픈) 황성미입니다!
이전 포스트

[기초수학] Chapter01. 기초수학(약수, 소수, 소인수분해, 최대공약수, 최소공배수, 수열)

다음 포스트

[기초수학] Chapter02. 기초수학 문제 풀이

post-custom-banner

4개의 댓글

comment-user-thumbnail
이태균
2023년 7월 18일

너무 좋은 글이네요. 공유해주셔서 감사합니다.

1개의 답글
comment-user-thumbnail
happy
2023년 7월 18일

항상 좋은 글 감사합니다.

1개의 답글