[알고리즘] Chapter03. 알고리즘(선형 검색, 이진 검색, 순위, 버블 정렬, 삽입 정렬, 선택 정렬, 최댓값, 최솟값, 최빈값)

✍🏻 24일 공부 이야기.

알고리즘 단계로 접어들었다..!! 오늘은 선형 검색, 이진 검색, 순위, 버블 정렬, 삽입 정렬, 선택 정렬, 최댓값, 최솟값, 최빈값에 대해 공부했다:)

알고리즘이란, 어떠한 문제를 풀기 위해 정해진 일련의 절차나 방법을 공식화한 형태를 뜻한다.

선형 검색

• 선형 검색 : 선형으로 나열되어 있는 데이터를 순차적으로 스캔하면서 원하는 값을 찾아냄. (검색 성공 / 검색 실패)

datas = [3,2,5,7,9,1,0,8,6,4]
print(f'datas : {datas}')
print(f'datas length : {len(datas)}')

searchData = int(input("찾으려는 숫자 입력 : "))
searchResultIdx = -1

n = 0
while True:
  #찾으려는 값이 있다면 len(datas) - 1 이하 인덱스에서 검색되어야함
  if n == len(datas): #따라서 n이 len(datas)까지 갔다는 것은 찾으려는 값이 없다는 것을 의미
    searchResultIdx = -1
    break
  elif datas[n] == searchData: #찾으려는 값이 검색되었다면
    searchResultIdx = n #해당 인덱스를 출력
    break
  n += 1

print(f'searchResultIdx : {searchResultIdx}')

💻출력

datas : [3, 2, 5, 7, 9, 1, 0, 8, 6, 4]
datas length : 10
찾으려는 숫자 입력 : 9
searchResultIdx : 4

• 보초법 : 마지막 인덱스에 찾으려는 값을 추가해서 찾는 과정. (지막 이전에 찾으려는 값이 검색되면 검색 성공 / 마지막에 찾으려는 값이 검색되면 검색 실패)

datas = [3,2,5,7,9,1,0,8,6,4]
print(f'datas : {datas}')
print(f'datas length : {len(datas)}')

searchData = int(input("찾으려는 숫자 입력 : "))
searchResultIdx = -1

datas.append(searchData) #(a)

n = 0
while True:
  if datas[n] == searchData: #n 인덱스에서 찾으려는 값이 검색됨
    if n != len(datas) -1 : #만약 n이 (a)에서 내가 추가한 값의 인덱스가 아니라면 
      searchResultIdx = n #해당 인덱스가 찾고자하는 인덱스임
    break
  n += 1 #값이 검색이 안되었다면, 다음 인덱스로 넘어

print(f'datas : {datas}')
print(f'datas length : {len(datas)}')
print(f'searchResultIdx : {searchResultIdx}')

💻 출력

datas : [3, 2, 5, 7, 9, 1, 0, 8, 6, 4]
datas length : 10
찾으려는 숫자 입력 : 10
datas : [3, 2, 5, 7, 9, 1, 0, 8, 6, 4, 10]
datas length : 11
searchResultIdx : -1

이진 검색

• 이진 검색 : 정렬되어 있는 자료구조에서 중앙값과의 크고 작음을 이용해서 데이터를 검색함.

  정렬된 자료구조에서 찾고자하는 값과 중앙값을 비교했을 때,
  찾고자하는 값이 중앙값보다 크다면 -> 중앙값 기준 오른쪽에서 더 비교하면 되고
  찾고자하는 값이 중앙값보다 작다면 -> 중앙값 기준 왼쪽에서 비교하면 됨.

  👀 데이터의 개수가 짝수인 경우, 나머지는 버림 처리함. (아래 코드 설명 참고)

datas = [3,2,5,7,9,1,0,8,6,4]
print(f'datas : {datas}')
print(f'datas length : {len(datas)}')

searchData = int(input("찾으려는 숫자 입력 : "))
searchResultIdx = -1

datas.sort() #나중에 정렬 모듈도 만들어볼 것임.
print(f'datas sort : {datas}')
staIdx = 0
endIdx = len(datas) - 1
'''
위 예제를 보면,
시작 인덱스 : 0 , 마지막 인덱스 : 9이므로
중간 인덱스(midIdx) : 4.5가 나온다.
중앙값을 정할 때, 데이터의 개수가 짝수인 경우 나머지는 버림 처리 하므로
print(midVal) 을 해보면 datas[4] = 4 가 나오는 것을 확인할 수 있다. 
'''
midIdx = (staIdx + endIdx) // 2 
midVal = datas[midIdx]

#찾고자하는 값이 첫번째 인덱스 값 이상, 마지막 인덱스 값 이하일때
#즉 리스트 내에 값이 있는 경우에만 값을 찾음.  
while searchData <= datas[len(datas)-1] and searchData >= datas[0]:
  if searchData > midVal: #찾으려는 값이 중앙값보다 우측에 있는 경우
    staIdx = midIdx #처음값을 중앙값으로 대체하고 
    midIdx = (staIdx + endIdx) // 2 #다시 중앙값을 계산해 반복
    midVal = datas[midIdx]
    print(f'midIdx : {midIdx}')
    print(f'midVal : {midVal}')
  elif searchData < midVal: #찾으려는 값이 중앙값보다 좌측에 있는 경우
    endIdx = midIdx #마지막 값을 중앙값으로 대체하고
    midIdx = (staIdx + endIdx) // 2 #다시 중앙값을 계산해 반복
    midVal = datas[midIdx]
    print(f'midIdx : {midIdx}')
    print(f'midVal : {midVal}')
  elif searchData == midVal: #중앙값이 찾으려는 값인 경우
    searchResultIdx = midIdx #해당 인덱스 출력 
    break
print(f'searchResultIdx : {searchResultIdx}')

💻 출력

datas : [3, 2, 5, 7, 9, 1, 0, 8, 6, 4]
datas length : 10
찾으려는 숫자 입력 : 5
datas sort : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
midIdx : 6
midVal : 6
midIdx : 5
midVal : 5
searchResultIdx : 5

순위

• 순위 : 수의 크고 작음을 이용해서 수의 순서를 정함.

import random

nums = random.sample(range(50,101), 20)
ranks = [0 for i in range(20)]

print(f'nums : {nums}')
print(f'ranks : {ranks}')

#rank가 작을수록 큰 값이라 할 때
for idx, num1 in enumerate(nums): #인덱스와 값에 모두 접근 가능한 enumerate
  for num2 in nums:
    if num1 < num2 : #num1보다 num2의 값이 작다면
      ranks[idx] += 1 #num1의 rank는 하나 더해짐

print(f'nums : {nums}')
print(f'ranks : {ranks}')

for idx, num in enumerate(nums):
  print(f'nums : {num} \t rank : {ranks[idx]}')

💻 출력

버블 정렬

• 버블 정렬 : 처음부터 끝까지 인접하는 인덱스의 값을 순차적으로 비교하면서 큰 숫자를 가장 끝으로 옮기는 알고리즘.

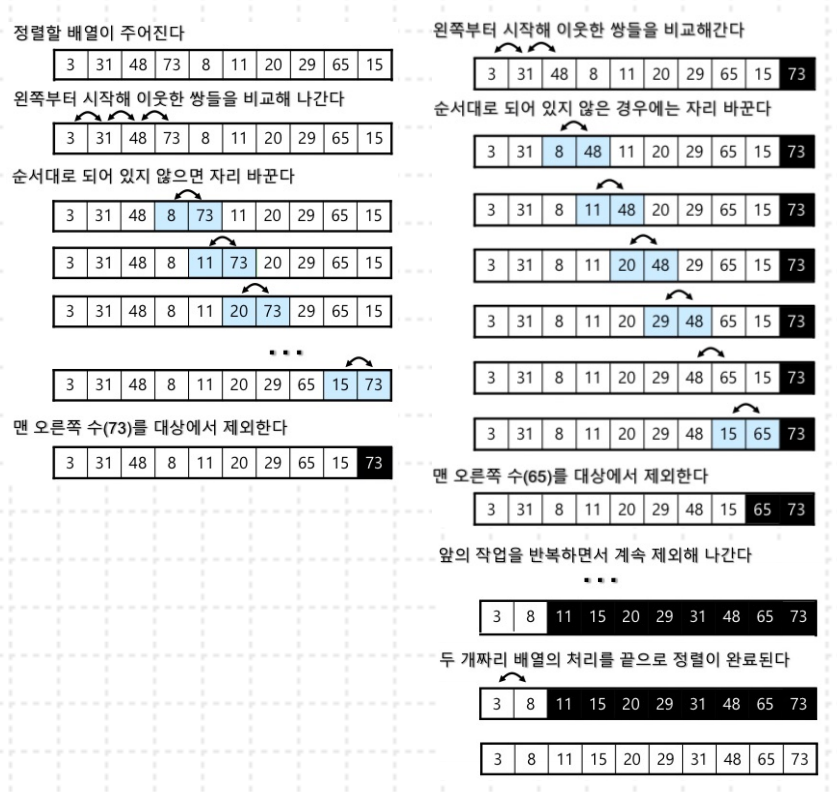
nums = [10,21,7,2,0]
print(f'not sorted nums : {nums}')

length = len(nums)-1 #아래 코드에서 인덱스 j와 j+1을 비교하므로 -1을 해줘야함
                     #len(nums)는 out of range 에러 뜸!
for i in range(length):
  # print('***************')
  # print(f'i : {i}')
  for j in range(length - i): #처음부터 끝까지 비교하면 결국 큰 값은 맨 뒤에 있으므로
                              #리스트의 길이 중 i 만큼은 이미 정렬이 된 상태라고 볼 수 있음
                              #그래서 length - i 전까지만 비교해주면 됨.  
    # print(f'j : {j}')
    # print(f'nums[j] : {nums[j]}')
    # print(f'nums[j+1] : {nums[j+1]}')
    if nums[j] > nums[j+1]:
      nums[j] , nums[j+1] = nums[j+1], nums[j] 
    print(nums)
print(f'sorted nums : {nums}')

💻 출력
not sorted nums : [10, 21, 7, 2, 0][10, 21, 7, 2, 0]
[10, 7, 21, 2, 0][10, 7, 2, 21, 0]
[10, 7, 2, 0, 21][7, 10, 2, 0, 21]
[7, 2, 10, 0, 21][7, 2, 0, 10, 21]
[2, 7, 0, 10, 21][2, 0, 7, 10, 21]
[0, 2, 7, 10, 21]
sorted nums : [0, 2, 7, 10, 21]

import copy

def bubbleSort(ns, deepCopy = True):
  #기존의 정렬 전인 리스트를 보존하고 싶을때 복사를 해줘야한다.
  '''
  아래에 설명해두겠지만, deepcopy를 사용해주어야 찐 깊은 복사이다.
  '''
  if deepCopy:
    cns = copy.copy(ns)
  else:
    cns = ns
  #버블 정렬
  length = len(cns) -1
  for i in range(length):
    for j in range(length -i):
      if cns[j] > cns[j+1]:
        cns[j], cns[j+1] = cns[j+1], cns[j]
  return cns
  
  
  
import random

students = []
for i in range(20):
  students.append(random.randint(171.,185))

print(f'students : {students}')
sortedStudents = bubbleSort(students)

print(f'students : {students}')
print(f'sorted students : {sortedStudents}')

💻 출력

students : [177, 179, 178, 183, 178, 180, 177, 174, 175, 176, 173, 178, 173, 177, 180, 173, 172, 177, 181, 178]
students : [177, 179, 178, 183, 178, 180, 177, 174, 175, 176, 173, 178, 173, 177, 180, 173, 172, 177, 181, 178]
sorted students : [172, 173, 173, 173, 174, 175, 176, 177, 177, 177, 177, 178, 178, 178, 178, 179, 180, 180, 181, 183]

원본 데이터를 보존하기 위해 copy를 사용했다. 이전에도 얕은 복사/깊은 복사와 관련해서 🖱️포스팅한 적 있지만, 또 헷갈린다... 🤯 강사님께서는 copy()를 깊은 복사라 하시고 정말 결과 자체도 깊은 복사와 같이 나와서 또 다시 혼자서 이것저것 만져보다가 알아냈다ㅋㅋㅋ..

2차원 이상의 리스트가 아니여서 위 문제에선 copy()깊은 복사처럼 보이는 것일뿐.. 얕은 복사이다:) 지금은 students , sortedStudents 변수들의 주소를 봐도 다르게 나와서 깊은 복사처럼 보이지만 만약 2차원 이상의 리스트 값들이 있었다면 그 값은 주소가 같았을 것이다.

이해하는데에 도움을 줬던 링크도 같이 첨부할게요!
🖱️ 코드로 이해하기
🖱️ 그림으로 이해하기

삽입 정렬

• 삽입 정렬 : 정렬되어 있는 자료 배열과 비교해서, 정렬 위치를 찾는 알고리즘.
  

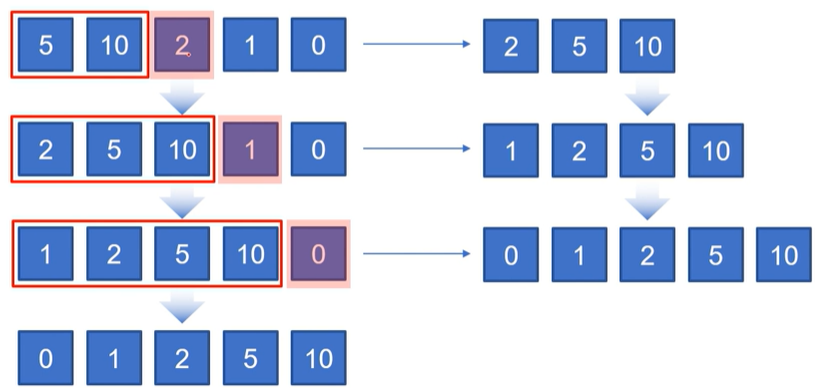
nums = [5,10,2,1,0]

for i1 in range(1, len(nums)):#인덱스 1부터 시작해서 비교하면 됨
  # print(f'i1 : {i1}')
  i2 = i1 -1 #앞서 정렬된 값의 인덱스
  cNum = nums[i1]
  #print(f'i2 : {i2} , cNums : {nums[i1]}')

  while nums[i2] > cNum and i2 >= 0: 
    #print(f'i2 : {i2} , nums[i2] : {nums[i2]}')
    #현재 왼쪽에 정렬되어있는 숫자보다 cNum이 작다면(정상적인 인덱스 범위에는 당연히 있어야함)
    nums[i2 + 1] = nums[i2] #nums[i2]가 더 큰 값이므로 오른쪽으로 한 칸씩 옮김
    #print(f'sorted nums : {nums}')
    i2 -= 1 #왼쪽에 정렬되어있는 값들 중에 삽입해야할 위치가 있는지 찾아보기 위함
  nums[i2 + 1] = cNum #삽입해야할 위치에 값 넣기
  print(f'{i1} term sorted nums : {nums}')

print(f'finally sorted nums : {nums}')  

💻 출력

1 term sorted nums : [5, 10, 2, 1, 0]
2 term sorted nums : [2, 5, 10, 1, 0]
3 term sorted nums : [1, 2, 5, 10, 0]
4 term sorted nums : [0, 1, 2, 5, 10]
finally sorted nums : [0, 1, 2, 5, 10]

선택 정렬

• 선택 정렬 : 주어진 리스트 중에 최소값을 찾아, 그 값을 맨 앞에 위치한 값과 교체하는 방식으로 자료를 정렬하는 알고리즘.

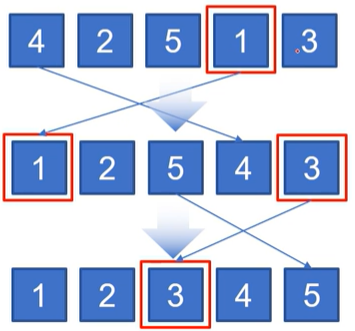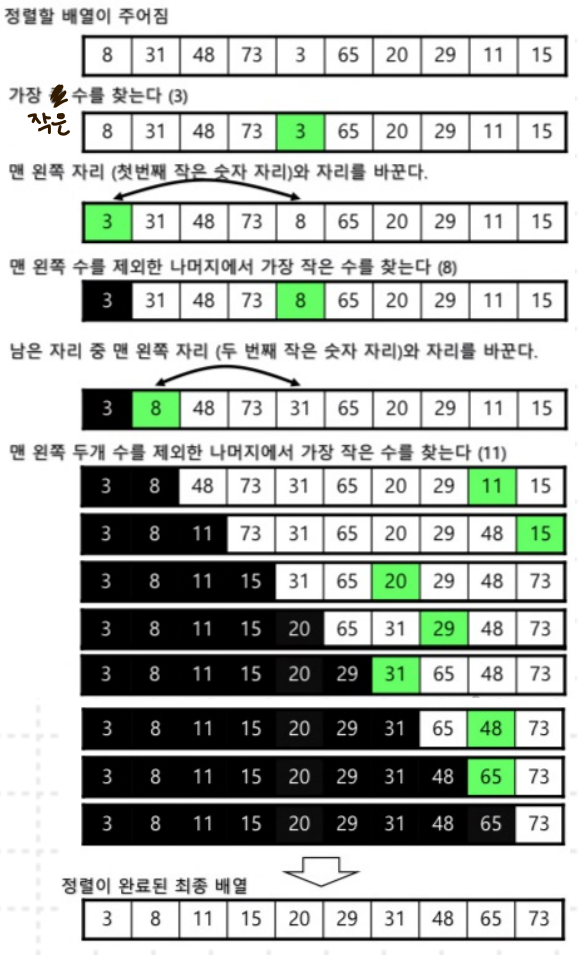nums = [4,2,5,1,3]
print(f'nums : {nums}')

for i in range(len(nums) - 1):
  minIdx = i #최소값 위치(기준)

  #정렬이 된 왼쪽 원소들은 제외하고 최소값을 찾기 위한 for문
  for j in range(i + 1, len(nums)):  
    if nums[j] < nums[minIdx]:
      minIdx = j

  #맨 왼쪽의 값과 최소값을 교체
  nums[i], nums[minIdx] = nums[minIdx], nums[i]
  print(f'sorted nums : {nums}')

💻 출력

nums : [4, 2, 5, 1, 3]
sorted nums : [1, 2, 5, 4, 3]
sorted nums : [1, 2, 5, 4, 3]
sorted nums : [1, 2, 3, 4, 5]
sorted nums : [1, 2, 3, 4, 5]

최대값 & 최소값 & 최빈값

api를 사용하지 않고 구해보기 !

• 최대값 : 자료구조에서 가장 큰 값
• 최소값 : 자료구조에서 가장 작은 값
• 최빈값 : 자료구조에서 빈도수가 가장 많은 값

최대값

#최대값(숫자.ver)
class MaxAlgorithm:
  def __init__(self, n):
    self.nums = n
    self.maxNum = 0

  def getMaxNum(self):
    self.maxNum = self.nums[0]

    for n in self.nums:
      if self.maxNum < n: #n이 더 큰 숫자이면
        self.maxNum = n #최대값은 n
    return self.maxNum
    
maxnum_list = MaxAlgorithm([-2,-4,5,7,10,0,8,20,-11])
maxNum = maxnum_list.getMaxNum()
print(f'maxNum : {maxNum}')
#maxNum : 20

#최대값(문자.ver)
#문자열을 아스키코드로 변환해주는 함수 : ord()

class MaxCharAlgorithm:
  def __init__(self, c):
    self.chars = c
    self.maxChar = 0

  def getMaxChar(self):
    self.maxChar = self.chars[0]

    for c in self.chars:
      if ord(self.maxChar) < ord(c): 
        self.maxChar = c 
    return self.maxChar
    
maxchar_list = MaxCharAlgorithm(['c', 'x', 'Q', 'A', 'e'])
maxChar = maxchar_list.getMaxChar()
print(f'maxChar : {maxChar}')
#maxChar : x

최소값

#최소값(숫자.ver)
class MinAlgorithm:
  def __init__(self, n):
    self.nums = n
    self.minNum = 0

  def getMinNum(self):
    self.minNum = self.nums[0]

    for n in self.nums:
      if self.minNum > n: 
        self.minNum = n 
    return self.minNum
    
minnum_list = MinAlgorithm([-2,-4,5,7,10,0,8,20,-11])
minNum = minnum_list.getMinNum()
print(f'minNum : {minNum}')
#minNum : -11

#최소값(문자.ver)
class MinCharAlgorithm:
  def __init__(self, c):
    self.chars = c
    self.minChar = 0

  def getMinChar(self):
    self.minChar = self.chars[0]

    for c in self.chars:
      if ord(self.minChar) > ord(c): 
        self.minChar = c 
    return self.minChar


minchar_list = MinCharAlgorithm(['c', 'x', 'Q', 'A', 'e'])
minChar = minchar_list.getMinChar()
print(f'minChar : {minChar}')
#minChar : A

최빈값

'''
#### 최빈값 알고리즘 ####
최대값의 크기를 길이로 가진 0 리스트(indexes)가 있다.
최빈값을 찾고자 하는 리스트(nums)를 훑으며
nums 원소들의 값에 해당하는 indexes 인덱스 값에 1씩 더해주면
최종적으로 indexes의 최대값의 인덱스가 nums의 최빈값이 된다.
'''
class MaxAlgorithm:
  def __init__(self, n):
    self.nums = n
    self.maxNum = 0 
    self.maxNumIdx = 0

  def setMaxIdxAndNum(self): #최대값과 그의 인덱스 찾기
    self.maxNum = self.nums[0]
    self.maxNumIdx = 0

    for i, n in enumerate(self.nums):
      if self.maxNum < n:
        self.maxNum = n
        self.maxNumIdx = i
  def getMaxNum(self): #최대값
    return self.maxNum

  def getMaxNumIdx(self): #최대값의 인덱스
    return self.maxNumIdx


#구하고자 하는 nums 리스트
nums = [1,3,7,6,7,7,7,12,12,17]
maxnum_list = MaxAlgorithm(nums)
maxnum_list.setMaxIdxAndNum()
maxNum = maxnum_list.getMaxNum()
print(f'nums\'s maxNum for len(indexes)  : {maxNum}')

indexes = [0 for i in range(maxNum + 1)]
print(f'indexes : {indexes}')

#최빈값 구하는 부분
for n in nums:
  indexes[n] = indexes[n] + 1

print(f'mode indexes : {indexes}')

'''
최빈값이 들어있는 indexes 리스트의 최대값 인덱스 찾기
'''
maxAlo = MaxAlgorithm(indexes)
maxAlo.setMaxIdxAndNum()
maxNum = maxAlo.getMaxNum() #빈도수(indexes의 최대값에 해당)
maxNumIdx = maxAlo.getMaxNumIdx() #최빈값(indexes의 최대값 인덱스에 해당)
print(f'indexes\'s maxNum : {maxNum}')
print(f'indexes\'s maxNumIdx : {maxNumIdx}')

print(f'즉, {maxNumIdx}의 빈도수가 {maxNum}로 가장 높다.')

💻 출력

nums's maxNum for len(indexes) : 17
indexes : [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
mode indexes : [0, 1, 0, 1, 0, 0, 1, 4, 0, 0, 0, 0, 2, 0, 0, 0, 0, 1]
indexes's maxNum : 4
indexes's maxNumIdx : 7
즉, 7의 빈도수가 4로 가장 높다.